6. Recursion exercise
02 Jun 2020 | Algorithm
Sum of Natural Number using Recursion
#include <stdio.h>
int sum(int n) // recursive method
{
if(n==0)
return 0;
return sum(n-1)+n; // n
}
int Isum(int n) // for loop method
{
int s=0,i; // 1
for(i=1;i<=n;i++) // n+1
s=s+i; // n
return s; // 1
}
int main()
{
int r=sum(5);
printf("%d ",r);
return 0;
}
- sum(n) = 1+2+3+4+…(n-1) +n
- sum(n) = (n-1)+n
- 조건
- n=0, sum(n) = 0
- n>0, sum(n) = (n-1)+n
- Time Complexity = O(n)
Factorial
#include <stdio.h>
int fact(int n)
{
if(n==0)
return 1;
return fact(n-1) * n;
}
int Ifact(int n)
{
int f=1,i;
for(i=1;i<=n;i++)
f=f * i;
return f;
}
int main()
{
int r=fact(5);
printf("%d ",r);
return 0;
}
- Sum 하고 똑같은 방식이다.
Power(Exponent)
#include <stdio.h>
int power(int m,int n)
{
if(n==0)
return 1;
return power(m,n-1) * m;
}
int power1(int m,int n)
{
if(n==0)
return 1;
if(n%2==0)
return power1(m*m,n/2);
return m * power1(m*m,(n-1)/2);
}
int main()
{
int r=power1(9,3);
printf("%d ",r);
return 0;
}
- pow(m,n) = (mM….* (n-1)) * m
- pow(m,n) = pow(m,n-1) * m
- 조건
- n = 0, p(m,n) = 1;
- n>0, p(m,n) = p(m,n-1)* m
Talyor Series using static variable
#include <stdio.h>
double e(int x, int n)
{
static double p=1,f=1;
double r;
if(n==0)
return 1;
r=e(x,n-1);
p=p*x;
f=f*n;
return r+p/f;
}
int main()
{
printf("%lf \n",e(4,4));
return 0;
}
- time complexity = n(n+1) = O(n)
Talyor Series Horner’s Rule
double e(int x, int n)
{
static double s;
if(n==0)
return s;
s=1+x*s/n;
return e(x,n-1);
}
int main()
{
printf("%lf \n",e(2,10));
return 0;
}
- tail recursive 방법을 써서 구하는 방식, 즉 전에 방법하고 반대로 되는 방식이다.
Taylor Series Iterative
#include <stdio.h>
double e(int x, int n)
{
double s=1;
int i;
double num=1;
double den=1;
for(i=1;i<=n;i++)
{
num*=x;
den*=i;
s+=num/den;
}
return s;
}
int main()
{
printf("%lf \n",e(1,10));
return 0;
}
- for loop를 사용하여 구현하는 방법
Fibonacci Series
- Fibonacci Series 개념
- fin(n)=(n-2)+(n-1)
- 즉, 0 1 1 2 3 5 8 13 18 31 …. 이런 식으로 늘려나가는 것
#include <stdio.h>
int fib(int n) // for loop 방법
{
int t0=0,t1=1,s=0,i;
if(n<=1) return n;
for(i=2;i<=n;i++)
{
s=t0+t1;
t0=t1;
t1=s;
}
return s;
}
int rfib(int n) // recursive 방법
{
if(n<=1)return n;
return rfib(n-2)+rfib(n-1);
}
int F[10];
int mfib(int n)
{
if(n<=1)
{
F[n]=n;
return n;
}
else
{
if(F[n-2]==-1)
F[n-2]=mfib(n-2);
if(F[n-1]==-1)
F[n-1]=mfib(n-1);
F[n]=F[n-2]+F[n-1];
return F[n-2]+F[n-1];
}
}
int main()
{
int i;
for(i=0;i<10;i++)
F[i]=-1;
printf("%d \n",mfib(5));
return 0;
}
- 조건
- n=0, fin(n) = 0;
- n=1, fin(n) = 1;
- n>1, fin(n) = fin(n-2) + fib(n-1)
- Time Complexity = O(2^n)
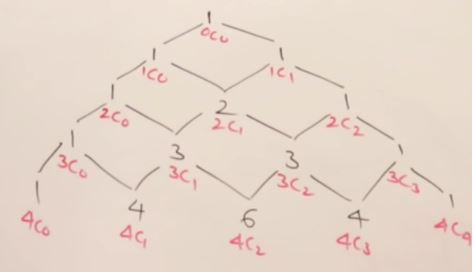
nCr using Recursion(Combination Formular)
#include <stdio.h>
int fact(int n)
{
if(n==0)return 1;
return fact(n-1) * n;
}
int nCr(int n,int r)
{
int num,den;
num=fact(n);
den=fact(r) * fact(n-r);
return num/den;
}
int NCR(int n,int r)
{
if(n==r || r==0)
return 1;
return NCR(n-1,r-1)+NCR(n-1,r);
}
int main()
{
printf("%d \n",NCR(5,3));
return 0;
}
- Time Complexity O(n)
Tower of Hanoi
- “1” is from
- “2” is waiting
- “3” is to
#include <stdio.h>
void TOH(int n,int A,int B,int C)
{
if(n>0)
{
TOH(n-1,A,C,B);
printf("(%d,%d)\n",A,C);
TOH(n-1,B,A,C);
}
}
int main()
{
TOH(3,1,2,3);
return 0;
}
- Time Complexity = 1 + 2 + 2^2 + … +2^n = 2^(n+1) - 1 = O(2^(n+1))
Sum of Natural Number using Recursion
#include <stdio.h>
int sum(int n) // recursive method
{
if(n==0)
return 0;
return sum(n-1)+n; // n
}
int Isum(int n) // for loop method
{
int s=0,i; // 1
for(i=1;i<=n;i++) // n+1
s=s+i; // n
return s; // 1
}
int main()
{
int r=sum(5);
printf("%d ",r);
return 0;
}
- sum(n) = 1+2+3+4+…(n-1) +n
- sum(n) = (n-1)+n
- 조건
- n=0, sum(n) = 0
- n>0, sum(n) = (n-1)+n
- Time Complexity = O(n)
Factorial
#include <stdio.h>
int fact(int n)
{
if(n==0)
return 1;
return fact(n-1) * n;
}
int Ifact(int n)
{
int f=1,i;
for(i=1;i<=n;i++)
f=f * i;
return f;
}
int main()
{
int r=fact(5);
printf("%d ",r);
return 0;
}
- Sum 하고 똑같은 방식이다.
Power(Exponent)
#include <stdio.h>
int power(int m,int n)
{
if(n==0)
return 1;
return power(m,n-1) * m;
}
int power1(int m,int n)
{
if(n==0)
return 1;
if(n%2==0)
return power1(m*m,n/2);
return m * power1(m*m,(n-1)/2);
}
int main()
{
int r=power1(9,3);
printf("%d ",r);
return 0;
}
- pow(m,n) = (mM….* (n-1)) * m
- pow(m,n) = pow(m,n-1) * m
- 조건
- n = 0, p(m,n) = 1;
- n>0, p(m,n) = p(m,n-1)* m
Talyor Series using static variable
#include <stdio.h>
double e(int x, int n)
{
static double p=1,f=1;
double r;
if(n==0)
return 1;
r=e(x,n-1);
p=p*x;
f=f*n;
return r+p/f;
}
int main()
{
printf("%lf \n",e(4,4));
return 0;
}
- time complexity = n(n+1) = O(n)
Talyor Series Horner’s Rule
double e(int x, int n)
{
static double s;
if(n==0)
return s;
s=1+x*s/n;
return e(x,n-1);
}
int main()
{
printf("%lf \n",e(2,10));
return 0;
}
- tail recursive 방법을 써서 구하는 방식, 즉 전에 방법하고 반대로 되는 방식이다.
Taylor Series Iterative
#include <stdio.h>
double e(int x, int n)
{
double s=1;
int i;
double num=1;
double den=1;
for(i=1;i<=n;i++)
{
num*=x;
den*=i;
s+=num/den;
}
return s;
}
int main()
{
printf("%lf \n",e(1,10));
return 0;
}
- for loop를 사용하여 구현하는 방법
Fibonacci Series
- Fibonacci Series 개념
- fin(n)=(n-2)+(n-1)
- 즉, 0 1 1 2 3 5 8 13 18 31 …. 이런 식으로 늘려나가는 것
#include <stdio.h>
int fib(int n) // for loop 방법
{
int t0=0,t1=1,s=0,i;
if(n<=1) return n;
for(i=2;i<=n;i++)
{
s=t0+t1;
t0=t1;
t1=s;
}
return s;
}
int rfib(int n) // recursive 방법
{
if(n<=1)return n;
return rfib(n-2)+rfib(n-1);
}
int F[10];
int mfib(int n)
{
if(n<=1)
{
F[n]=n;
return n;
}
else
{
if(F[n-2]==-1)
F[n-2]=mfib(n-2);
if(F[n-1]==-1)
F[n-1]=mfib(n-1);
F[n]=F[n-2]+F[n-1];
return F[n-2]+F[n-1];
}
}
int main()
{
int i;
for(i=0;i<10;i++)
F[i]=-1;
printf("%d \n",mfib(5));
return 0;
}
- 조건
- n=0, fin(n) = 0;
- n=1, fin(n) = 1;
- n>1, fin(n) = fin(n-2) + fib(n-1)
- Time Complexity = O(2^n)
nCr using Recursion(Combination Formular)
#include <stdio.h>
int fact(int n)
{
if(n==0)return 1;
return fact(n-1) * n;
}
int nCr(int n,int r)
{
int num,den;
num=fact(n);
den=fact(r) * fact(n-r);
return num/den;
}
int NCR(int n,int r)
{
if(n==r || r==0)
return 1;
return NCR(n-1,r-1)+NCR(n-1,r);
}
int main()
{
printf("%d \n",NCR(5,3));
return 0;
}
- Time Complexity O(n)
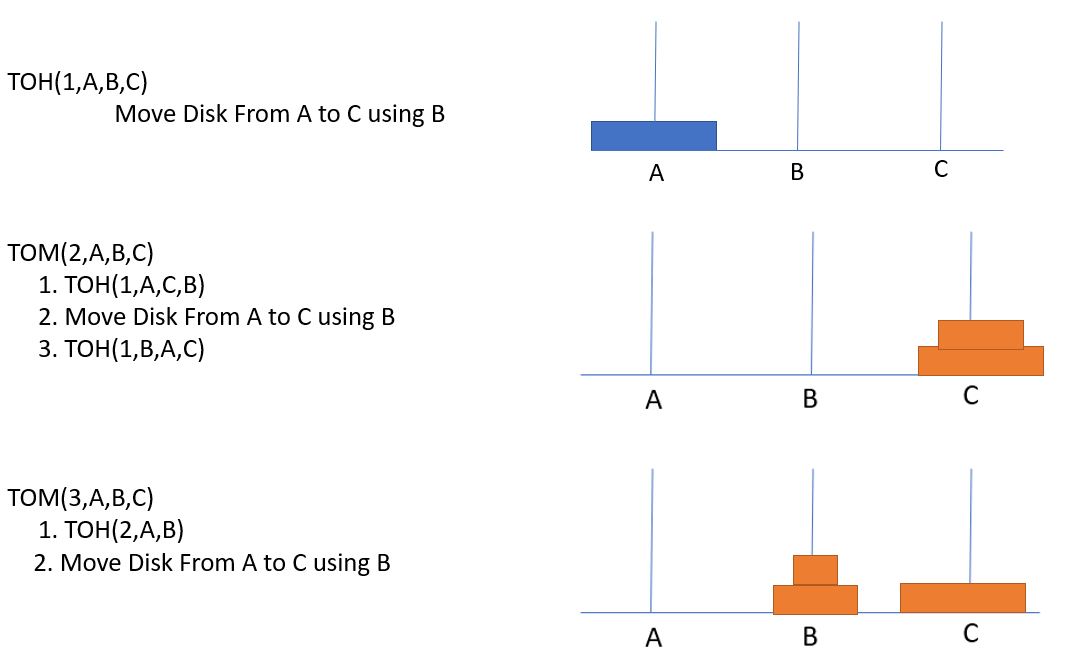
Tower of Hanoi
- “1” is from
- “2” is waiting
- “3” is to
#include <stdio.h>
void TOH(int n,int A,int B,int C)
{
if(n>0)
{
TOH(n-1,A,C,B);
printf("(%d,%d)\n",A,C);
TOH(n-1,B,A,C);
}
}
int main()
{
TOH(3,1,2,3);
return 0;
}
- Time Complexity = 1 + 2 + 2^2 + … +2^n = 2^(n+1) - 1 = O(2^(n+1))
















Comments