8. Array ADT
02 Jun 2020 | Algorithm
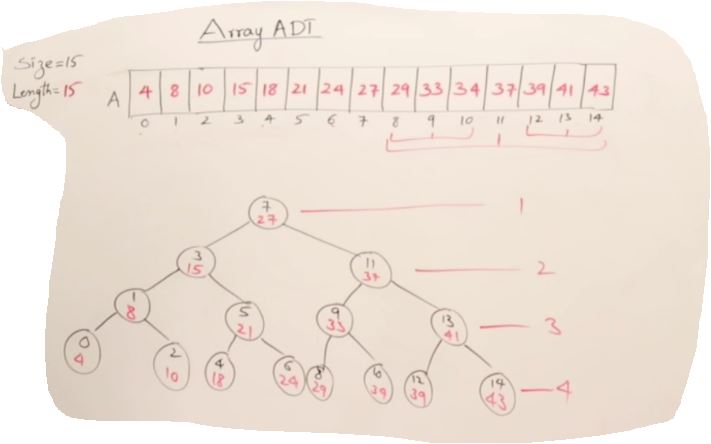
Array Abstract Data type (ADT)
- Data
- Array space
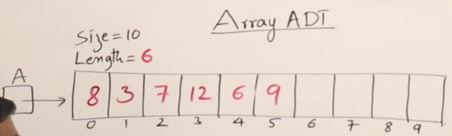
- size
- Length(number of element)
- Operation
- Display()
for (int i=0; i<length; i++)
{
cout<<A[i]<<endl;
}
- Add(x)/Append(x)
A[length] = x;
Length++;
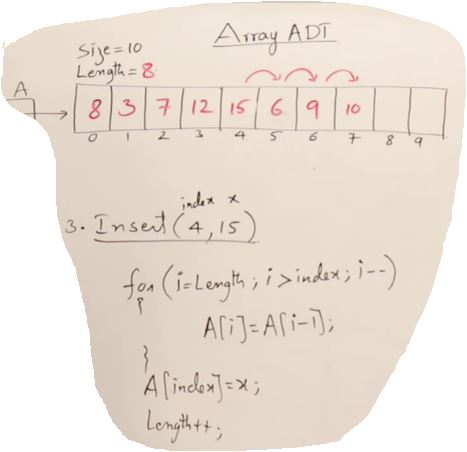
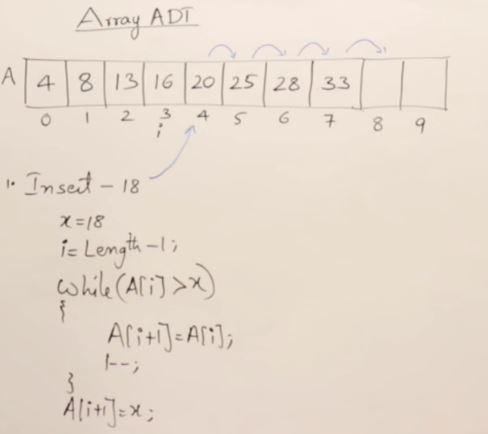
- Insert(index, x)
for (i=length; i > index; i--){
A[i] = A[i-1];
}
A[length] = x;
length ++;
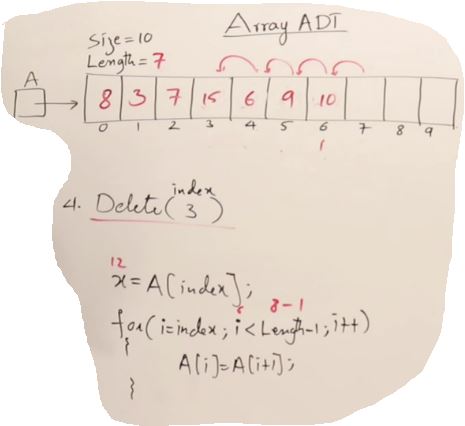
- Delete(index)
void delet(int index)
{
int x = A[index];
for (int i = index; i<Length-1; i++)
{
A[i] = A[i+1];
}
}
- Search(x)
- Linear Search
- Binary Search
int binsearch(int l,int r,int key)
{
int mid = (l+r)/2;
if(l=<r)
{
if(A[mid]==key)
{
return mid;
}
else if(key<A[mid])
return binsearch(l,mid-1,key);
else
return binsearch(mid+1, r,key);
}
return -1;
}
-
O(logn+1)-> O(logn)
- Get(index)
int get(int index)
{
if(index>=0 && index<length)
{
return A[index];
}
}
- Set(index, x)
set(index,x)
{
if(index>=0 && index<length)
{
A[index]=x;
}
}
- max()/min()
int max()
{
max = A[0];
for(int i = 1; i<length; i++1)
{
if(A[i]>max)
max=A[i];
}
return max;
}
- Reverse()
for(int i=0, j=Length-1;i<j; i++, j--)
{
temp=A[i];
A[i] = A[j]
A[j] = temp;
}
- switch()/rotate()
for (i=0; i<length; i++)
{
if(key==A[i])
{
swap(A[i],A[i-1])
return i-1;
}
}
- sorted
bool isSorted(int[] A, n)
{
for(int i=0; i<n-1; i++)
{
if(A[i]>A[i+1])
return false
}
return true
}
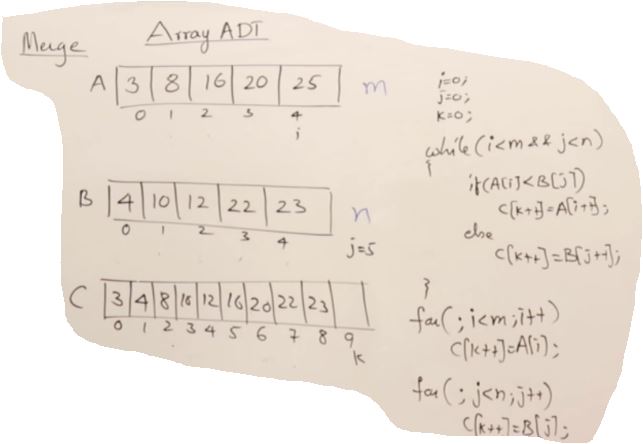
- Merge
- Append
- Concat
- compare
- copy
int i = 0;
int j = 0;
int k = 0;
while (i<m && j<n)
{
if(A[i]<B[j])
{
C[k++] = A[i++]
}
else
{
C[k++] = B[j++]
}
}
- Time Complexity O(m+n)
Array Abstract Data type (ADT)
- Data
- Array space
- size
- Length(number of element)
- Operation
- Display()
for (int i=0; i<length; i++)
{
cout<<A[i]<<endl;
}
- Add(x)/Append(x)
A[length] = x;
Length++;
- Insert(index, x)
for (i=length; i > index; i--){
A[i] = A[i-1];
}
A[length] = x;
length ++;
- Delete(index)
void delet(int index)
{
int x = A[index];
for (int i = index; i<Length-1; i++)
{
A[i] = A[i+1];
}
}
- Search(x)
- Linear Search
- Binary Search
int binsearch(int l,int r,int key)
{
int mid = (l+r)/2;
if(l=<r)
{
if(A[mid]==key)
{
return mid;
}
else if(key<A[mid])
return binsearch(l,mid-1,key);
else
return binsearch(mid+1, r,key);
}
return -1;
}
-
O(logn+1)-> O(logn)
- Get(index)
int get(int index)
{
if(index>=0 && index<length)
{
return A[index];
}
}
- Set(index, x)
set(index,x)
{
if(index>=0 && index<length)
{
A[index]=x;
}
}
- max()/min()
int max()
{
max = A[0];
for(int i = 1; i<length; i++1)
{
if(A[i]>max)
max=A[i];
}
return max;
}
- Reverse()
for(int i=0, j=Length-1;i<j; i++, j--)
{
temp=A[i];
A[i] = A[j]
A[j] = temp;
}
- switch()/rotate()
for (i=0; i<length; i++)
{
if(key==A[i])
{
swap(A[i],A[i-1])
return i-1;
}
}
- sorted
bool isSorted(int[] A, n)
{
for(int i=0; i<n-1; i++)
{
if(A[i]>A[i+1])
return false
}
return true
}
- Merge
- Append
- Concat
- compare
- copy
int i = 0;
int j = 0;
int k = 0;
while (i<m && j<n)
{
if(A[i]<B[j])
{
C[k++] = A[i++]
}
else
{
C[k++] = B[j++]
}
}
- Time Complexity O(m+n)

Comments