for Robot Artificial Inteligence

10. Array ADT represented problem solving 2

11 Jun 2020 | Algorithm

Finding Missing Elements

Method 1

int sum = 0;
for(int i = 0; i<11; i++)
{
  sum=sum+A[i];
}
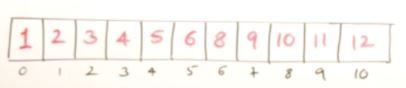
s = n*(n+1)/2 // n은 맨 마지막 element 12
int result = s - sum; // 78-71

  • 즉 expected Sum 값인 n*(n+1)/2 와 실제 Sum 값을 뺴면 빠진 Value가 뭔지 알 수 있다.

  • O(n)

Method 2

for(int = 0; i < n; i++)
{
  if(A[i]-i!=diff)
    printf(i+d)
}
  • linear search를 통해 구한다
  • 행령 element의 값과 항상 linear하게 증가하는 i의 값의 diff 값은 일정하다
  • 만약 다르다면 missing이 있다는 뜻
  • time complext O(n)

Method 3

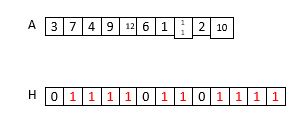
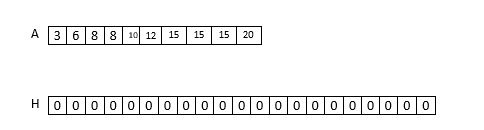
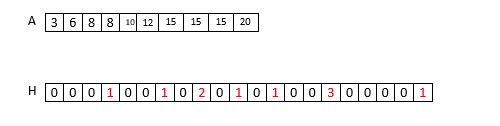
  • for loop를 사용하는게 아닌 hash table 사용하여 구하기

  • h = 12, n = 10, l=1
  • O(n)
  • array에 있는 element를 Hash table에 마크를 해서 체크(Hash table/bits)
for(int i=0; i<n; i++)
{
  H[A[i]]++;
}
for(int i = l; i<=h;i++)
{
  if(H[i]==0)
    printf("%d \n", i );
}

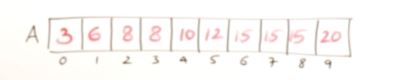
Finding Duplicate Elements

  • Finding Duplicate in sorted Array
  • Counting Duplicate in sorted Array
int n = 10;
int lastDuplicate = 0;
for(int i=0; i<n; i++)
{
  if(A[i]==A[i++] && A[i]!=lastDuplicate)
  {
    printf("(%d)\n", A[i] );
    lastDuplicate = A[i];
  }
}
  • O(n)
for(int = 0; i<n-1; i++)
{
  if(A[i]==A[i++])
  {
    j=i+1
    while(A[j]==A[i])
      j++;
    printf("%d is appearing %d times \n",A[i], j-i );
    i=j-1;
  }
}
  • O(n^2)

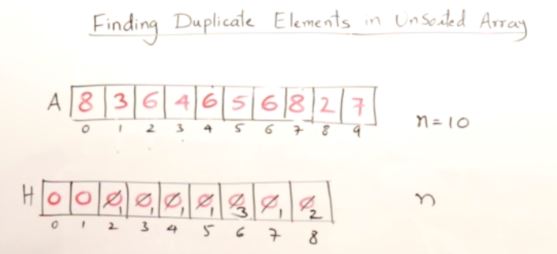
Method 2 using Hash Table

  • n = 10
for(int i=0; i<n;i++)
{
  H[A[i]]++;
}
for(int i=0; i<= max; i++)
{
  if(H[i]>1)
      printf("%d %d\n",i,H[i] );
}

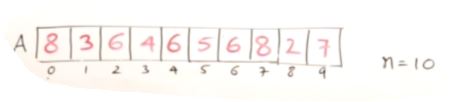
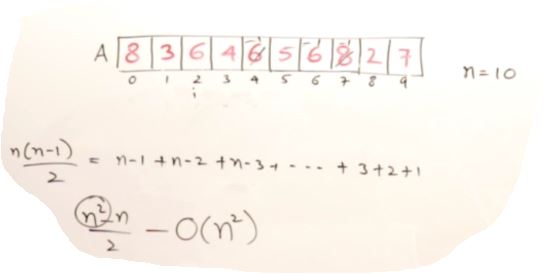
Finding Duplicate Elements in unsorted Array

  • n = 10
  • count = 1+1+1

for(int i=0; i<n-1;i++)
{
  count=1;
  if(A[i]!==-1)
  {
    for(int j=i+1; j<n;j++)
    {
      if(A[i]==A[j])
        count++;
        A[j] = -1;
    }  
  }
  if(count>1)
    printf(%d %d, A[i],count);
}

Method 2 using hash Table

Find a pair with sum k(a+b=k)

Method 2 using hash table

for(int i=0; i<n; i++)
{
  if(H[k-A[i]] ! = 0)
    printf("%d + %d = %d",A[i], k-A[i], k);
  H[A[i]]++

}

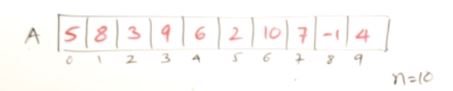
Method 3 using array table

int i =0;
int j=n-1;
while(i<j)
{
  if(A[i]+A[j]==k)
  {
    printf("%d+%d = %d", A[i], A[j],k)
    i++;
    j--;
  }
  else if (A[i]+A[j]<k)
    i++;
  else
    j--;
}
  • O(n)

Finding Max and Min in a single scan

int min = A[0];
int max = A[0];
for(i=1; i<n; i++)
{
  if(A[i]<min)
    min = A[i];
  else if (A[i]>max)
    max = A[i];
}

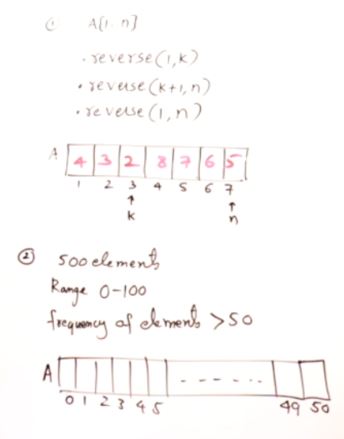
Quiz

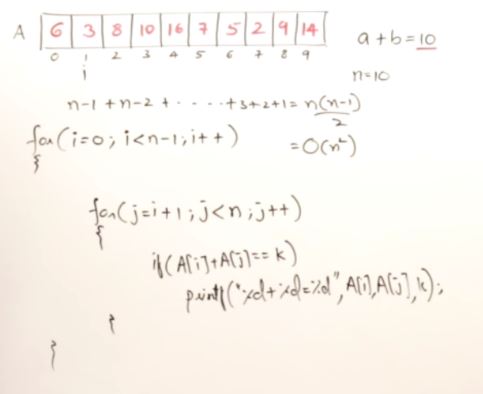
Comments