for Robot Artificial Inteligence

35. Graphs 2

26 Jun 2020 | Algorithm

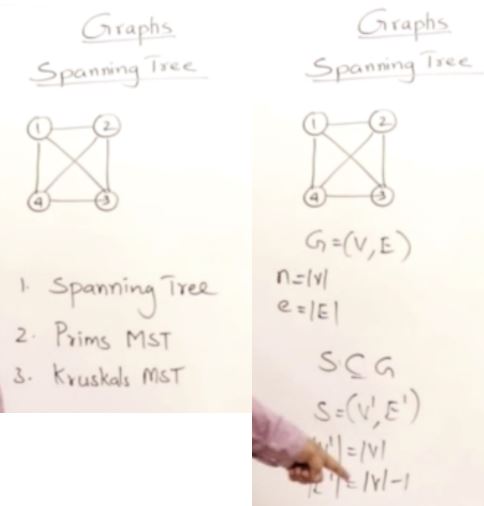
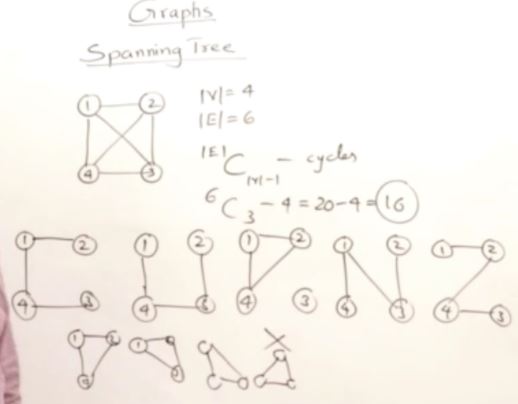
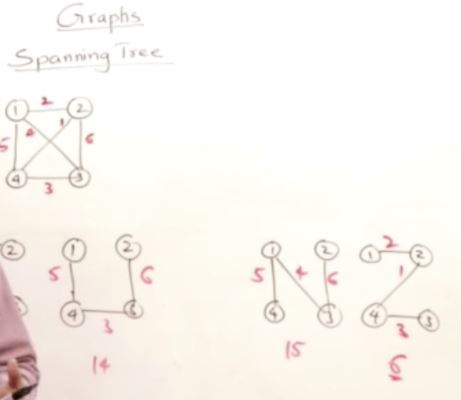
Spanning Tree

  • 16 spanning Tree
    • 즉 노드끼리 연결된 형상이 얼마나 많이 할 수 있는지 알려주는 정보

  • SPanning Tree는 어디서 사용하나? Traversal business trip 같은 곳 최단 거리 찾는 것에 사용된다.

  • 그렇다면 각 연결되어있는 Graph의 최단 거리 및 목적 값을 찾기 위해 효과적인 spanning Tree 방법이 뭐가 있는 지 보자.

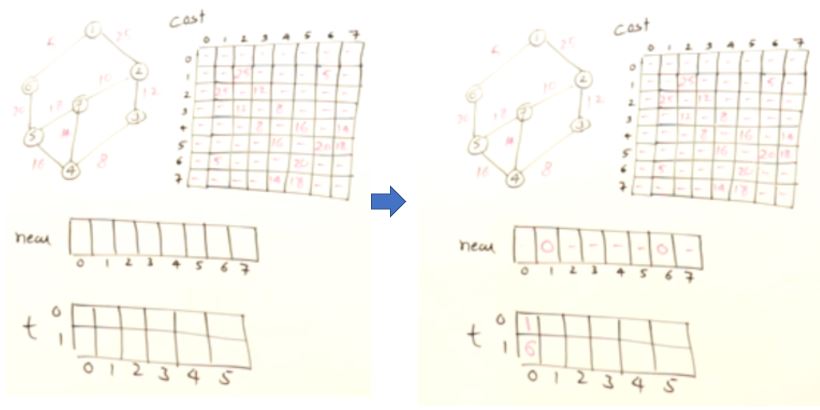
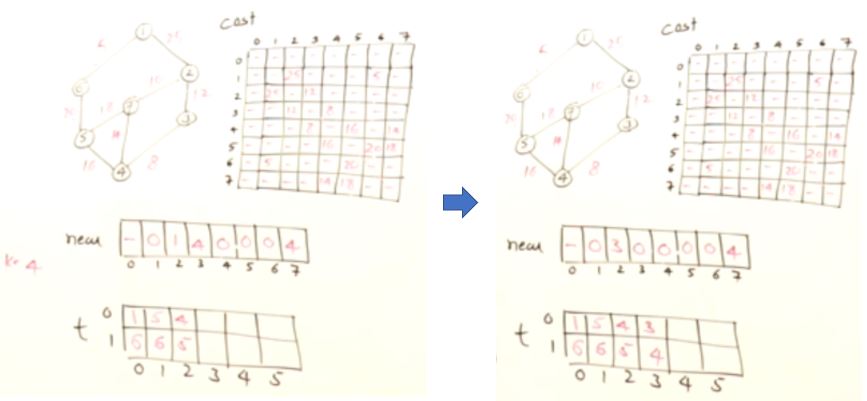
Prim’s Minimum Cost Spanning Tree

#include <iostream>
#define V 8
#define I 32767

using namespace std;

void PrintMST(int T[][V-2], int G[V][V]){
    cout << "\nMinimum Spanning Tree Edges (w/ cost)\n" << endl;
    int sum {0};
    for (int i {0}; i<V-2; i++){
        int c = G[T[0][i]][T[1][i]];
        cout << "[" << T[0][i] << "]---[" << T[1][i] << "] cost: " << c << endl;
        sum += c;
    }
    cout << endl;
    cout << "Total cost of MST: " << sum << endl;
}

void PrimsMST(int G[V][V], int n){
    int u;
    int v;
    int min {I};
    int track [V];
    int T[2][V-2] {0};

    // Initial: Find min cost edge
    for (int i {1}; i<V; i++){
        track[i] = I;  // Initialize track array with INFINITY
        for (int j {i}; j<V; j++){
            if (G[i][j] < min){
                min = G[i][j];
                u = i;
                v = j;
            }
        }
    }
    T[0][0] = u;
    T[1][0] = v;
    track[u] = track[v] = 0;

    // Initialize track array to track min cost edges
    for (int i {1}; i<V; i++){
        if (track[i] != 0){
            if (G[i][u] < G[i][v]){
                track[i] = u;
            } else {
                track[i] = v;
            }
        }
    }

    // Repeat
    for (int i {1}; i<n-1; i++){
        int k;
        min = I;
        for (int j {1}; j<V; j++){
            if (track[j] != 0 && G[j][track[j]] < min){
                k = j;
                min = G[j][track[j]];
            }
        }
        T[0][i] = k;
        T[1][i] = track[k];
        track[k] = 0;

        // Update track array to track min cost edges
        for (int j {1}; j<V; j++){
            if (track[j] != 0 && G[j][k] < G[j][track[j]]){
                track[j] = k;
            }
        }
    }
    PrintMST(T, G);
}

int main() {

    int cost [V][V] {
            {I, I, I, I, I, I, I, I},
            {I, I, 25, I, I, I, 5, I},
            {I, 25, I, 12, I, I, I, 10},
            {I, I, 12, I, 8, I, I, I},
            {I, I, I, 8, I, 16, I, 14},
            {I, I, I, I, 16, I, 20, 18},
            {I, 5, I, I, I, 20, I, I},
            {I, I, 10, I, 14, 18, I, I},
    };

    int n = sizeof(cost[0])/sizeof(cost[0][0]) - 1;

    PrimsMST(cost, n);

    return 0;
}

Kruskal’s Spanning Tree

  • Local 만 고려해서 엣지가 가장 작은 값만으로 Heap에다가 Node address 저장하는 것

DisJoint Subset Program

Kruskal’s Subset Program

  • 작은 값들 엣지를 먼저 정렬한다.

  • five should go to this 7 because this is the parent of this.
  • Edge의 최소값과, Set 그리고 Edge들의 Node를 활용 했지는 지 안했는지의 Included Hash

#include <iostream>

#define I 32767  // Infinity
#define V 7  // # of vertices in Graph
#define E 9  // # of edges in Graph

using namespace std;

void PrintMCST(int T[][V-1], int A[][E]){
    cout << "\nMinimum Cost Spanning Tree Edges\n" << endl;
    for (int i {0}; i<V-1; i++){
        cout << "[" << T[0][i] << "]-----[" << T[1][i] << "]" << endl;
    }
    cout << endl;
}

// Set operations: Union and Find
void Union(int u, int v, int s[]){
    if (s[u] < s[v]){
        s[u] += s[v];
        s[v] = u;
    } else {
        s[v] += s[u];
        s[u] = v;
    }
}

int Find(int u, int s[]){
    int x = u;
    int v = 0;

    while (s[x] > 0){
        x = s[x];
    }

    while (u != x){
        v = s[u];
        s[u] = x;
        u = v;
    }
    return x;
}

void KruskalsMCST(int A[3][9]){
    int T[2][V-1];  // Solution array
    int track[E] {0};  // Track edges that are included in solution
    int set[V+1] = {-1, -1, -1, -1, -1, -1, -1, -1};  // Array for finding cycle

    int i {0};
    while (i < V-1){
        int min = I;
        int u {0};
        int v {0};
        int k {0};

        // Find a minimum cost edge
        for (int j {0}; j<E; j++){
            if (track[j] == 0 && A[2][j] < min){
                min = A[2][j];
                u = A[0][j];
                v = A[1][j];
                k = j;
            }
        }

        // Check if the selected min cost edge (u, v) forming a cycle or not
        if (Find(u, set) != Find(v, set)){
            T[0][i] = u;
            T[1][i] = v;

            // Perform union
            Union(Find(u, set), Find(v, set), set);
            i++;
        }
        track[k] = 1;
    }

    PrintMCST(T, A);
}

int main() {
    int edges[3][9] = { 1, 1,  2,  2, 3,  4,  4,  5,  5},
                       { 2, 6,  3,  7, 4,  5,  7,  6,  7},
                       {25, 5, 12, 10, 8, 16, 14, 20, 18}; // {} 이거 더 있어야 한다.

    KruskalsMCST(edges);

    return 0;
}

Quiz

Comments