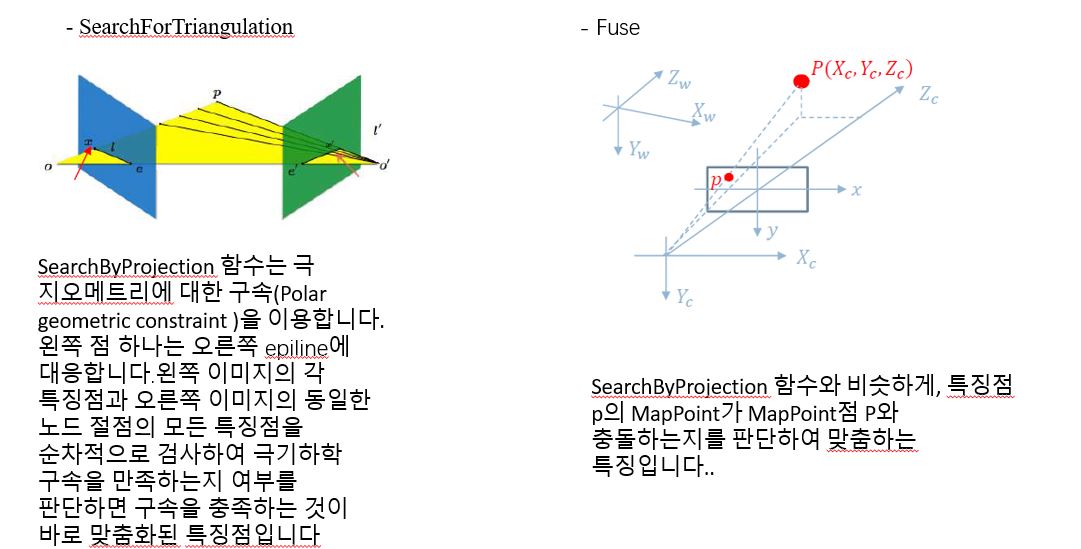
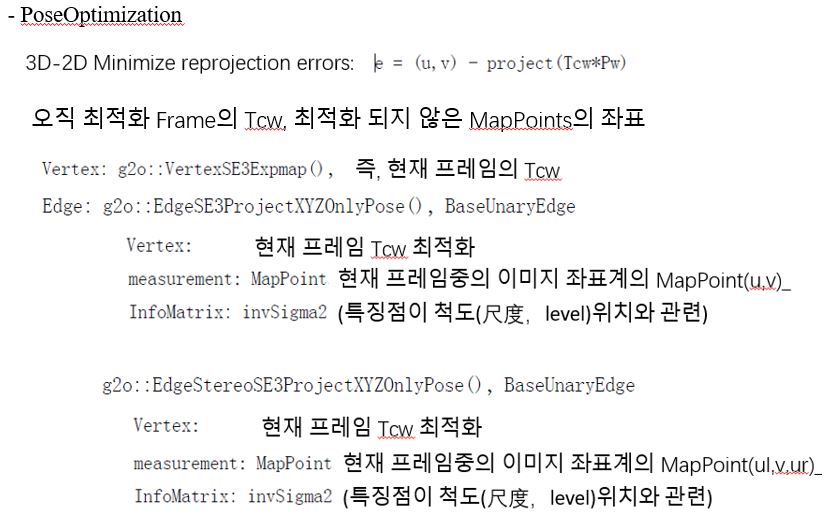
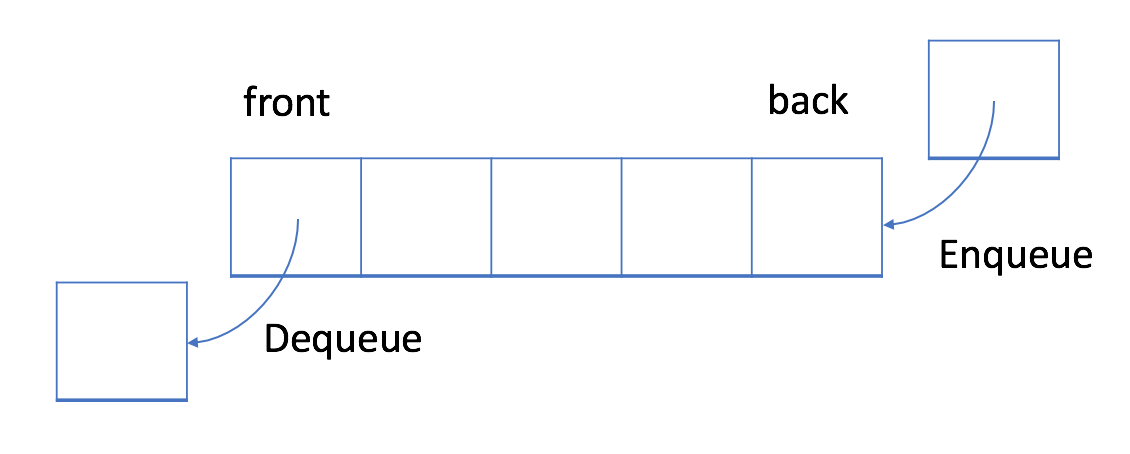
MS round2 준비
15 Apr 2020 | daily
처참하게 코딩테스트에 떨어졌다. 예견했던 일이다. 그만큼 준비도 안되있고 연습도 안해보았으니. 어찌 첫술에 배부르랴. 하지만 마이크로소프트 리크루팅 팀에서 다른 직위의 Job Offer를 주었다.
흐음 이 직책은 어찌 되었건 예전에 다닌던 회사 CS업무하고 비슷한거 같다.
MS 면접 기회를 받은것도 어디인가, 어떤 직위이건 좋은 경험이 될거 같아 면접 준비하기로 했다.
면접에는 기술면접 2번, 합격을 하면 매니저 면접이 있다.
인터넷을 조사한 결과 기술면접에 질문들은 대략
- 영어 자기소개
- 프로젝트 경험
- 이력서 기준으로 질문
이렇게 되는 거 같다. 소프트웨어 직군 같은경우 위에 질문에 추가로 Algorith 문제 푸는 질문은 한다는데 Support Engineer은 그런것이 없는 것 같다.
주로 글로벌 커스터머 상대다 보니 영어에 대한 질문이 많고, Trouble Shooting에 대한 Process와
유투브나 인터넷에서 조사한 것을 보면
극한의 상황에 대한 질문도 주어진다고 한다.
예를 들어
- 나의 할일은 꽉 차있고, 업무도 마무리 못했는데, 팀메이트들이 회의를 하자고 한다. 갈것인가 말것인가 등
곤란한 질문을 한다고 한다. 아마 단체 팀워크에 맞는지에 관한 질문들을 하는 것 같다.
처참하게 코딩테스트에 떨어졌다. 예견했던 일이다. 그만큼 준비도 안되있고 연습도 안해보았으니. 어찌 첫술에 배부르랴. 하지만 마이크로소프트 리크루팅 팀에서 다른 직위의 Job Offer를 주었다.
흐음 이 직책은 어찌 되었건 예전에 다닌던 회사 CS업무하고 비슷한거 같다. MS 면접 기회를 받은것도 어디인가, 어떤 직위이건 좋은 경험이 될거 같아 면접 준비하기로 했다.
면접에는 기술면접 2번, 합격을 하면 매니저 면접이 있다.
인터넷을 조사한 결과 기술면접에 질문들은 대략
- 영어 자기소개
- 프로젝트 경험
- 이력서 기준으로 질문
이렇게 되는 거 같다. 소프트웨어 직군 같은경우 위에 질문에 추가로 Algorith 문제 푸는 질문은 한다는데 Support Engineer은 그런것이 없는 것 같다.
주로 글로벌 커스터머 상대다 보니 영어에 대한 질문이 많고, Trouble Shooting에 대한 Process와
유투브나 인터넷에서 조사한 것을 보면 극한의 상황에 대한 질문도 주어진다고 한다. 예를 들어
- 나의 할일은 꽉 차있고, 업무도 마무리 못했는데, 팀메이트들이 회의를 하자고 한다. 갈것인가 말것인가 등
곤란한 질문을 한다고 한다. 아마 단체 팀워크에 맞는지에 관한 질문들을 하는 것 같다.