15. SMILING FACES DETECTOR
15 Sep 2019 | Python
PROBLEM STATEMENT
- The dataset contains a series of images that can be used to solve the Happy House problem!
- We need to build an artificial neural network that can detect smiling faces
- Only smiling people will be allowed to enter the house!
- The train set has 600 examples. The test set has 150 examples.
- Data Source: https://www.kaggle.com/iarunava/happy-house-dataset
Step 1 Importing data
# import libraries
import pandas as pd # Import Pandas for data manipulation using dataframes
import numpy as np # Import Numpy for data statistical analysis
import matplotlib.pyplot as plt # Import matplotlib for data visualisation
import seaborn as sns
import h5py
# read our specific image.
# the h5py is a pythonic interface to the HDF5 Binary data format
#HDF5(Hierarchical Data Format Version 5) :대용량 데이터를 저장하기 위한 파일 포맷
import random
filename = 'train_happy.h5'
f = h5py.File(filename, 'r')
#.File <- it have to be capitalized 'F'
for key in f.keys():
print(key)
#Names of the groups in HDF5 file.
# let's get key from file
# it contain simply.
list_classes
train_set_x
train_set_y
happy_training = h5py.File('train_happy.h5', "r")
happy_testing = h5py.File('test_happy.h5', "r")
X_train = np.array(happy_training["train_set_x"])
# we want to get all the data of train_set_x
y_train = np.array(happy_training["train_set_y"])
X_test = np.array(happy_testing["test_set_x"])
y_test = np.array(happy_testing["test_set_y"])
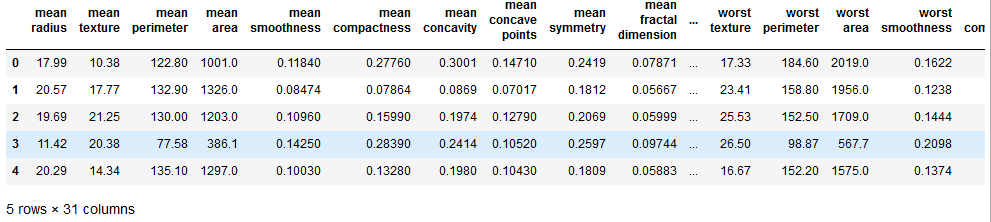
X_train.shape
# 64, 64 is the martrix
# 600 images
y_train
# 0 is no smile,
# 1 is smiling
y_train.shape
# (600,)
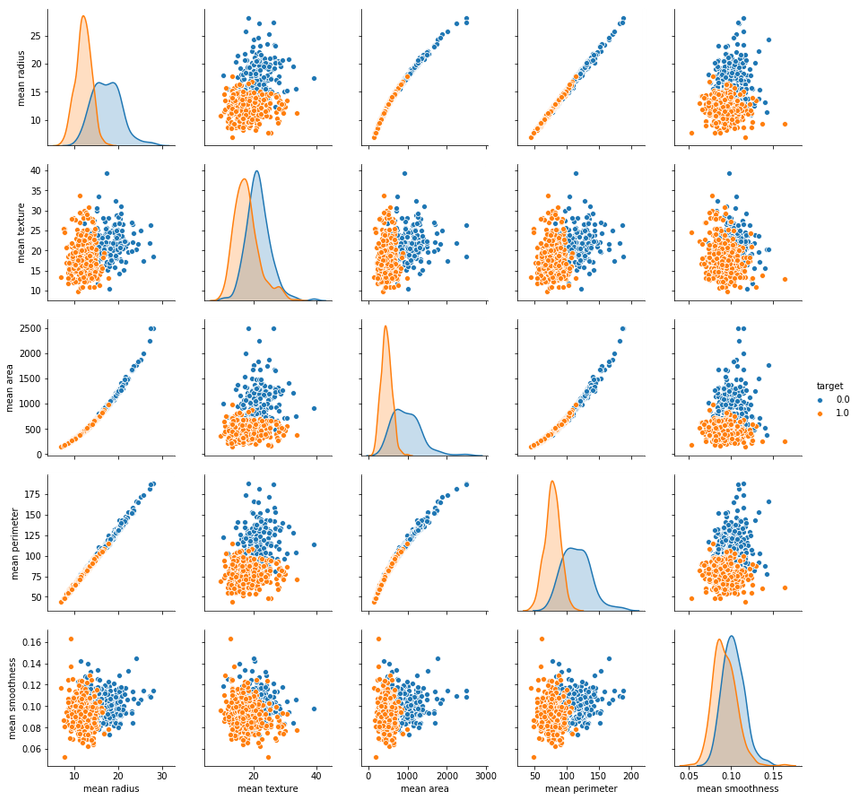
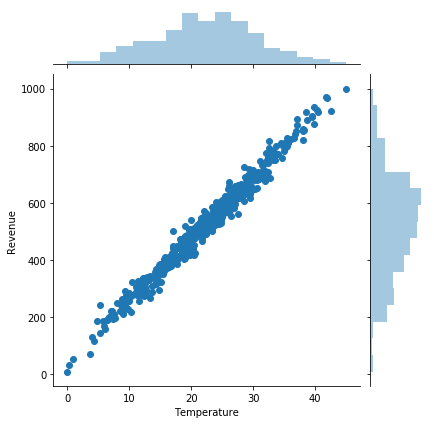
Step 2 Visualize data
i = random.randint(1,600) # select any random index from 1 to 600
plt.imshow( X_train[i] )
print(y_train[i]) # 0
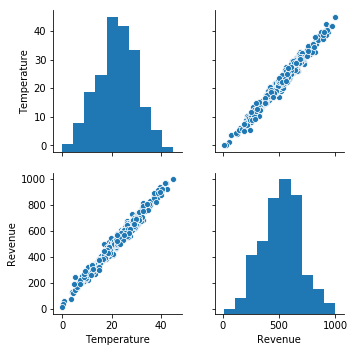
# Let's view more images in a grid format
# Define the dimensions of the plot grid
W_grid = 5
L_grid = 5
# fig, axes = plt.subplots(L_grid, W_grid)
# subplot return the figure object and axes object
# we can use the axes object to plot specific figures at various locations
fig, axes = plt.subplots(L_grid, W_grid, figsize = (25,25))
axes = axes.ravel() # flaten the 15 x 15 matrix into 225 array
# return contiguous(인접한) flattened array(1D array with all the input-array elements and with the same type)
n_training = len(X_train) # get the length of the training dataset
# Select a random number from 0 to n_training
for i in np.arange(0, W_grid * L_grid): # create evenly spaces variables
# Select a random number
index = np.random.randint(0, n_training)
# read and display an image with the selected index
axes[i].imshow( X_train[index])
axes[i].set_title(y_train[index], fontsize = 25)
#this is showing that 0,1 for reconition of smile or not
axes[i].axis('off')
#axis('off') means that remove the coordinate point
plt.subplots_adjust(hspace=0.4)
#subplots_adjust(hspace =0.4) is that adjust distance between pictures
Step 3 MODEL TRAINING
# Let's normalize dataset
X_train = X_train/255
# the picture is indicating from white color
X_test = X_test/255
X_train.shape
#(600, 64, 64, 3)
y_train.shape
# (600,)
# Import train_test_split from scikit library
# tope of tensorflow algorithm
from keras.models import Sequential
# we build neuro network by sequential fashion
from keras.layers import Conv2D, MaxPooling2D, Dense, Flatten, Dropout
# dense for full connected artificial network whichh is right hand side
from keras.optimizers import Adam
#adam optimzation
from keras.callbacks import TensorBoard
#tensorboard. actual train the model.
cnn_model = Sequential()
cnn_model.add(Conv2D(64, 6, 6, input_shape = (64,64,3), activation='relu'))
# this is convolution layer
# 64 kernal, the dimensition at each is 6 x 6
# input shape that basicaally the shape of the actual image that was feeding to our network
# relu output will be sigmoid funciton but if value is '-'(minus) it gonna be 0
cnn_model.add(MaxPooling2D(pool_size = (2, 2)))
# add max pooling layer
cnn_model.add(Dropout(0.2))
# 20percent randomly dropout
cnn_model.add(Conv2D(64, 5, 5, activation='relu'))
#this is another convolution layer
#we dont want to add input_shape, because it doesnt make sense
# here we dont have a input
# because the output coming out from the upper layer is we're going to
# be fed as an input to this layer
cnn_model.add(MaxPooling2D(pool_size = (2, 2)))
cnn_model.add(Flatten())
cnn_model.add(Dense(output_dim = 128, activation = 'relu')) #output network
#this is the hidden layer, one of the layers within our fully connected layer
cnn_model.add(Dense(output_dim = 1, activation = 'sigmoid'))
#last out in the network, our output dimension 1
#dimension 1 is because we only have one output, kind of binary output.
#the output have to be sigmoid. because after copile,
#the tensorflower have to be calculated in binary
cnn_model.compile(loss ='binary_crossentropy', optimizer=Adam(lr=0.001),metrics =['accuracy'])
#'binary_crossentropy' because our output value is the binary
#if our classifying 10 categories, we used binary_categories
#lr <= learning rate.
#we want to train metrices as accurarcy
epochs = 5
#复数,时期 : how may times we're going to be update
#update 5 times.
history = cnn_model.fit(X_train,
y_train,
batch_size = 30,
nb_epoch = epochs,
verbose = 1)
# batch_size means that how many imagees would get to be fed
# batch : 자료를 모아 두었다가 일괄해서 처리하는 자료처리의 형태
#verbose is that how many detailes we're going to be sure we actually performaing the trainig
history
Epoch 1/5
600/600 [==============================] - 9s 15ms/step - loss: 0.2444 - acc: 0.9050
Epoch 2/5
600/600 [==============================] - 9s 14ms/step - loss: 0.2150 - acc: 0.9183
Epoch 3/5
600/600 [==============================] - 9s 15ms/step - loss: 0.1829 - acc: 0.9267
Epoch 4/5
600/600 [==============================] - 9s 15ms/step - loss: 0.1931 - acc: 0.9183
Epoch 5/5
600/600 [==============================] - 9s 15ms/step - loss: 0.1662 - acc: 0.9300
Step 4 EVALUATING THE MODEL
evaluation = cnn_model.evaluate(X_test, y_test)
# evaaluating from the data set
evaluation
# [0.3277119962374369, 0.8799999968210857]
print('Test Accuracy : {:.3f}'.format(evaluation[1]))
# loacation in number one. so we have simply event contain two value zero
# numpy array
# Test Accuracy : 0.880
# get the predictions for the test data
predicted_classes = cnn_model.predict_classes(X_test)
predicted_classes.shape
#bunch of 1 or 0
# guess coming out from the guess train data
# (150, 1)
y_test.shape
# (150,)
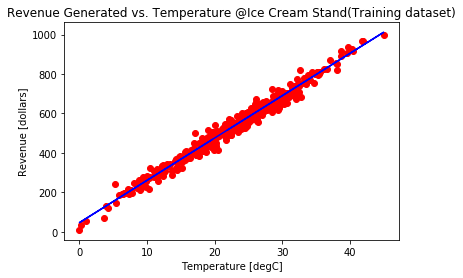
L = 5
W = 5
fig, axes = plt.subplots(L, W, figsize = (12,12))
axes = axes.ravel() #
for i in np.arange(0, L * W):
axes[i].imshow(X_test[i])
axes[i].set_title("Prediction Class = {}\n True Class = {}".format(predicted_classes[i], y_test[i]))
axes[i].axis('off')
plt.subplots_adjust(wspace=0.5)
# axes[i].set_title("Guess{}\n True{}".format(predicted_class[i], y_test[i]))
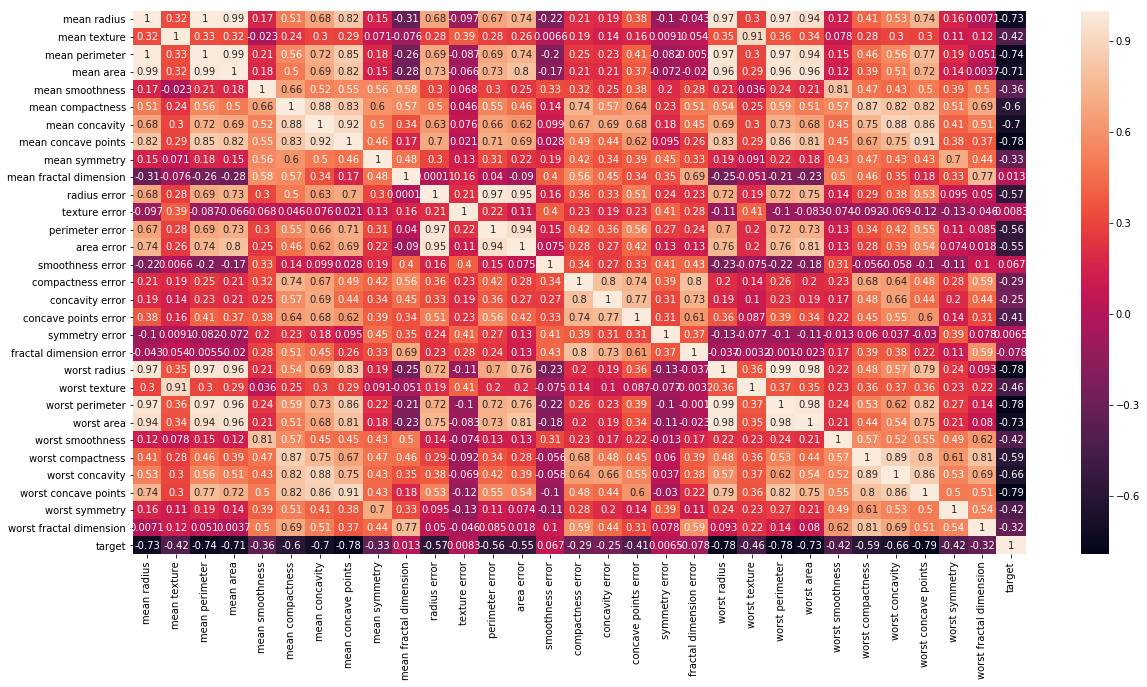
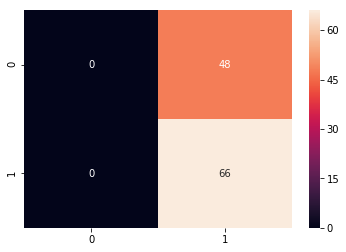
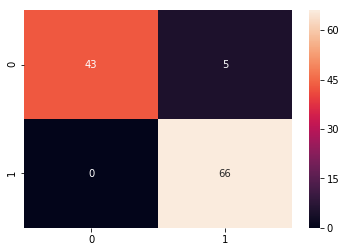
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, predicted_classes)
plt.figure(figsize = (10,10))
sns.heatmap(cm, annot=True)
# Sum the diagonal element to get the total true correct values
from sklearn.metrics import classification_report
print(classification_report(y_test.T, predicted_classes))
precision recall f1-score support
0 0.94 0.77 0.85 66
1 0.84 0.96 0.90 84
micro avg 0.88 0.88 0.88 150
macro avg 0.89 0.87 0.88 150
weighted avg 0.89 0.88 0.88 150
PROBLEM STATEMENT
- The dataset contains a series of images that can be used to solve the Happy House problem!
- We need to build an artificial neural network that can detect smiling faces
- Only smiling people will be allowed to enter the house!
- The train set has 600 examples. The test set has 150 examples.
- Data Source: https://www.kaggle.com/iarunava/happy-house-dataset
Step 1 Importing data
# import libraries
import pandas as pd # Import Pandas for data manipulation using dataframes
import numpy as np # Import Numpy for data statistical analysis
import matplotlib.pyplot as plt # Import matplotlib for data visualisation
import seaborn as sns
import h5py
# read our specific image.
# the h5py is a pythonic interface to the HDF5 Binary data format
#HDF5(Hierarchical Data Format Version 5) :대용량 데이터를 저장하기 위한 파일 포맷
import random
filename = 'train_happy.h5'
f = h5py.File(filename, 'r')
#.File <- it have to be capitalized 'F'
for key in f.keys():
print(key)
#Names of the groups in HDF5 file.
# let's get key from file
# it contain simply.
list_classes
train_set_x
train_set_y
happy_training = h5py.File('train_happy.h5', "r")
happy_testing = h5py.File('test_happy.h5', "r")
X_train = np.array(happy_training["train_set_x"])
# we want to get all the data of train_set_x
y_train = np.array(happy_training["train_set_y"])
X_test = np.array(happy_testing["test_set_x"])
y_test = np.array(happy_testing["test_set_y"])
X_train.shape
# 64, 64 is the martrix
# 600 images
y_train
# 0 is no smile,
# 1 is smiling
y_train.shape
# (600,)
Step 2 Visualize data
i = random.randint(1,600) # select any random index from 1 to 600
plt.imshow( X_train[i] )
print(y_train[i]) # 0
# Let's view more images in a grid format
# Define the dimensions of the plot grid
W_grid = 5
L_grid = 5
# fig, axes = plt.subplots(L_grid, W_grid)
# subplot return the figure object and axes object
# we can use the axes object to plot specific figures at various locations
fig, axes = plt.subplots(L_grid, W_grid, figsize = (25,25))
axes = axes.ravel() # flaten the 15 x 15 matrix into 225 array
# return contiguous(인접한) flattened array(1D array with all the input-array elements and with the same type)
n_training = len(X_train) # get the length of the training dataset
# Select a random number from 0 to n_training
for i in np.arange(0, W_grid * L_grid): # create evenly spaces variables
# Select a random number
index = np.random.randint(0, n_training)
# read and display an image with the selected index
axes[i].imshow( X_train[index])
axes[i].set_title(y_train[index], fontsize = 25)
#this is showing that 0,1 for reconition of smile or not
axes[i].axis('off')
#axis('off') means that remove the coordinate point
plt.subplots_adjust(hspace=0.4)
#subplots_adjust(hspace =0.4) is that adjust distance between pictures
Step 3 MODEL TRAINING
# Let's normalize dataset
X_train = X_train/255
# the picture is indicating from white color
X_test = X_test/255
X_train.shape
#(600, 64, 64, 3)
y_train.shape
# (600,)
# Import train_test_split from scikit library
# tope of tensorflow algorithm
from keras.models import Sequential
# we build neuro network by sequential fashion
from keras.layers import Conv2D, MaxPooling2D, Dense, Flatten, Dropout
# dense for full connected artificial network whichh is right hand side
from keras.optimizers import Adam
#adam optimzation
from keras.callbacks import TensorBoard
#tensorboard. actual train the model.
cnn_model = Sequential()
cnn_model.add(Conv2D(64, 6, 6, input_shape = (64,64,3), activation='relu'))
# this is convolution layer
# 64 kernal, the dimensition at each is 6 x 6
# input shape that basicaally the shape of the actual image that was feeding to our network
# relu output will be sigmoid funciton but if value is '-'(minus) it gonna be 0
cnn_model.add(MaxPooling2D(pool_size = (2, 2)))
# add max pooling layer
cnn_model.add(Dropout(0.2))
# 20percent randomly dropout
cnn_model.add(Conv2D(64, 5, 5, activation='relu'))
#this is another convolution layer
#we dont want to add input_shape, because it doesnt make sense
# here we dont have a input
# because the output coming out from the upper layer is we're going to
# be fed as an input to this layer
cnn_model.add(MaxPooling2D(pool_size = (2, 2)))
cnn_model.add(Flatten())
cnn_model.add(Dense(output_dim = 128, activation = 'relu')) #output network
#this is the hidden layer, one of the layers within our fully connected layer
cnn_model.add(Dense(output_dim = 1, activation = 'sigmoid'))
#last out in the network, our output dimension 1
#dimension 1 is because we only have one output, kind of binary output.
#the output have to be sigmoid. because after copile,
#the tensorflower have to be calculated in binary
cnn_model.compile(loss ='binary_crossentropy', optimizer=Adam(lr=0.001),metrics =['accuracy'])
#'binary_crossentropy' because our output value is the binary
#if our classifying 10 categories, we used binary_categories
#lr <= learning rate.
#we want to train metrices as accurarcy
epochs = 5
#复数,时期 : how may times we're going to be update
#update 5 times.
history = cnn_model.fit(X_train,
y_train,
batch_size = 30,
nb_epoch = epochs,
verbose = 1)
# batch_size means that how many imagees would get to be fed
# batch : 자료를 모아 두었다가 일괄해서 처리하는 자료처리의 형태
#verbose is that how many detailes we're going to be sure we actually performaing the trainig
history
Epoch 1/5
600/600 [==============================] - 9s 15ms/step - loss: 0.2444 - acc: 0.9050
Epoch 2/5
600/600 [==============================] - 9s 14ms/step - loss: 0.2150 - acc: 0.9183
Epoch 3/5
600/600 [==============================] - 9s 15ms/step - loss: 0.1829 - acc: 0.9267
Epoch 4/5
600/600 [==============================] - 9s 15ms/step - loss: 0.1931 - acc: 0.9183
Epoch 5/5
600/600 [==============================] - 9s 15ms/step - loss: 0.1662 - acc: 0.9300
Step 4 EVALUATING THE MODEL
evaluation = cnn_model.evaluate(X_test, y_test)
# evaaluating from the data set
evaluation
# [0.3277119962374369, 0.8799999968210857]
print('Test Accuracy : {:.3f}'.format(evaluation[1]))
# loacation in number one. so we have simply event contain two value zero
# numpy array
# Test Accuracy : 0.880
# get the predictions for the test data
predicted_classes = cnn_model.predict_classes(X_test)
predicted_classes.shape
#bunch of 1 or 0
# guess coming out from the guess train data
# (150, 1)
y_test.shape
# (150,)
L = 5
W = 5
fig, axes = plt.subplots(L, W, figsize = (12,12))
axes = axes.ravel() #
for i in np.arange(0, L * W):
axes[i].imshow(X_test[i])
axes[i].set_title("Prediction Class = {}\n True Class = {}".format(predicted_classes[i], y_test[i]))
axes[i].axis('off')
plt.subplots_adjust(wspace=0.5)
# axes[i].set_title("Guess{}\n True{}".format(predicted_class[i], y_test[i]))
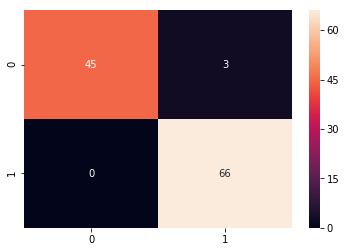
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, predicted_classes)
plt.figure(figsize = (10,10))
sns.heatmap(cm, annot=True)
# Sum the diagonal element to get the total true correct values
from sklearn.metrics import classification_report
print(classification_report(y_test.T, predicted_classes))
precision recall f1-score support
0 0.94 0.77 0.85 66
1 0.84 0.96 0.90 84
micro avg 0.88 0.88 0.88 150
macro avg 0.89 0.87 0.88 150
weighted avg 0.89 0.88 0.88 150