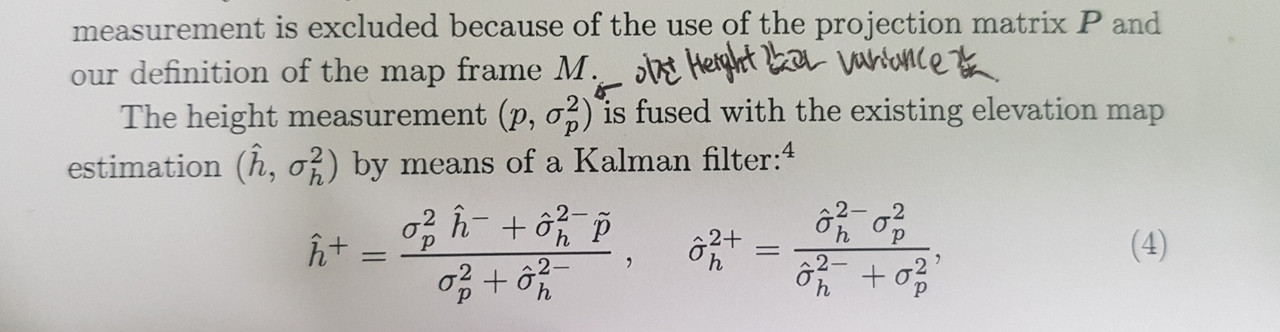Meaning of Gradient and Gradient Methods(Convex Optimization)
07 Jan 2022 | Optimization method
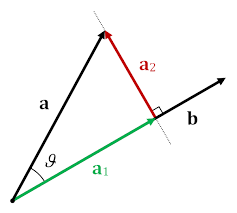
Gradient는 등산으로 따지면 현재 내 위치가 경사가 아래로 되어있는지 위로 되어있는지 보는 것이다.
우리가 등산을 할 때 가고 있는 길이 꾸불꾸불하기 때문에 우리가 가고 있는 길이 원하고 있는 목적지로 가고 있는 지는 지도가 있지 않
는 이상 경사로 확인을 할 수 가 있다.(현재 값이 결과 값과 correspoiding하지 않기 때문에)
그렇기 때문에 우리가 길을 가면서 수시로 내리막길인지 올라가는 길인지 확인을 하는 작업을 합니다(Iteration)(Global minimal 찾는 작업(목적지를 찾는 작업)
이와 마찬가지로 현실세계에서 다양한 문제가 있습니다.
ICP나 Bundle Adjustment와 같이 매칭을 통한 T,R값을 구할떄 error(측정값 - 예측값)에 대한 cost Function을 최대한 줄여서 미지수를 구하게 됩니다.
이와 같이 다양한 미지수에 대한 최적값을 찾을 떄 Gradient Decent를 많이 사용한다.
Gradient Decent가 필요한 이유는 현실 세계에서 우리는 비선형에 대한 문제를 풀게 된다.
허나 모든 데이터를 가지고 최소값을 찾는 것은 cost가 매우 큰 작업이다. 이에 다양한 방법들이 있는데 다양하게 사용하는 것은
stochastic gradient descent (SGD) : 모든 미지수를 계산하는 것이 아니라, 특정 미지수만 선택을하여서 global minimum을 찾는다.
즉, Batch set을 이용하는 방법이다.
Vanila Gradient Descent :Vanilla gradient descent means the basic gradient descent algorithm without any bells or whistles. There are many variants on gradient descent. In usual gradient descent (also known as batch gradient descent or vanilla gradient descent), the gradient is computed as the average of the gradient of each datapoint.
Vanilla algorithm meaning : In computer science, vanilla is the term used to refer when computer software and sometimes also other computing-related systems like computer hardware or algorithms are not customized from their original form, i.e., they are used without any customizations or updates applied to them.
주 최적화 방법은 즉 error function에 2차 편미분을 하여서(Jacobian Matrix, Hessian Matrix) Gaussian Newton(Decent) 방식으로 변환을 하여서, delta X에 대한 값(pose and landmark or just pose(landmark))를 x에 업데이트를 Iteration K만큼 해주면서 업데이트에 적용되는 delta x에 대해 최소값을 만드는 것이다.
다양한 방법들
https://darkpgmr.tistory.com/142?category=761008
https://darkpgmr.tistory.com/133
https://darkpgmr.tistory.com/56
https://darkpgmr.tistory.com/58
Gradient는 등산으로 따지면 현재 내 위치가 경사가 아래로 되어있는지 위로 되어있는지 보는 것이다.
우리가 등산을 할 때 가고 있는 길이 꾸불꾸불하기 때문에 우리가 가고 있는 길이 원하고 있는 목적지로 가고 있는 지는 지도가 있지 않 는 이상 경사로 확인을 할 수 가 있다.(현재 값이 결과 값과 correspoiding하지 않기 때문에)
그렇기 때문에 우리가 길을 가면서 수시로 내리막길인지 올라가는 길인지 확인을 하는 작업을 합니다(Iteration)(Global minimal 찾는 작업(목적지를 찾는 작업)
이와 마찬가지로 현실세계에서 다양한 문제가 있습니다.
ICP나 Bundle Adjustment와 같이 매칭을 통한 T,R값을 구할떄 error(측정값 - 예측값)에 대한 cost Function을 최대한 줄여서 미지수를 구하게 됩니다.
이와 같이 다양한 미지수에 대한 최적값을 찾을 떄 Gradient Decent를 많이 사용한다.
Gradient Decent가 필요한 이유는 현실 세계에서 우리는 비선형에 대한 문제를 풀게 된다.
허나 모든 데이터를 가지고 최소값을 찾는 것은 cost가 매우 큰 작업이다. 이에 다양한 방법들이 있는데 다양하게 사용하는 것은
stochastic gradient descent (SGD) : 모든 미지수를 계산하는 것이 아니라, 특정 미지수만 선택을하여서 global minimum을 찾는다.
즉, Batch set을 이용하는 방법이다.
Vanila Gradient Descent :Vanilla gradient descent means the basic gradient descent algorithm without any bells or whistles. There are many variants on gradient descent. In usual gradient descent (also known as batch gradient descent or vanilla gradient descent), the gradient is computed as the average of the gradient of each datapoint.
Vanilla algorithm meaning : In computer science, vanilla is the term used to refer when computer software and sometimes also other computing-related systems like computer hardware or algorithms are not customized from their original form, i.e., they are used without any customizations or updates applied to them.
주 최적화 방법은 즉 error function에 2차 편미분을 하여서(Jacobian Matrix, Hessian Matrix) Gaussian Newton(Decent) 방식으로 변환을 하여서, delta X에 대한 값(pose and landmark or just pose(landmark))를 x에 업데이트를 Iteration K만큼 해주면서 업데이트에 적용되는 delta x에 대해 최소값을 만드는 것이다.
다양한 방법들
https://darkpgmr.tistory.com/142?category=761008
https://darkpgmr.tistory.com/133
https://darkpgmr.tistory.com/56
https://darkpgmr.tistory.com/58