우리가 2D, 3D로 데이터가 선형적으로 분포가 되어 있다면 이에 대한 추세를 (gradient, plane model)을 구하고 싶다.

2D 같은 경우 2D line formular를 통해서 구할 수 있고,

3D 같은 경우는 3D line formular를 통해서 구할 수 있다.

이를 통해 데이터 중 outlier를 제거할 수 있고(formular로 만들어진 model에 로우 데이터를 넣어 distance 차이를 통해), 데이터의 특징을 알 수 있다.

2D Line Formular

https://www.mathcentre.ac.uk/resources/uploaded/mc-ty-strtlines-2009-1.pdf

3D Plane Fomular

https://brilliant.org/wiki/3d-coordinate-geometry-equation-of-a-plane/

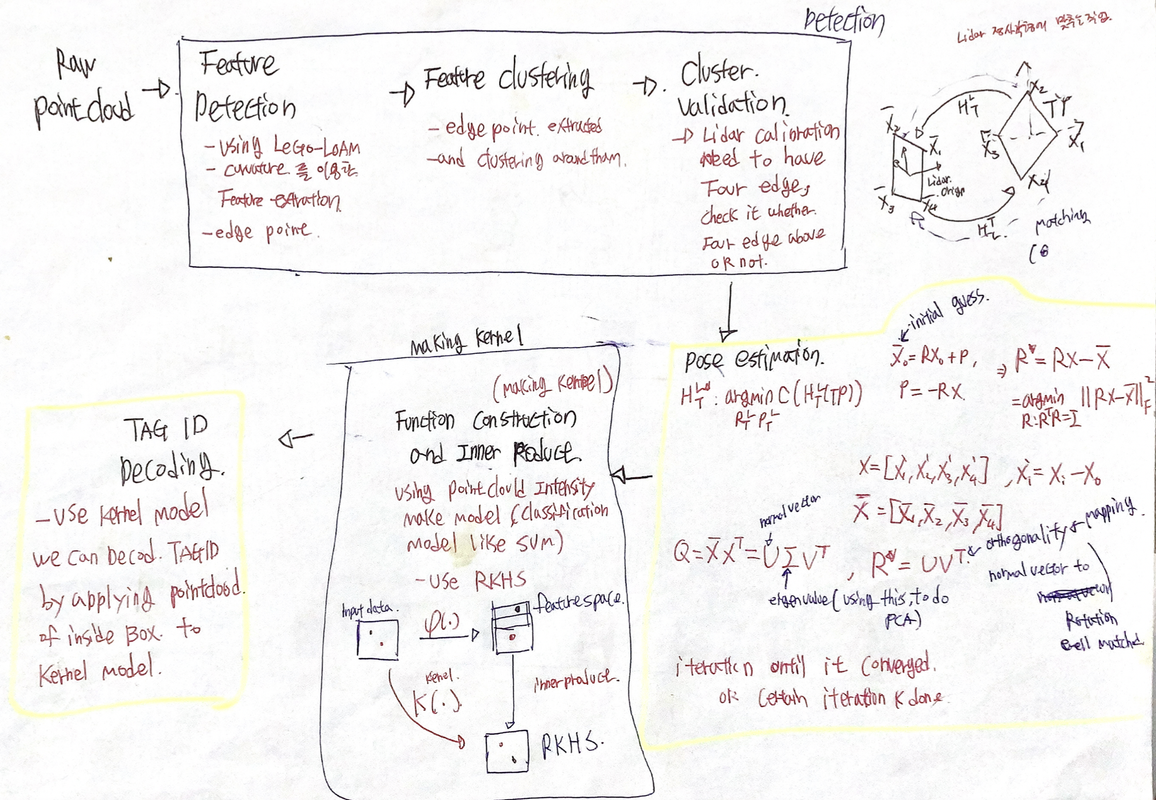
Hilbert space

힐베르트 스페이스는 거시세계 <-> 미시세계를 연결하는 역할을 한다.(Completeness)

여러 벡터(다차원의 데이터를) + - 로 계산하다 보면, 벡터 공간의 크기가 점점 커지기 때문에 문제가 될 수 있다.

이런 무한대로 커지는 벡터에 대한 크기를 방지하기 위해서 완비성(completeness)를 가진 hilbert space를 통해,

Function 과 Function간의 inner product를 통한 무한대의 벡터에 대해 수렴으로 관계를 정의할 수 있다.

이는 이후 feature map의 inner product를 통한 데이터들의 상관 관계 decision plane을 만들 수 있다.

+)f,g 여기에 함수는 PFD처럼 여러 벡터들을 함수에 넣어서 벡터마다의 output을 뽑아내고 inner product을 통해 벡터간에 similarity를 구할 수 있다.

classification에서 많이 쓰인다.

Hilbert Space 참고

https://medium.com/@brcsomnath/hilbert-space-7a36e3badac2

https://ko.wikipedia.org/wiki/%EC%8B%A4%EC%88%98%EC%9D%98_%EC%99%84%EB%B9%84%EC%84%B1

https://ko.wikipedia.org/wiki/%EC%99%84%EB%B9%84%EA%B1%B0%EB%A6%AC%EA%B3%B5%EA%B0%84

Reproducing Kernal Hilbert space

줄인말로 RKHS 라고 하는데, 즉 우리는 2D or 3D 공간상에 labeling이 되어있는 데이터들간의 구분을 위해 hyperplane을 만들고 싶은데 아무래도 non linear하고 분배가 되어 있다보니, 이 문제를 해결하고나 RKHP를 통해 Kernal(Kernal trick)을 재생성하면서 Classification에 대한 문제를 풀 수 있다.(Kernal Methods라고 하며 Machine Learning에서 많이 쓰인다. 대표적으로 SVD)

hey translate data into a higher (often infinite) dimensional space, where it is far easier to separate data points than in their native space.

Statistical Methods – RKHS are used to perform approximations of difficult statistical calculations such as Independence, Conditional Independence, and Conditional Probability.

These are the applications that drew me to learn about them. The RKHS algorithms were always the most accurate, and had much better scaling properties with increasing data size and problem dimensionality.

The kernel of the RKHS determines what types of function are available in the space, as well as the meaning of the function’s result. Different kernels produce different types of functions, but some kernels are universal, meaning that they can emulate any continuous function to within isometric isomorphism, which is a fancy way of saying “exactly the same on the outside, though it may be different inside”.

Ket of RKHS is In any real-world scenario, we will quickly run out of data when we need to condition on many variables. RKHS solves this problem by returning a continuous function that represents the distribution, meaning that we effectively have an infinite number of data points to work with.

Implementing RKHS is embarrassingly easy. It may take hundreds of pages of math to describe RKHS, but only a few lines of code to make it work.

The code sample at the bottom implements a flexible, optimized RKHS in under 30 lines of Python code. A hard coded RKHS could probably be done in 10 lines. It bothers me that it took several weeks of intense study to understand an algorithm that took me an hour to implement.

discussed the kernel above, but not any function can be a kernel. The kernel requires some basic characteristics in order to be valid. It is a function that takes one or two values, and serves two distinct purposes:

When presented two arguments, it returns a distance in Hilbert Space between the two arguments, and when presented a single argument, it translates that argument into the Hilbert Space.

It is computed by taking an inner product of its parameter with the data provided to the RKHS.

My final topic in this primer is a very important feature of RKHS, and that is linearity of operations. The RKHS behaves in many ways like normal Euclidean space. This means that if we apply linear methods in RKHS, they change their meaning in a very important way.

A linear regression in RKHS is equivalent to a non-linear regression in a complex infinite dimensional space. So points that can’t be separated by a line (or hyperplane) in their native space can be easily separated by a linear regression in RKSH.

Similarly, if we compute function of variables in Euclidean space, such as Correlation(A,B), it tells us if the variables are linearly related. A Correlation of 0 indicates that the variables are linearly independent.

If I do the same calculation in RKHS, it tells me if the variables are Independent (i.e. non-linearly uncorrelated). The same is true with nearly any linear operation – in RKHS it becomes a non-linear operation. This is exemplified by the use of “kernel methods” in machine learning, though there are many other similar uses.

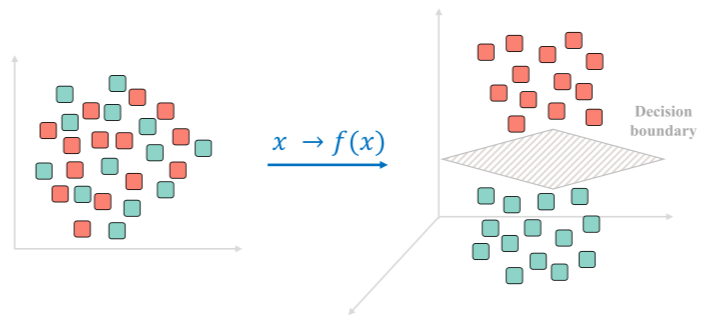
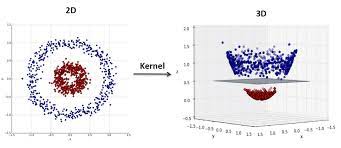
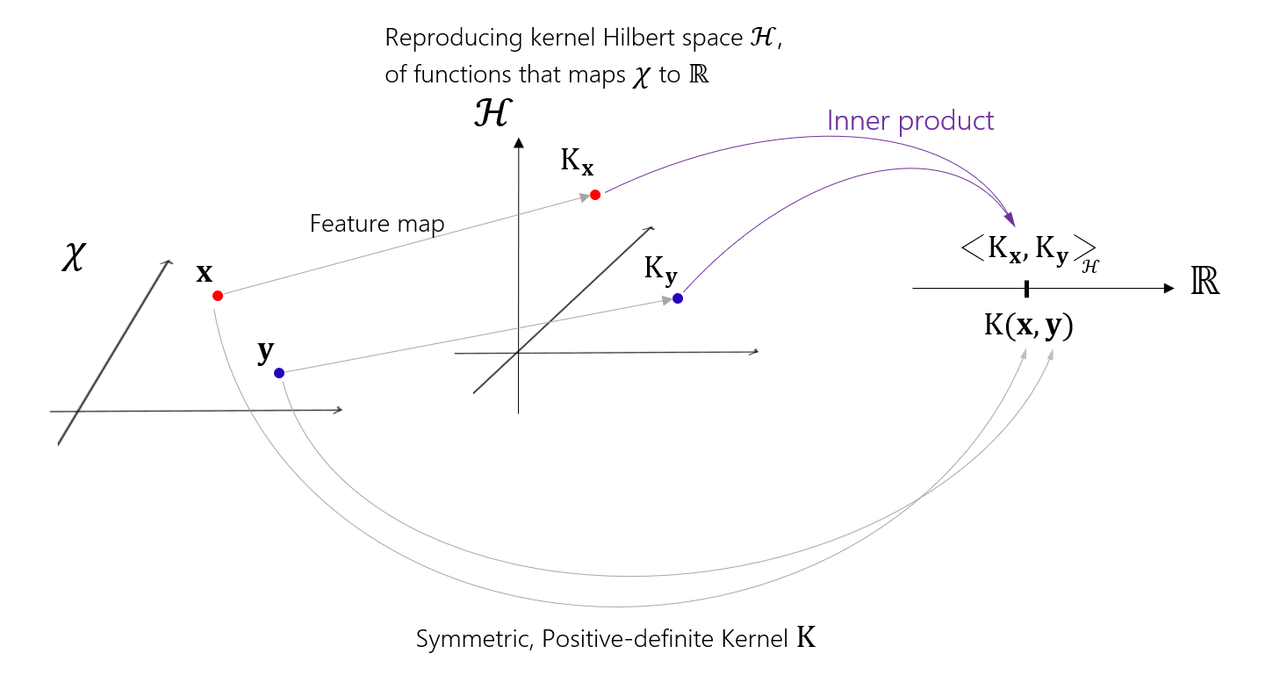
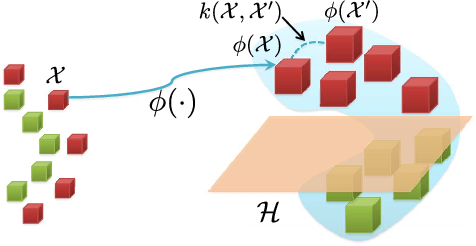
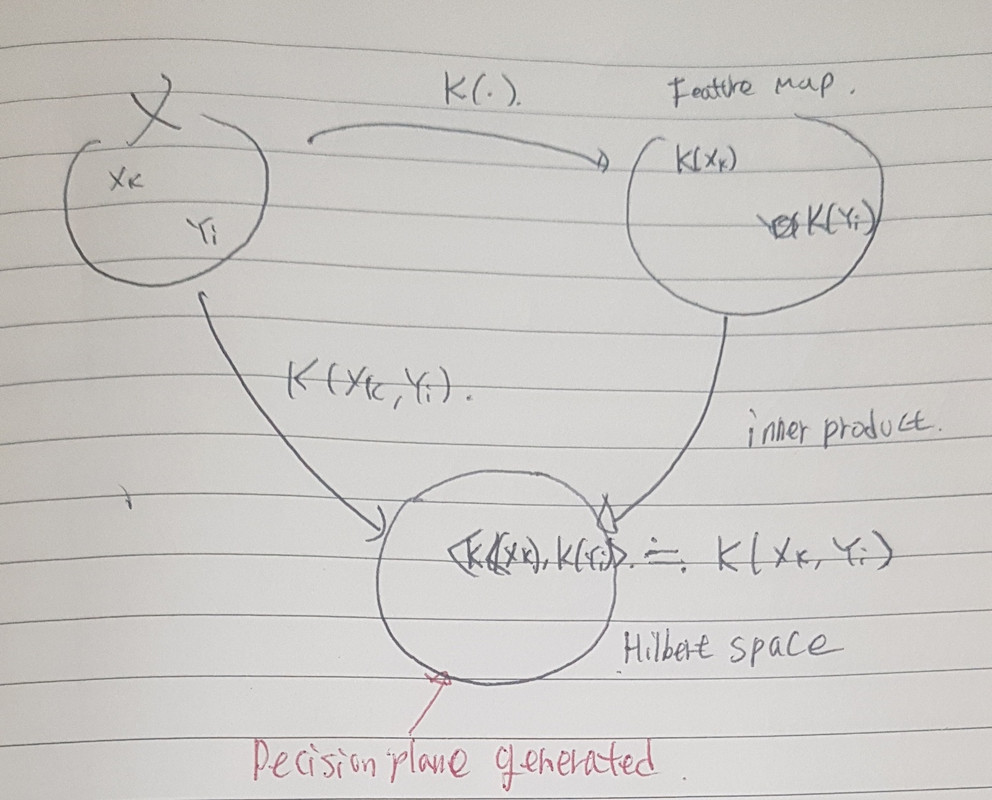
즉, feature map으로 만드는데 사용되는 function이 keneral(kernal = 특정 function, ex, PDF)이고 이를 통해서 무수히 많은 벡터들로 부터 kernal을 통한 output을 가지고, inner product을 통해 데이터간의 유사성을 판별할 수 있으며(0(orthgonal non related),1(related)), 구분할 수 있는 hyperplane(Decision plane)을 구할 수 있다. 이를 통해 kernal을 reproducing을 하여서 inner product의 값과 kenral output의 값을 같게 한다. 이를 통한 kernal을 통해 classification을 할 수 있다.

+) 만들어진 Decision plane에 데이터를 넣어서 쓰레쉬홀드를 활용한 데이터를 구분할 수 있는 모델을 만들 수도 있다.

+) 즉 inner product은 데이터간의 유사도를 확인할 때 많이 쓴다.

+) 또한 kernal을 통하여 데이터를 얻어지는데, 이를 classification으로 활용된다.

+) RKHS를 통해 다양한 데이터로 가공 할 수 있다. 예를 들어 PDF를 만든다고 할 때, 특정 데이터를 가지고 있는 벡터들과 upper, lower boundary를 가지고 있는 데이터들의 연속된 값을 Kernal을 통해 특정 데이터를 가지고 있는 벡터에 대한 PDF의 데이터 값을 만들 수있다.

+) feature map에서 inner product된 값과 kernal로 부터 아웃풋 나온 값이 같아야 한다.

엄청 설명 잘되어 있는 블로그!!

https://hpccsystems.com/blog/reproducing-RKHS

Applications

Signal Detection – RKHS are agile at separating signal from noise in communication settings.

Function Emulation – RKHS can perform the hat trick of converting a discrete set of measurements into a continuous function. This can be used, for example, to determine a Probability Density Function or a Cumulative Density Function associated with any sized data set.

Future Applications – RKHS are very flexible, and many other applications will surely be discovered.

Rproducing kernal Hilbert space 참고

https://en.wikipedia.org/wiki/Reproducing_kernel_Hilbert_space

http://songcy.net/posts/story-of-basis-and-kernel-part-1/

Fiducial Marker나 객체에 대한 pose를 찾는 방법 중 하나이다.

one is given two matrices A {\displaystyle A} A and B {\displaystyle B} B and asked to find an orthogonal matrix Ω {\displaystyle \Omega } \Omega which most closely maps A {\displaystyle A} A to B {\displaystyle B} B. [2]

즉, A와 B를 매핑하는 Orthgonal matrix(Rotation Matrix)를 찾는 법인데, 두 매트릭스에서의 엘레멘트 평균값 - 매트릭스 에 대해 dot product을 해서 H 행렬을 만들고, SVD를 통해 Rotation matrix를 구한다.

최소 4개의 점을 가지고 있는 것이 좋다.

# Integral 코드에서 쓰이는 Procrustes analysis
def rigid_transform_3D(A, B):
	centroid_A = np.mean(A, axis = 0) // all point mean value of x y z
	centroid_B = np.mean(B, axis = 0) // all point mean value of x y z
 	H = np.dot(np.transpose(A - centroid_A), B - centroid_B)  // all points of raw x y z value - mean value, dot product A,B number of points become 3x3
 	U, s, V = np.linalg.svd(H)
 	R = np.dot(np.transpose(V), np.transpose(U))
  # 만약 Rotation Matrix에 대한 Determinant가 -이면
  # 우리가 바라보고 있는 공간상에서의 flip이 되어 있는 상태이므로
  # z축을 기반으로 -를 해주면 flip이 되서 우리가 바라보고 있는 공간상의 rotation matrix를 얻게 된다.
 	if np.linalg.det(R) < 0:
 		V[2] = -V[2]
 		R = np.dot(np.transpose(V), np.transpose(U))
 	t = -np.dot(R, np.transpose(centroid_A)) + np.transpose(centroid_B)
 	return R, t
def rigid_align(A, B):
	R, t = rigid_transform_3D(A, B)
	A2 = np.transpose(np.dot(R, np.transpose(A))) + t
	return A2

이것에 대한 설명 개굿

https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/04/06/pcasvdlsa/

https://math.stackexchange.com/questions/947867/how-to-prove-invariance-of-dot-product-to-rotation-of-coordinate-system

https://redstarhong.tistory.com/55 [

https://redstarhong.tistory.com/55

https://mathworld.wolfram.com/FrobeniusNorm.html

https://simonensemble.github.io/2018-10/orthogonal-procrustes.html

https://en.wikipedia.org/wiki/Orthogonal_Procrustes_problem

Main Concept

正态分布变换算法是一个配准算法，他应用于三维点的统计模型，使用标准最优化技术来确定联合和点云间的最优的匹配，因为其在配准过程中不利用对应点的特征计算和匹配，所以时间比其他方法快。即类似与图像匹配一样的三维点云匹配。

NDT算法使用牛顿法进行参数优化

当使用NDT配准时，目标是找到当前扫描的姿态

STEP

1. 将空间（reference scan）划分成各个格子cell

2.将点云投票到各个格子

3.计算格子的正态分布PDF参数

4.将第二幅scan的每个点按转移矩阵T的变换

5.第二幅scan的点落于reference的哪个 格子，计算响应的概率分布函数

6.求所有点的最优值，目标函数为

즉, 그리드 셀을 정하고, epsilon, stepsize를 정한다.

// Setting scale dependent NDT parameters
// Setting minimum transformation difference for termination condition.
ndt.setTransformationEpsilon (0.01);
// Setting maximum step size for More-Thuente line search.
ndt.setStepSize (0.1);
//Setting Resolution of NDT grid structure (VoxelGridCovariance).
ndt.setResolution (1.0);

// how many update
ndt.setMaximumIterations (35);

그 다음 first scan 데이터를 가지고 셀에 포함된 포인트들의 mean(q) 과 covariance matrix를 만든다.

+) 초기 intial transformation matrix값은 odometry 값이나 zero로 한다.

만든 이후, second scan 데이터(x)를 지정한 셀에 투입을 하여서 PDF를 구하는데, 우리는 이에 대한 PDF 합을 score처리를 할 것이다. “score(p)=sum of exp((-(x-q)^t * Covariance matrix * (x-q))/2)”

여기서 p는 vector of parameters = (tx, ty, theta) 이다.

우리의 목적은 이제 score를 높임(optimal parameter)를 얻음으로써 모든 포인트를 업데이트를 해주고 R, T를 구하는 것이다.

이에 사용하는 방법은 최적화 알고리즘인 Newton algorithm을 사용한다.

//Newton algorithm
H * delta_p = -g;

// updating parameter p.
p <- p + delta_p

Newton Algorithm으로 p파라미터를 최적화를 할때, 위에 set한 stepsize와 epsilon을 이용하여서 iterations 수 만큼, Converge 될때까지 한다.

얻어진 p의 데이터 값은, R,t 값으로 second scan 데이터를 업데이트 시켜주고, 로봇의 포즈를 얻는다.

이 작업을 반복적으로 한다. incrementaly 하게 반복적으로 한다.

3D

https://blog.csdn.net/qq_40216084/article/details/107618766

https://zhuanlan.zhihu.com/p/94993060

2D

https://www.cnblogs.com/chenlinchong/p/12023978.html

综合

https://www.cnblogs.com/yhlx125/p/5749770.html

CODE

https://gitee.com/xiaojake/xchu_slam/tree/master/xchu_slam

https://github.com/search?q=ndt+slam

https://github.com/XiaoJake/xchu_slam/blob/master/xchu_slam/src/xchu_slam.cpp

Decode를 할때에는 Pointcloud Intensity에 따라 흑인지 백인지 구분을 하여서 bit형식 및 크기를 통해서 ID를 추출해 낸다.