27. Computational Complexity(작업 처리 속도)
27 Sep 2019 | C++
복잡도(complexity)
- 컴퓨터 공학에서 계산속도가 빠르다라는 말은 주관적일 수 밖에 없습니다.
- 따라서 어떠한 작업의 수행 속도를 나타내기 위해선 수학적으로 나타내야 합니다.
- 컴퓨터 공학에선 어떠한 작업의 처리 속도를 복잡도(complexity) 라고 부르고, 그 복잡도를 Big O 표기법이라는 것으로 나타냅니다.
- 이 표기법은, NN 개의 데이터가 주어져 있을 때 그 작업을 수행하기 위해 몇 번의 작업을 필요로 하는지 NN 에 대한 식으로 표현하는 방식입니다.
- 복잡도가 클수록 작업 수행하는데 걸리는 시간이 늘어난다.
- 예제 버블 정렬의 코드와 함께 복잡도를 보겠습니다.
for (int i = 0; i < N; i++) {
for (int j = i + 1; j < N; j++) {
if (arr[i] > arr[j]) {
swap(arr, i, j)
}
}
}
- N 개의 원소가 있는 arr 이라는 배열을 정렬하기 위해서는 일단 적어도:
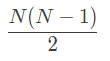
- 번의 반복이 필요 합니다. ((N-1+N-2+…+1)) 따라서 Big O 표현법으로 이 정렬이 얼마나 빠르게 수행될 수 있는지 나타낸다면 :
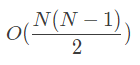
- 보통 Big O 표현법으로 나타낼 때 최고 차항만을 나타냅니다.(그리고 통상적으로 최고 차항의 계수도 생략합니다.). 왜냐하면 N 이 엄청 커지게 되면 최고 차항 말고는 그닥 의미가 없기 때문입니다.
- 따라서 버블 정렬 알고리즘의 복잡도는 : O($N^2$)
- 일반적으로 알고리즘이 O($N^2$) 꼴이면 좋은 편은 아닙니다. 왜냐하면 N 이 10000만 되더라도 $10^8$번의 작업처리를 해야하기 떄문입니다.
- 다행이도 정렬 알고리즘의 경우 퀵소트(Quicksort)라는 알고리즘을 활용하면 아래와 같은 복잡도로 연산을 처리할 수 있습니다.
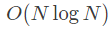
- 물론 퀵소트 알고리즘을 사용했을 때 항상 버블 정렬 방식 보다 빠르게 정렬할 수 있다는 의미는 아닙니다.
- 왜냐하면 저 항 앞에 어떠한 계수가 붙어있는지 알 수 없기 때문이지요. 만약에 버블 정렬이 O($N^2$)이고 퀵소트가 O(100000NlogN)이였다면 N이 1000일 떄 버블 정렬이 더 빠르게 수행 됩니다.(물론 이렇게 극단적이지 않습니다. 퀵소트가 거의 대부분 더 빠르게 됩니다)
- 하지만, NN 이 정말 커진다면 언젠가는 퀵소트가 버블 정렬보다 더 빨리 수행되는 때가 발생합니다.
- 아래와 차트를 보면 각각의 O에 대해 복잡도가 어떻게 증가하는지 볼 수 있습니다.
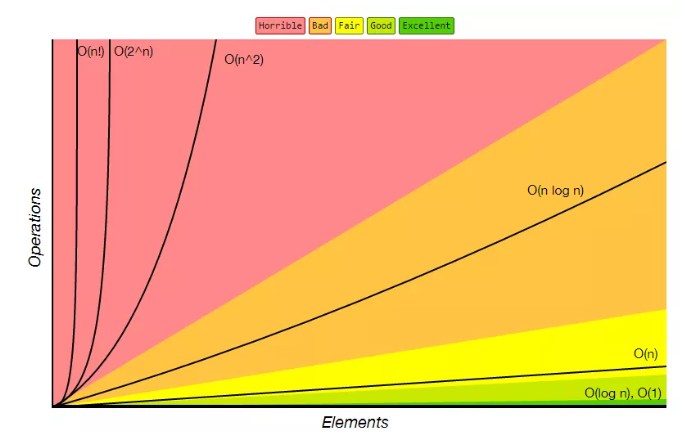
- 가장 이상적인 복잡도는 O(1)O(1) 이지만 이는 거의 불가능하고 (이는 마치 전체 데이터를 채 보지 않은 채 작업을 끝낼 수 있다는 의미 입니다), 보통 O(logn)O(logn) 이 알고리즘이 낼 수 있는 가장 빠른 속도를 의미합니다. 그 다음으로 좋은 것이 당연히 O(n)O(n) 이고, O(nlogn)O(nlogn) 순 입니다.
REFERENCE
복잡도(complexity)
- 컴퓨터 공학에서 계산속도가 빠르다라는 말은 주관적일 수 밖에 없습니다.
- 따라서 어떠한 작업의 수행 속도를 나타내기 위해선 수학적으로 나타내야 합니다.
- 컴퓨터 공학에선 어떠한 작업의 처리 속도를 복잡도(complexity) 라고 부르고, 그 복잡도를 Big O 표기법이라는 것으로 나타냅니다.
- 이 표기법은, NN 개의 데이터가 주어져 있을 때 그 작업을 수행하기 위해 몇 번의 작업을 필요로 하는지 NN 에 대한 식으로 표현하는 방식입니다.
- 복잡도가 클수록 작업 수행하는데 걸리는 시간이 늘어난다.
- 예제 버블 정렬의 코드와 함께 복잡도를 보겠습니다.
for (int i = 0; i < N; i++) {
for (int j = i + 1; j < N; j++) {
if (arr[i] > arr[j]) {
swap(arr, i, j)
}
}
}
- N 개의 원소가 있는 arr 이라는 배열을 정렬하기 위해서는 일단 적어도:
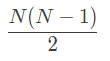
- 번의 반복이 필요 합니다. ((N-1+N-2+…+1)) 따라서 Big O 표현법으로 이 정렬이 얼마나 빠르게 수행될 수 있는지 나타낸다면 :
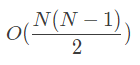
- 보통 Big O 표현법으로 나타낼 때 최고 차항만을 나타냅니다.(그리고 통상적으로 최고 차항의 계수도 생략합니다.). 왜냐하면 N 이 엄청 커지게 되면 최고 차항 말고는 그닥 의미가 없기 때문입니다.
- 따라서 버블 정렬 알고리즘의 복잡도는 : O($N^2$)
- 일반적으로 알고리즘이 O($N^2$) 꼴이면 좋은 편은 아닙니다. 왜냐하면 N 이 10000만 되더라도 $10^8$번의 작업처리를 해야하기 떄문입니다.
- 다행이도 정렬 알고리즘의 경우 퀵소트(Quicksort)라는 알고리즘을 활용하면 아래와 같은 복잡도로 연산을 처리할 수 있습니다.
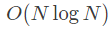
- 물론 퀵소트 알고리즘을 사용했을 때 항상 버블 정렬 방식 보다 빠르게 정렬할 수 있다는 의미는 아닙니다.
- 왜냐하면 저 항 앞에 어떠한 계수가 붙어있는지 알 수 없기 때문이지요. 만약에 버블 정렬이 O($N^2$)이고 퀵소트가 O(100000NlogN)이였다면 N이 1000일 떄 버블 정렬이 더 빠르게 수행 됩니다.(물론 이렇게 극단적이지 않습니다. 퀵소트가 거의 대부분 더 빠르게 됩니다)
- 하지만, NN 이 정말 커진다면 언젠가는 퀵소트가 버블 정렬보다 더 빨리 수행되는 때가 발생합니다.
- 아래와 차트를 보면 각각의 O에 대해 복잡도가 어떻게 증가하는지 볼 수 있습니다.

- 가장 이상적인 복잡도는 O(1)O(1) 이지만 이는 거의 불가능하고 (이는 마치 전체 데이터를 채 보지 않은 채 작업을 끝낼 수 있다는 의미 입니다), 보통 O(logn)O(logn) 이 알고리즘이 낼 수 있는 가장 빠른 속도를 의미합니다. 그 다음으로 좋은 것이 당연히 O(n)O(n) 이고, O(nlogn)O(nlogn) 순 입니다.
REFERENCE

Comments