likelihood(가능도) VS Probability(확률)
16 Mar 2021 | calculus
https://swjman.tistory.com/104
로봇공학을 공부하다 보면, 무조건 만나게 되는 개념 중에 가능도(likelihood)과 확률(Probability)라는 개념이 있다. (특히 Probabilisitic Robotics라는 엄청난 책도 있다.). 한 참 공부하다가 보면 이 기능도와 확률에 대해 헷갈리게 된다. 그래서 한번 복습할 겸 다시 한번 정리 해보고자 한다.
위키의 정의를 보면,
먼저 빈도학파의 관점에서 이야기 하며, 가능도 함수는 단순히 가능도라고 부를 수도 있고, 이것은 통계적인 모델의 파라미터의 함수를 말하는데 주어진 특정한 관찰된 데이터를 기반으로 한다. 가능도 함수들은 빈도 학파의 추론에서 주요한 역할을 하고 특히 통계치 집합으로부터 파라미터를 추정하는 방법으로 중요하다. 비공식적으로 “가능도”라는 것은 종종 “확률(Probability)”와 유사한 의미로 쓴다. 하지만 로봇공학에서는 이 두 가지 용어는 다른 의미를 지닌다.
확률이라고 하면, 주어진 모델 파라마티 값과 어떠한 관찰된 데이터에 대한 참조 없이, 랜덤 출력에 대한 일어날 뻔한 가능성이다.
즉, 로봇공학으로 이해하자면 x,y,z에 대한 관찰 데이터 값이 존재하지 않고, scale parameter도 존재하지 않지만 transition matrix 및 matrix relevant control input에 대한 모델을 통해 (x,y,z)의 변수 랜덤 출력 데이터 값을 가지고 상태에 대한 예측하는 것이다.
반면, 가능도라는 것은 주어진 특정한 관찰된 데이터를 기반으로 하여 모델 파라미터 값들이 될 뻔한 가능성이다.
즉 로봇공학으로 이해하자면 x,y,z 에 대한 관찰 값이 주어지고 이를 통해 scale parameter 및 모델 안에 존재하는 파라미터 값들을 예측하는 것이다.
그렇기 때문에 가능도와 확률의 차이는 명백하다. 위의 정의를 읽어 보면 알겠지만, 아예 대상 자체가 다르다. 확률의 경우에는 출력의 확률이다. 즉, x와 같은 랜덤 변수가 미지수가 될 것이다. 해당 랜덤 변수 x가 될 확률이 확률이고, 여기서 파라미터 값들은 다 주어진다고 본다. 그래서 연속 변수의 경우 아래와 같이 확률 밀도 함수가 확률에 대한 함수가 될 수 있겠다.
f(x|Θ)
그러면 가능도는 어떤가? 가능도의 경우에는 L이라고 따로 표기하며, 조건부의 순서가 확률과 반대인 것을 알 수 있다. 이번에는 x라는 랜덤 변수가 주어졌을 때, 세타 즉, 파라미터의 확률이 된다. 랜덤 변수가 주어진다는 것은 사실 전체 모집단에 대한 랜덤 변수를 모두 안다는 것은 불가능 하다. 그래서 위에 정의에서도 말했듯이, x는 일반적인 랜덤 변수가 아닌, 측정하거나, 알고 있는 샘플들에 해당한다. 이렇게 샘플이 있을 때, 해당 샘플이 있을 때, 파라미터들이 될 수 있는 확률이 가능도이다.
L(Θ|x)
이게 표기법 때문에 헷갈릴 수 있는데, 왜냐하면 가끔 이 둘이 수학적으로 같다고 하기 때문이다. 그런데 그것은 하나의 샘플 데이터에 대해서 이야기 한다면 같을 수 있겠지만, 보통은 하나의 샘플이 아닌 여러 개의 샘플 즉, n개의 샘플 데이터가 있는 상태에서 통계적 분석을 하게 된다. 따라서, 아래와 같은 형태가 제대로된 가능도의 형태가 된다.
무엇을 의미하는지를 잘 살펴보면, x가 의미하는 것은 여러 개의 샘플들이 되고, 각각의 샘플이 주어졌을때의 가능도를 모두 곱하게 된다. 앞에서 말했듯이, 샘플 하나에 대한 가능도는 확률과 같기 때문에(위의경우 연속 변수이니 확률 밀도 함수와 같다) 그래서 f라고 표기한 확률을 사용해서 가능도를 만들며, 앞에 곱하기 표시를 해서 각 샘플에 대해서 모두 곱하는 것이다. 여기서 왜 곱하기를 하는지 생각해보자. 그것은 다름 아닌, 아래와 같이 가능도가 샘플이 여러 개일 때, joint probability와 같게 되는데, 이 때, 각각의 샘플들의 확률들에 대해서 조인트로 일어날 확률이 가능도가 된다. 그런데 보통 샘플들을 취급할때, 독립성을 가정하기 때문에 조인트 확률은 단지 곱셈으로 대체가 되기 때문에 이러한 곱셈이 적용될 수 있다는 것도 기억하자.
EXAMPLES
Probability
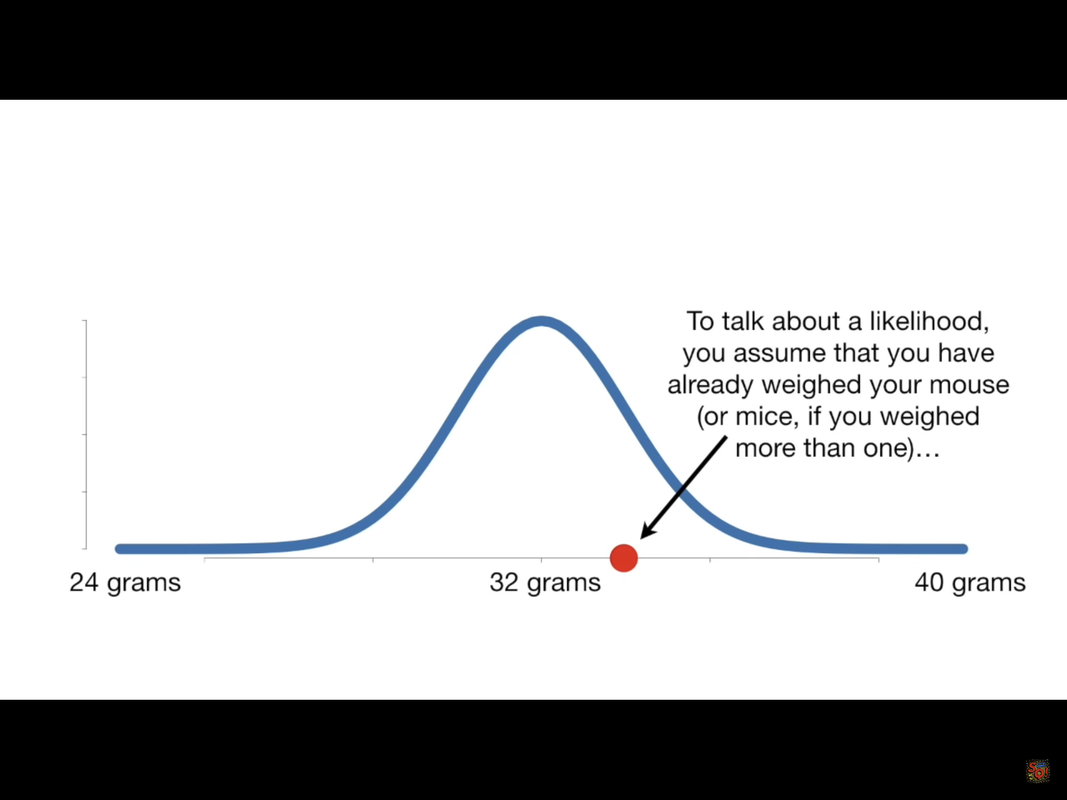
Likelihood
SUMMARY
REFERENCE
[출처] [수리통계학] 가능도는 확률과 어떻게 다르지? (가능도(Likelihood) VS. 확률(Probability))|작성자 PN
https://swjman.tistory.com/104
로봇공학을 공부하다 보면, 무조건 만나게 되는 개념 중에 가능도(likelihood)과 확률(Probability)라는 개념이 있다. (특히 Probabilisitic Robotics라는 엄청난 책도 있다.). 한 참 공부하다가 보면 이 기능도와 확률에 대해 헷갈리게 된다. 그래서 한번 복습할 겸 다시 한번 정리 해보고자 한다.
위키의 정의를 보면,
먼저 빈도학파의 관점에서 이야기 하며, 가능도 함수는 단순히 가능도라고 부를 수도 있고, 이것은 통계적인 모델의 파라미터의 함수를 말하는데 주어진 특정한 관찰된 데이터를 기반으로 한다. 가능도 함수들은 빈도 학파의 추론에서 주요한 역할을 하고 특히 통계치 집합으로부터 파라미터를 추정하는 방법으로 중요하다. 비공식적으로 “가능도”라는 것은 종종 “확률(Probability)”와 유사한 의미로 쓴다. 하지만 로봇공학에서는 이 두 가지 용어는 다른 의미를 지닌다.
확률이라고 하면, 주어진 모델 파라마티 값과 어떠한 관찰된 데이터에 대한 참조 없이, 랜덤 출력에 대한 일어날 뻔한 가능성이다.
즉, 로봇공학으로 이해하자면 x,y,z에 대한 관찰 데이터 값이 존재하지 않고, scale parameter도 존재하지 않지만 transition matrix 및 matrix relevant control input에 대한 모델을 통해 (x,y,z)의 변수 랜덤 출력 데이터 값을 가지고 상태에 대한 예측하는 것이다.
반면, 가능도라는 것은 주어진 특정한 관찰된 데이터를 기반으로 하여 모델 파라미터 값들이 될 뻔한 가능성이다.
즉 로봇공학으로 이해하자면 x,y,z 에 대한 관찰 값이 주어지고 이를 통해 scale parameter 및 모델 안에 존재하는 파라미터 값들을 예측하는 것이다.
그렇기 때문에 가능도와 확률의 차이는 명백하다. 위의 정의를 읽어 보면 알겠지만, 아예 대상 자체가 다르다. 확률의 경우에는 출력의 확률이다. 즉, x와 같은 랜덤 변수가 미지수가 될 것이다. 해당 랜덤 변수 x가 될 확률이 확률이고, 여기서 파라미터 값들은 다 주어진다고 본다. 그래서 연속 변수의 경우 아래와 같이 확률 밀도 함수가 확률에 대한 함수가 될 수 있겠다.
f(x|Θ)
그러면 가능도는 어떤가? 가능도의 경우에는 L이라고 따로 표기하며, 조건부의 순서가 확률과 반대인 것을 알 수 있다. 이번에는 x라는 랜덤 변수가 주어졌을 때, 세타 즉, 파라미터의 확률이 된다. 랜덤 변수가 주어진다는 것은 사실 전체 모집단에 대한 랜덤 변수를 모두 안다는 것은 불가능 하다. 그래서 위에 정의에서도 말했듯이, x는 일반적인 랜덤 변수가 아닌, 측정하거나, 알고 있는 샘플들에 해당한다. 이렇게 샘플이 있을 때, 해당 샘플이 있을 때, 파라미터들이 될 수 있는 확률이 가능도이다.
L(Θ|x)
이게 표기법 때문에 헷갈릴 수 있는데, 왜냐하면 가끔 이 둘이 수학적으로 같다고 하기 때문이다. 그런데 그것은 하나의 샘플 데이터에 대해서 이야기 한다면 같을 수 있겠지만, 보통은 하나의 샘플이 아닌 여러 개의 샘플 즉, n개의 샘플 데이터가 있는 상태에서 통계적 분석을 하게 된다. 따라서, 아래와 같은 형태가 제대로된 가능도의 형태가 된다.
무엇을 의미하는지를 잘 살펴보면, x가 의미하는 것은 여러 개의 샘플들이 되고, 각각의 샘플이 주어졌을때의 가능도를 모두 곱하게 된다. 앞에서 말했듯이, 샘플 하나에 대한 가능도는 확률과 같기 때문에(위의경우 연속 변수이니 확률 밀도 함수와 같다) 그래서 f라고 표기한 확률을 사용해서 가능도를 만들며, 앞에 곱하기 표시를 해서 각 샘플에 대해서 모두 곱하는 것이다. 여기서 왜 곱하기를 하는지 생각해보자. 그것은 다름 아닌, 아래와 같이 가능도가 샘플이 여러 개일 때, joint probability와 같게 되는데, 이 때, 각각의 샘플들의 확률들에 대해서 조인트로 일어날 확률이 가능도가 된다. 그런데 보통 샘플들을 취급할때, 독립성을 가정하기 때문에 조인트 확률은 단지 곱셈으로 대체가 되기 때문에 이러한 곱셈이 적용될 수 있다는 것도 기억하자.
EXAMPLES
Probability
Likelihood
SUMMARY
REFERENCE
[출처] [수리통계학] 가능도는 확률과 어떻게 다르지? (가능도(Likelihood) VS. 확률(Probability))|작성자 PN













Comments