Gaussian 방법을 이용한 Machine learning
20 Oct 2021 | calculus
가우시안이 누구인가
1777-1855에 활동안 독일의 수학자 이다.
3살때부터 아버지가 실수한 수학문제를 풀었다고 한다.(구라같음..)
7살때 등차 수열(arithmetic series)을 마스터 하였다고 한다.
대학에 들어오고 실용적인 수학을 연구를 하면서 많은 field에서 contribution을 하였다.(Fermat polygonal number theorem, Fermat’s Last Theorem, Descartes’s rule of signs, Kepler conjecture, Non-Euclidean geometries )
가우시안은 완벽주의자이고 하드워커이다. 완벽하게 작업이 끝나지 않은 것들은 퍼블리시를 절대 하지 않았다.
가우시안이 간단하게 누군지 궁금 한 이유는 공부를 하다보면 가우시안 이름이 들어간 공식이 엄청 많다. 도대체 뭐하는 사람인지 궁금하였고, 오늘에서야 조금 이해가 되었다.
Gaussian Process for Machine learning
Gaussian processes are a powerful algorithm for both regression and classification. Their greatest practical advantage is that they can give a reliable estimate of their own uncertainty.
before div into Gaussian Process. let me introduce where it used mostly these-day, in particular, machine learning.
What is machine learning?
Machine learning is using data we have (known as training data) to learn a function that we can use to make predictions about data we don’t have yet. The simplest example of this is linear regression, where we learn the slope and intercept of a line so we can predict the vertical position of points from their horizontal position. This is shown below, the training data are the blue points and the learnt function is the red line.
Machine learning is an extension of linear regression in a few ways. Firstly is that modern ML deals with much more complicated data, instead of learning a function to calculate a single number from another number like in linear regression we might be dealing with different inputs and outputs such as:
- The price of a house (output) dependent on its location, number of rooms, etc… (inputs)
- The content of an image (output) based on the intensities and colours of pixels in the image (inputs)
- The best move (output) based on the state of a board of Go (input)
- A higher resolution image (output) based on a low resolution image (input)
Secondly, modern ML uses much more powerful methods for extracting patterns of which deep learning is only one of many. Gaussian processes are another of these methods and their primary distinction(특별함) is their relation to uncertainty.
Thinking about uncertainty
Uncertainty can be represented as a set of possible outcomes and their respective(각각의) likelihood — called a probability distribution(http://hyperphysics.phy-astr.gsu.edu/hbase/Math/gaufcn.html)
The world around us is filled with uncertainty — we do not know exactly how long our commute will take or precisely what the weather will be at noon tomorrow. Some uncertainty is due to our lack of knowledge is intrinsic to the world no matter how much knowledge we have. Since we are unable to completely remove uncertainty from the universe we best have a good way of dealing with it. Probability distributions are exactly that and it turns out that these are the key to understanding Gaussian processes.
The most obvious example of a probability distribution is that of the outcome of rolling a fair 6-sided dice i.e. a one in six chance of any particular face.
This is an example of a discrete probability distributions as there are a finite number of possible outcomes. In the discrete case a probability distribution is just a list of possible outcomes and the chance of them occurring. In many real world scenarios a continuous probability distribution is more appropriate as the outcome could be any real number and example of one is explored in the next section.
Another key concept that will be useful later is sampling from a probability distribution. This means going from a set of possible outcomes to just one real outcome — rolling the dice in this example.
Bayesian inference(추론)
Bayesian inference might be an intimidating phrase but it boils down to just a method for updating our beliefs about the world based on evidence that we observe.
In Bayesian inference our beliefs about the world are typically represented as probability distributions and Bayes’ rule tells us how to update these probability distributions.
Bayesian statistics provides us the tools to update our beliefs (represented as probability distributions) based on new data
updating uncertainty and update and predict value
Let’s run through an illustrative example of Bayesian inference — we are going to adjust our beliefs about the height of Barack Obama based on some evidence.
Let’s consider that we’ve never heard of Barack Obama (bear with me), or at least we have no idea what his height is. However we do know he’s a male human being resident in the USA. Hence our belief about Obama’s height before seeing any evidence (in Bayesian terms this is our prior belief) should just be the distribution of heights of American males.
Now let’s pretend that Wikipedia doesn’t exist so we can’t just look up Obama’s height and instead observe some evidence in the form of a photo.
Our updated belief (posterior in Bayesian terms) looks something like this.
We can see that Obama is definitely taller than average, coming slightly above several other world leaders, however we can’t be quite sure how tall exactly. The probability distribution shown still reflects the small chance that Obama is average height and everyone else in the photo is unusually short.
슬램을 생각해 보면, 어떤 n-1 state에서 observation이나 motion model로 구축된 prior state에 n state에 여러 observation 데이터와 motion 데이터가 새로운 gaussian distribution을 형상하게 되는데, 이 두 gaussian distribution에서의 maximum liklehood 값을 찾아 n번째 상태를 추정하는 것이다. 그리고 guassian distribtuion을 update 한다.
What is a Gaussian process?
Now that we know how to represent uncertainty over numeric values such as height or the outcome of a dice roll we are ready to learn what a Gaussian process is.
A Gaussian process is a probability distribution over possible functions.
Since Gaussian processes let us describe probability distributions over functions we can use Bayes’ rule to update our distribution of functions by observing training data.
To reinforce this intuition I’ll run through an example of Bayesian inference with Gaussian processes which is exactly analogous to the example in the previous section. Instead of updating our belief about Obama’s height based on photos we’ll update our belief about an unknown function given some samples from that function.
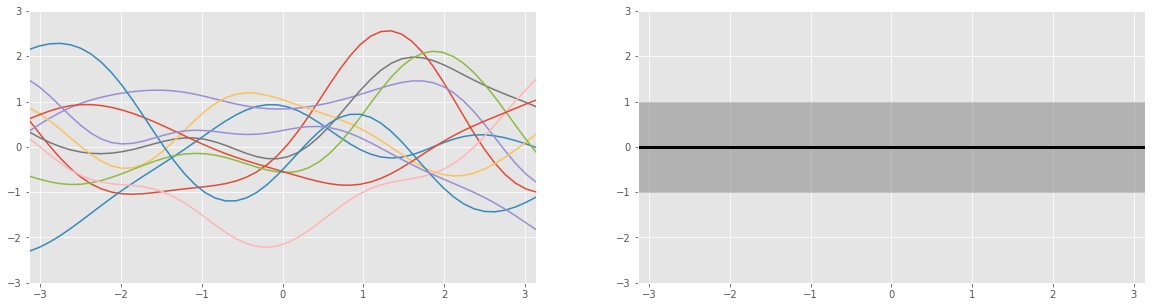
Our prior belief about the the unknown function is visualized above. On the right is the mean and standard deviation of our Gaussian process — we don’t have any knowledge about the function so the best guess for our mean is in the middle of the real numbers i.e. 0.
On the left each line is a sample from the distribution of functions and our lack of knowledge is reflected in the wide range of possible functions and diverse function shapes on display. Sampling from a Gaussian process is like rolling a dice but each time you get a different function, and there are an infinite number of possible functions that could result.
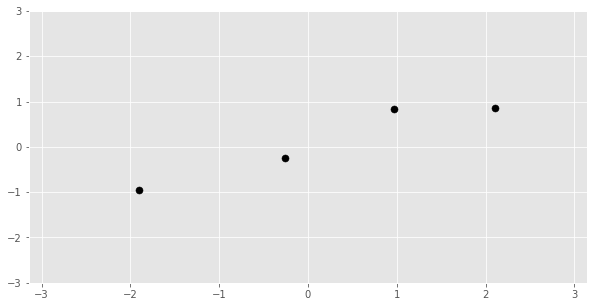
Instead of observing some photos of Obama we will instead observe some outputs of the unknown function at various points. For Gaussian processes our evidence is the training data.
Now that we’ve seen some evidence let’s use Bayes’ rule to update our belief about the function to get the posterior Gaussian process AKA our updated belief about the function we’re trying to fit.
Similarly to the narrowed distribution of possible heights of Obama what you can see is a narrower distribution of functions. The updated Gaussian process is constrained to the possible functions that fit our training data —the mean of our function intercepts all training points and so does every sampled function. We can also see that the standard deviation is higher away from our training data which reflects our lack of knowledge about these areas.
Advantages and disadvantages of GPs
Gaussian processes know what they don’t know
This sounds simple but many, if not most ML methods don’t share this. A key benefit is that the uncertainty of a fitted GP increases away from the training data — this is a direct consequence of GPs roots in probability and Bayesian inference.
Above we can see the classification functions learned by different methods on a simple task of separating blue and red dots. Note that two commonly used and powerful methods maintain high certainty of their predictions far from the training data — this could be linked to the phenomenon of adversarial examples where powerful classifiers give very wrong predictions for strange reasons. This characteristic of Gaussian processes is particularly relevant for identity verification and security critical uses as you want to be completely certain your models output is for a good reason.
Gaussian processes let you incorporate expert knowledge.
When you’re using a GP to model your problem you can shape your prior belief via the choice of kernel.
This lets you shape your fitted function in many different ways. The observant among you may have been wondering how Gaussian processes are ever supposed to generalize beyond their training data given the uncertainty property discussed above. Well the answer is that the generalization properties of GPs rest almost entirely within the choice of kernel.
Gaussian processes are computationally expensive.
Gaussian processes are a non-parametric method. Parametric approaches distill knowledge about the training data into a set of numbers. For linear regression this is just two numbers, the slope and the intercept, whereas other approaches like neural networks may have 10s of millions. This means that after they are trained the cost of making predictions is dependent only on the number of parameters.
However as Gaussian processes are non-parametric (although kernel hyperparameters blur the picture) they need to take into account the whole training data each time they make a prediction. This means not only that the training data has to be kept at inference time but also means that the computational cost of predictions scales (cubically!) with the number of training samples.
The future of Gaussian processes
The world of Gaussian processes will remain exciting for the foreseeable as research is being done to bring their probabilistic benefits to problems currently dominated by deep learning — sparse and minibatch Gaussian processes increase their scalability to large datasets while deep and convolutional Gaussian processes put high-dimensional and image data within reach. Watch this space.
KEY Process for machine learning
-
classification : two data value(train, valid)-> data input -> obtain mean -> variance -> standard deviation -> trained dataset -> trained gaussian distribution(gaussian model)(labels ex 0,1) -> input data to gaussian model -> get probability -> over certain threshold -> judge point label is 0, 1
-
Prediction : two data value(train, valid) -> data input -> obtained mean -> variance -> standard deviation -> trained dataset -> trained gaussian distribution -> input data to gaussian model -> get likelihood -> get obtained parameter -> update parameter
-
my study case : datas(height data on grid map) -> variance(obtained from consideration of sensor height variance) -> mean -> variance -> covariance matrix -> matrix decomposition(eigen value, egien vector) -> ellipes Rotation, ellipes lengh -> submap(ellipes) mean and weight -> center of ellipes -> probabilities(x,y) -> calculate weight by probabilities -> update upper bound and lower bound distribution by weight. -> update mean.
즉 uncertainty로 probability를 구하고, weight를 구하여 uncertainty를 고려한 weight를 mean에다가 업데이트 시켜준다.
정리
Uncertainty를 이용하는 것은 probability distribution을 구하는 것이다. likelihood, probability distribution function.
KNN -> nearlest point -> put current data in gaussian model(built by previous data)
REFERENCE
https://www.mathsisfun.com/data/standard-deviation.html
가우시안이 누구인가
1777-1855에 활동안 독일의 수학자 이다. 3살때부터 아버지가 실수한 수학문제를 풀었다고 한다.(구라같음..) 7살때 등차 수열(arithmetic series)을 마스터 하였다고 한다. 대학에 들어오고 실용적인 수학을 연구를 하면서 많은 field에서 contribution을 하였다.(Fermat polygonal number theorem, Fermat’s Last Theorem, Descartes’s rule of signs, Kepler conjecture, Non-Euclidean geometries ) 가우시안은 완벽주의자이고 하드워커이다. 완벽하게 작업이 끝나지 않은 것들은 퍼블리시를 절대 하지 않았다.
가우시안이 간단하게 누군지 궁금 한 이유는 공부를 하다보면 가우시안 이름이 들어간 공식이 엄청 많다. 도대체 뭐하는 사람인지 궁금하였고, 오늘에서야 조금 이해가 되었다.
Gaussian Process for Machine learning
Gaussian processes are a powerful algorithm for both regression and classification. Their greatest practical advantage is that they can give a reliable estimate of their own uncertainty.
before div into Gaussian Process. let me introduce where it used mostly these-day, in particular, machine learning.
What is machine learning?
Machine learning is using data we have (known as training data) to learn a function that we can use to make predictions about data we don’t have yet. The simplest example of this is linear regression, where we learn the slope and intercept of a line so we can predict the vertical position of points from their horizontal position. This is shown below, the training data are the blue points and the learnt function is the red line.
Machine learning is an extension of linear regression in a few ways. Firstly is that modern ML deals with much more complicated data, instead of learning a function to calculate a single number from another number like in linear regression we might be dealing with different inputs and outputs such as:
- The price of a house (output) dependent on its location, number of rooms, etc… (inputs)
- The content of an image (output) based on the intensities and colours of pixels in the image (inputs)
- The best move (output) based on the state of a board of Go (input)
- A higher resolution image (output) based on a low resolution image (input)
Secondly, modern ML uses much more powerful methods for extracting patterns of which deep learning is only one of many. Gaussian processes are another of these methods and their primary distinction(특별함) is their relation to uncertainty.
Thinking about uncertainty
Uncertainty can be represented as a set of possible outcomes and their respective(각각의) likelihood — called a probability distribution(http://hyperphysics.phy-astr.gsu.edu/hbase/Math/gaufcn.html)
The world around us is filled with uncertainty — we do not know exactly how long our commute will take or precisely what the weather will be at noon tomorrow. Some uncertainty is due to our lack of knowledge is intrinsic to the world no matter how much knowledge we have. Since we are unable to completely remove uncertainty from the universe we best have a good way of dealing with it. Probability distributions are exactly that and it turns out that these are the key to understanding Gaussian processes.
The most obvious example of a probability distribution is that of the outcome of rolling a fair 6-sided dice i.e. a one in six chance of any particular face.
This is an example of a discrete probability distributions as there are a finite number of possible outcomes. In the discrete case a probability distribution is just a list of possible outcomes and the chance of them occurring. In many real world scenarios a continuous probability distribution is more appropriate as the outcome could be any real number and example of one is explored in the next section. Another key concept that will be useful later is sampling from a probability distribution. This means going from a set of possible outcomes to just one real outcome — rolling the dice in this example.
Bayesian inference(추론)
Bayesian inference might be an intimidating phrase but it boils down to just a method for updating our beliefs about the world based on evidence that we observe.
In Bayesian inference our beliefs about the world are typically represented as probability distributions and Bayes’ rule tells us how to update these probability distributions.
Bayesian statistics provides us the tools to update our beliefs (represented as probability distributions) based on new data
updating uncertainty and update and predict value
Let’s run through an illustrative example of Bayesian inference — we are going to adjust our beliefs about the height of Barack Obama based on some evidence.
Let’s consider that we’ve never heard of Barack Obama (bear with me), or at least we have no idea what his height is. However we do know he’s a male human being resident in the USA. Hence our belief about Obama’s height before seeing any evidence (in Bayesian terms this is our prior belief) should just be the distribution of heights of American males.
Now let’s pretend that Wikipedia doesn’t exist so we can’t just look up Obama’s height and instead observe some evidence in the form of a photo.
Our updated belief (posterior in Bayesian terms) looks something like this.
We can see that Obama is definitely taller than average, coming slightly above several other world leaders, however we can’t be quite sure how tall exactly. The probability distribution shown still reflects the small chance that Obama is average height and everyone else in the photo is unusually short.
슬램을 생각해 보면, 어떤 n-1 state에서 observation이나 motion model로 구축된 prior state에 n state에 여러 observation 데이터와 motion 데이터가 새로운 gaussian distribution을 형상하게 되는데, 이 두 gaussian distribution에서의 maximum liklehood 값을 찾아 n번째 상태를 추정하는 것이다. 그리고 guassian distribtuion을 update 한다.
What is a Gaussian process?
Now that we know how to represent uncertainty over numeric values such as height or the outcome of a dice roll we are ready to learn what a Gaussian process is.
A Gaussian process is a probability distribution over possible functions.
Since Gaussian processes let us describe probability distributions over functions we can use Bayes’ rule to update our distribution of functions by observing training data.
To reinforce this intuition I’ll run through an example of Bayesian inference with Gaussian processes which is exactly analogous to the example in the previous section. Instead of updating our belief about Obama’s height based on photos we’ll update our belief about an unknown function given some samples from that function.
Our prior belief about the the unknown function is visualized above. On the right is the mean and standard deviation of our Gaussian process — we don’t have any knowledge about the function so the best guess for our mean is in the middle of the real numbers i.e. 0.
On the left each line is a sample from the distribution of functions and our lack of knowledge is reflected in the wide range of possible functions and diverse function shapes on display. Sampling from a Gaussian process is like rolling a dice but each time you get a different function, and there are an infinite number of possible functions that could result.
Instead of observing some photos of Obama we will instead observe some outputs of the unknown function at various points. For Gaussian processes our evidence is the training data.
Now that we’ve seen some evidence let’s use Bayes’ rule to update our belief about the function to get the posterior Gaussian process AKA our updated belief about the function we’re trying to fit.
Similarly to the narrowed distribution of possible heights of Obama what you can see is a narrower distribution of functions. The updated Gaussian process is constrained to the possible functions that fit our training data —the mean of our function intercepts all training points and so does every sampled function. We can also see that the standard deviation is higher away from our training data which reflects our lack of knowledge about these areas.
Advantages and disadvantages of GPs
Gaussian processes know what they don’t know
This sounds simple but many, if not most ML methods don’t share this. A key benefit is that the uncertainty of a fitted GP increases away from the training data — this is a direct consequence of GPs roots in probability and Bayesian inference.
Above we can see the classification functions learned by different methods on a simple task of separating blue and red dots. Note that two commonly used and powerful methods maintain high certainty of their predictions far from the training data — this could be linked to the phenomenon of adversarial examples where powerful classifiers give very wrong predictions for strange reasons. This characteristic of Gaussian processes is particularly relevant for identity verification and security critical uses as you want to be completely certain your models output is for a good reason.
Gaussian processes let you incorporate expert knowledge.
When you’re using a GP to model your problem you can shape your prior belief via the choice of kernel.
This lets you shape your fitted function in many different ways. The observant among you may have been wondering how Gaussian processes are ever supposed to generalize beyond their training data given the uncertainty property discussed above. Well the answer is that the generalization properties of GPs rest almost entirely within the choice of kernel.
Gaussian processes are computationally expensive.
Gaussian processes are a non-parametric method. Parametric approaches distill knowledge about the training data into a set of numbers. For linear regression this is just two numbers, the slope and the intercept, whereas other approaches like neural networks may have 10s of millions. This means that after they are trained the cost of making predictions is dependent only on the number of parameters.
However as Gaussian processes are non-parametric (although kernel hyperparameters blur the picture) they need to take into account the whole training data each time they make a prediction. This means not only that the training data has to be kept at inference time but also means that the computational cost of predictions scales (cubically!) with the number of training samples.
The future of Gaussian processes
The world of Gaussian processes will remain exciting for the foreseeable as research is being done to bring their probabilistic benefits to problems currently dominated by deep learning — sparse and minibatch Gaussian processes increase their scalability to large datasets while deep and convolutional Gaussian processes put high-dimensional and image data within reach. Watch this space.
KEY Process for machine learning
-
classification : two data value(train, valid)-> data input -> obtain mean -> variance -> standard deviation -> trained dataset -> trained gaussian distribution(gaussian model)(labels ex 0,1) -> input data to gaussian model -> get probability -> over certain threshold -> judge point label is 0, 1
-
Prediction : two data value(train, valid) -> data input -> obtained mean -> variance -> standard deviation -> trained dataset -> trained gaussian distribution -> input data to gaussian model -> get likelihood -> get obtained parameter -> update parameter
-
my study case : datas(height data on grid map) -> variance(obtained from consideration of sensor height variance) -> mean -> variance -> covariance matrix -> matrix decomposition(eigen value, egien vector) -> ellipes Rotation, ellipes lengh -> submap(ellipes) mean and weight -> center of ellipes -> probabilities(x,y) -> calculate weight by probabilities -> update upper bound and lower bound distribution by weight. -> update mean.
즉 uncertainty로 probability를 구하고, weight를 구하여 uncertainty를 고려한 weight를 mean에다가 업데이트 시켜준다.
정리
Uncertainty를 이용하는 것은 probability distribution을 구하는 것이다. likelihood, probability distribution function.
KNN -> nearlest point -> put current data in gaussian model(built by previous data)
REFERENCE
https://www.mathsisfun.com/data/standard-deviation.html







Comments