법선 벡터을 이용한 어플리케이션 및 방법
22 Oct 2021 | calculus
법선 벡터(normal vector)를 이용하여 컴퓨터 비전에 많은 어플리케이션에 사용이 된다. 주로 사용되는 어플리케이션은 Ground Segementation일 것이다.
법선 벡터는 혼자 만들 수 없다. 주변(neighbor) 포인트들과 결합이 되서 만들어야 된다. 또한 Dimension도 최소 2D 이여야만 한다. 그래야만 법선 방향을 알 수 있기 떄문이다.
2D에서 2개의 포인트로 법선벡터를 만들수 있는데 모양을 아래와 같게 된다. 2D 에서는 최소 2개의 점이 필요하게 되고 외적을 통해 법선 벡터를 만들 수 있다.
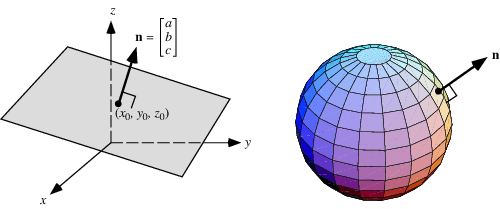
3D에서는 최소 3개의 포인트를 필요하게 되고 외적을 통해 법선 벡터를 만들 수 있다.
3D에서의 법선 벡터를 구하는 것은 여러 포인트와 컨넥트가 되어있기 떄문에 다른 말로 Normal Surface라고도 할 수 있다.
법선 벡터가 중요한 이유는 우리는 가지고 있는 벡터들을 통해서 방향성을 얻을 수 있다. (법선 벡터)
앞서 말한 ground segementation같은 경우 벡터들을에 대한 normal vector를 구할 수 있는데, 이를 통해서 surface에 대한 방향을 구할 수 있다.
얻어진 normal surface(normal vector)에는 곡률(curvature)을 나타낼 수 있는데, Ground Plane은 항상 평평함으로써 curvature에 대한 제약 조건과 normal vector의 방향으로 Ground Segementation을 할 수 있다.
즉 법선 벡터를 구하는 이유는 벡터에 대한 방향성을 알 수 있기 떄문에, 이를 통해서 객체와 바닥을 구분할 수 있다.
법선벡터 구하는 방법 및 프로세스
1. Covaraince Matrix 방법
첫번째로는 Covariance Matrix를 이용하여서 법선 벡터(Normal Surface)를 구할 수 있다.
예로 많은 데이터가 3D상에 분포가 되어 있다고 가정을 한다면, 우리는 KNN같은 nearlest Search 알고리즘이나, 특정 Region(Submap or ellipes)를 지정을 하여서 포인트들에 대한 집합을 찾는다.
포인트들에 대한 집합을 찾았으면, 집합에 대한 Mean값을 찾고 Variance를 이용한 Standard Deivation(Square Variance)을 만들게 된다. 만들어진 Standard Deviation을 통해 Covariance Matrix를 아래와 같이 구할 수 있다.
Covariance Matrix(Information Matrix) =
std_xx std_xy std_xz
std_yx std_yy std_yz
std_zx std_zy std_zz
구해진 Covariance Matrix를 SVD(Singularity value decomposition) 및 PCA를 통해서 EigenValue와 EigenVector를 구하게 된다.
얻어진 EigenValue와 EigenVector를 통해 우리는 법선 벡터, 즉 Normal Surface에대한 방향을 구할 수 있다. EigenValue의 값이 2개는 크거나 같고 하나가 작다면 Plane이고, EigenVector가 1나가 크고 2개가 작다면 라인, 3개가 작다면 Point로 간주하게 된다.
이떄 보통 우리는 Normal Vector의 방향을 나타낼떄는 Eigenvalue가 작은 것을 사용을 하여서 방향을 나타낸다.
이를 통해 데이터에 대한 법선 벡터(Normal Surface)를 알 수 있다
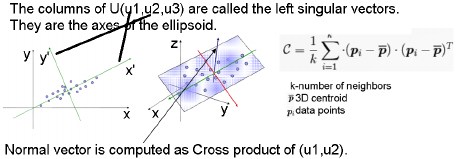
Principle axes of ellipse point in directions of corresponding eigenvectors
So: surface normal is in the direction of the Eigenvector corresponding to the smallest Eigenvalue of
핵심 및 활용
http://www.ccs.neu.edu/home/rplatt/cs5335_fall2016/slides/point_clouds.pdf
Centet point의 eigenvector와 EigenValue로 법선 벡터를 구할 수 있다.
2. Cross Product 외적 방법
쉽게 외적을 통해서 Normal Vector를 구할 수 있다. 3디라면 최소 3개의 포인트를 통해서 구할 수 있다. 외적을 통해서 얻어진 Normal Vector들은 Covariance Matrix와 마찬가지로 2개의 벡터가 크거나 같고, 하나가 작으면 Plane, 1개의 벡터가 크고 2개의 Plane이 작다면 line, 3다 작으면 점이다.외적을 통해 얻어진 normal vector가 되며 비율을 통해서 포인트의 특징 (Shape) 결정을 할 수 있다. 보통 작은 벡터가 Normal Vector로 간주 된다.(Min Vector), length가 긴것(큰 벡터)들은 plane을 만들게 된다
비교
Covariance를 사용하는 방법은 Cost 하지만 정확하다. Cross Product을 사용하면 계산이 쉽지만 노이즈가 많을 수 있다.
법선 벡터(normal vector)를 이용하여 컴퓨터 비전에 많은 어플리케이션에 사용이 된다. 주로 사용되는 어플리케이션은 Ground Segementation일 것이다.
법선 벡터는 혼자 만들 수 없다. 주변(neighbor) 포인트들과 결합이 되서 만들어야 된다. 또한 Dimension도 최소 2D 이여야만 한다. 그래야만 법선 방향을 알 수 있기 떄문이다.
2D에서 2개의 포인트로 법선벡터를 만들수 있는데 모양을 아래와 같게 된다. 2D 에서는 최소 2개의 점이 필요하게 되고 외적을 통해 법선 벡터를 만들 수 있다.
3D에서는 최소 3개의 포인트를 필요하게 되고 외적을 통해 법선 벡터를 만들 수 있다.
3D에서의 법선 벡터를 구하는 것은 여러 포인트와 컨넥트가 되어있기 떄문에 다른 말로 Normal Surface라고도 할 수 있다.
법선 벡터가 중요한 이유는 우리는 가지고 있는 벡터들을 통해서 방향성을 얻을 수 있다. (법선 벡터)
앞서 말한 ground segementation같은 경우 벡터들을에 대한 normal vector를 구할 수 있는데, 이를 통해서 surface에 대한 방향을 구할 수 있다.
얻어진 normal surface(normal vector)에는 곡률(curvature)을 나타낼 수 있는데, Ground Plane은 항상 평평함으로써 curvature에 대한 제약 조건과 normal vector의 방향으로 Ground Segementation을 할 수 있다.
즉 법선 벡터를 구하는 이유는 벡터에 대한 방향성을 알 수 있기 떄문에, 이를 통해서 객체와 바닥을 구분할 수 있다.
법선벡터 구하는 방법 및 프로세스
1. Covaraince Matrix 방법
첫번째로는 Covariance Matrix를 이용하여서 법선 벡터(Normal Surface)를 구할 수 있다.
예로 많은 데이터가 3D상에 분포가 되어 있다고 가정을 한다면, 우리는 KNN같은 nearlest Search 알고리즘이나, 특정 Region(Submap or ellipes)를 지정을 하여서 포인트들에 대한 집합을 찾는다.
포인트들에 대한 집합을 찾았으면, 집합에 대한 Mean값을 찾고 Variance를 이용한 Standard Deivation(Square Variance)을 만들게 된다. 만들어진 Standard Deviation을 통해 Covariance Matrix를 아래와 같이 구할 수 있다.
Covariance Matrix(Information Matrix) =
std_xx std_xy std_xz
std_yx std_yy std_yz
std_zx std_zy std_zz
구해진 Covariance Matrix를 SVD(Singularity value decomposition) 및 PCA를 통해서 EigenValue와 EigenVector를 구하게 된다.
얻어진 EigenValue와 EigenVector를 통해 우리는 법선 벡터, 즉 Normal Surface에대한 방향을 구할 수 있다. EigenValue의 값이 2개는 크거나 같고 하나가 작다면 Plane이고, EigenVector가 1나가 크고 2개가 작다면 라인, 3개가 작다면 Point로 간주하게 된다.
이떄 보통 우리는 Normal Vector의 방향을 나타낼떄는 Eigenvalue가 작은 것을 사용을 하여서 방향을 나타낸다.
이를 통해 데이터에 대한 법선 벡터(Normal Surface)를 알 수 있다
Principle axes of ellipse point in directions of corresponding eigenvectors
So: surface normal is in the direction of the Eigenvector corresponding to the smallest Eigenvalue of
핵심 및 활용 http://www.ccs.neu.edu/home/rplatt/cs5335_fall2016/slides/point_clouds.pdf
Centet point의 eigenvector와 EigenValue로 법선 벡터를 구할 수 있다.
2. Cross Product 외적 방법
쉽게 외적을 통해서 Normal Vector를 구할 수 있다. 3디라면 최소 3개의 포인트를 통해서 구할 수 있다. 외적을 통해서 얻어진 Normal Vector들은 Covariance Matrix와 마찬가지로 2개의 벡터가 크거나 같고, 하나가 작으면 Plane, 1개의 벡터가 크고 2개의 Plane이 작다면 line, 3다 작으면 점이다.외적을 통해 얻어진 normal vector가 되며 비율을 통해서 포인트의 특징 (Shape) 결정을 할 수 있다. 보통 작은 벡터가 Normal Vector로 간주 된다.(Min Vector), length가 긴것(큰 벡터)들은 plane을 만들게 된다
비교
Covariance를 사용하는 방법은 Cost 하지만 정확하다. Cross Product을 사용하면 계산이 쉽지만 노이즈가 많을 수 있다.




Comments