64. Maximal Square [ 어려움 ]
12 Aug 2020 | Daily Algorithms
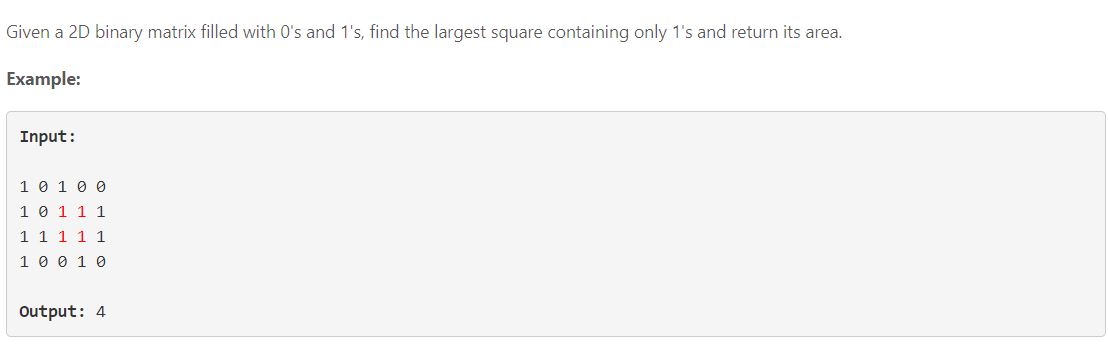
- To appy DP, we define the state as the maximal size (square = size * size) of the square that can be formed till point (i, j), denoted as dp[i][j]
-
For the topmost row (i = 0) and the leftmost column (j = 0), we have dp[i][j] = matrix[i][j] - ‘0’, meaning that it can at most form a square of size 1 when the matrix has a ‘1’ in that cell.
- When i > 0 and j > 0, if matrix[i][j] = ‘0’, then dp[i][j] = 0 since no square will be able to contain the ‘0’ at that cell. If matrix[i][j] = ‘1’, we will have dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1, which means that the square will be limited by its left, upper and upper-left neighbors.
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if(matrix.empty())
return 0;
int m = matrix.size();
int n = matrix[0].size();
int sz = 0 ;
vector<vector<int>> dp(m, vector<int>(n,0));// mxn with elment value 0;
for(int i = 0; i<m; i++)
{
for(int j =0;j<n;j++)
{
if(!i || !j || matrix[i][j] == '0')
{
dp[i][j] = matrix[i][j] - '0';
// 만약 i와 j가 0일경우 즉 square 테두리 형성과, 스퀘어 안에 0이 있을경우도 square안에 넣음
}
else
{
//if matrix[i][j] = '1'
// square will be limited by its left, upper and upper-left
dp[i][j]= min(dp[i-1][j-1],min(dp[i-1][j],dp[i][j-1]))+1;
}
sz = max(dp[i][j],sz);
}
}
return sz*sz;
}
};
- To appy DP, we define the state as the maximal size (square = size * size) of the square that can be formed till point (i, j), denoted as dp[i][j]
-
For the topmost row (i = 0) and the leftmost column (j = 0), we have dp[i][j] = matrix[i][j] - ‘0’, meaning that it can at most form a square of size 1 when the matrix has a ‘1’ in that cell.
- When i > 0 and j > 0, if matrix[i][j] = ‘0’, then dp[i][j] = 0 since no square will be able to contain the ‘0’ at that cell. If matrix[i][j] = ‘1’, we will have dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1, which means that the square will be limited by its left, upper and upper-left neighbors.
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if(matrix.empty())
return 0;
int m = matrix.size();
int n = matrix[0].size();
int sz = 0 ;
vector<vector<int>> dp(m, vector<int>(n,0));// mxn with elment value 0;
for(int i = 0; i<m; i++)
{
for(int j =0;j<n;j++)
{
if(!i || !j || matrix[i][j] == '0')
{
dp[i][j] = matrix[i][j] - '0';
// 만약 i와 j가 0일경우 즉 square 테두리 형성과, 스퀘어 안에 0이 있을경우도 square안에 넣음
}
else
{
//if matrix[i][j] = '1'
// square will be limited by its left, upper and upper-left
dp[i][j]= min(dp[i-1][j-1],min(dp[i-1][j],dp[i][j-1]))+1;
}
sz = max(dp[i][j],sz);
}
}
return sz*sz;
}
};

Comments