1. Queue Stack(First in First Out data)
01 Nov 2019 | Data structure_1
1. Introduction
- We may access a random element by index in Array. However, we might want to restrict the processing order in some cases.
- we introduce two different processing orders, First-in-First-out and Last-in-First-out and its two corresponding linear data structures, Queue and Stack.
- We go through the definition, implementation and built-in functions for each data structure.
- Then, we focus more on the practical applications of these two data structures.
- By completing this card, you should be able to:
- Understand the principle of the processing orders of FIFO and LIFO
- Implement these two data structures
- Be familiar with the built-in queue and stack structure
- Solve basic queue-related problems, especially BFS(Breadth-Frist Search)
- Solve basic stack-related problems problems
- Understand how system stack helps you when you solve problems using DFS(Depth-First Search) and other recursion algorithms
2. Queue: First-in-first-out Data Structure
- The goal of this is to help you
- Understand the definition of FIFO and queue
- Be able to implement a queue by yourself
- Be familiar with the built-in queue structure
- Use queue to solve simple problems
First-in-first-out Data Structure
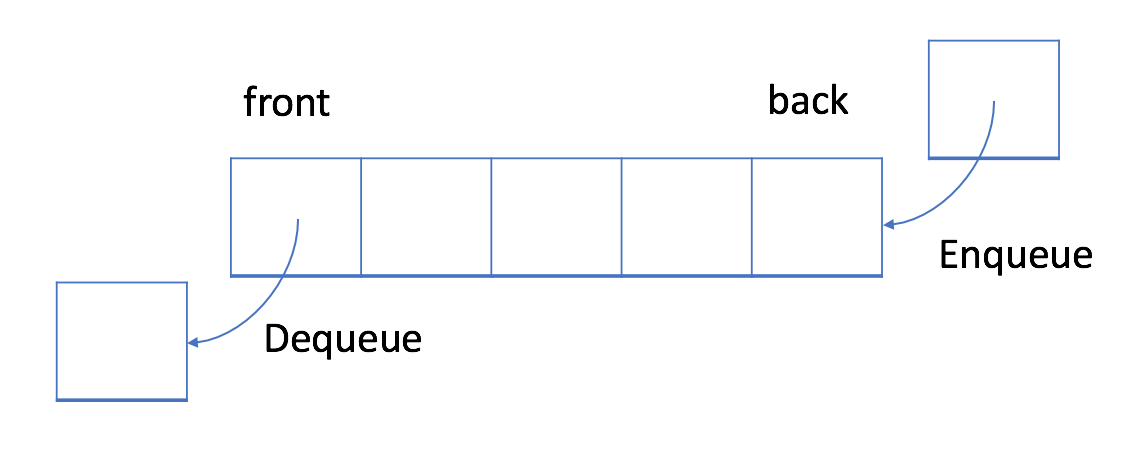
- In a FIFO data structure, the first element added to the queue will be processed first.
- As shown in the picture above, the queue is a typical FIFO data stucture. The insert operation is also called enqueue(排队) and the new element is always added at the end of the queue.
- The delete operation is called dequeue.
- you are only allowed to remove the first element
Exampe - Queue
- Enqueue: you can click Enqueue below to see how a new element 6 is added to the queue.
<img src=”https://i.postimg.cc/tTTfwGV3/screen-shot-2018-05-02-at-172840.png” width=”500px”
- Dequeue: you can click Dequeue below to see which element will be removed.
<img src=”https://i.postimg.cc/zDdWqZHL/screen-shot-2018-05-02-at-175409.png” width=”500px”
Circular Queue
- Previously, we have provided a straightforward but inefficient implementation of queue.
- A more efficient way is to use a circular queue. Specifically, we may use a fixed-size array and two pointers to indicate the starting position and the ending position.
- And the goal is to reuse the wasted storage we mentioned previously.
- Let’s take a look at an example to see how a circular queue works. You should pay attention to the strategy we use to enqueue or dequeue an element
https://leetcode.com/explore/learn/card/queue-stack/228/first-in-first-out-data-structure/1396/
- Review the animation carefully to figure out the strategy we use to check if a queue is empty or full.
- For the next exercise, we will let you try to implement the circular queue by yourself and provide a solution later.
Design Circular Queue
- Design your implementation of the circular queue.
- The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle and the last position is connected back to the first position to make a circle.
- It is also called “Ring Buffer”
- One of the benefits of the circular queue is that we can make use of the spaces in front of the queue.
- In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue.
- But using the circular queue, we can use the space to store new values.
- Your implementation should support following operations:
- MyCircularQueue(k): Constructor, set the size of the queue to be k.
- Front: Get the front item from the queue. If the queue is empty, return -1.
- Rear: Get the last item from the queue. If the queue is empty, return -1.
- enQueue(value): Insert an element into the circular queue. Return true if the operation is successful.
- deQueue(): Delete an element from the circular queue. Return true if the operation is successful.
- isEmpty(): Checks whether the circular queue is empty or not.
- isFull(): Checks whether the circular queue is full or not.
Example:
MyCircularQueue circularQueue = new MyCircularQueue(3); // set the size to be 3
circularQueue.enQueue(1); // return true
circularQueue.enQueue(2); // return true
circularQueue.enQueue(3); // return true
circularQueue.enQueue(4); // return false, the queue is full
circularQueue.Rear(); // return 3
circularQueue.isFull(); // return true
circularQueue.deQueue(); // return true
circularQueue.enQueue(4); // return true
circularQueue.Rear(); // return 4
- Note:
- All values will be in the range of [0, 1000].
- The number of operations will be in the range of [1, 1000].
- Please do not use the built-in Queue library.
C++ implement manually
class MyCircularQueue{
private:
vector<int> data;
int head;
int tail;
int size;
public:
// initialize our data structure here. set the size of the queue to be k.
MyCircularQueue(int k){
data.resize(k);
head = -1;
tail = -1;
size = k;
}
// Insert an element into the circular queue. Return true if the operation is successful.
bool enQueue(int value){
if (isFull()){
return false;
}
if (isEmpty()){
head = 0;
}
tail = (tail + 1) % size;
data[tail] = value;
return true;
}
bool deQueue(){
if (isEmpty()){
return false;
}
if (head == tail){
head = -1;
tail = -1;
return true;
}
head = (head + 1 ) % size;
return true;
}
// get the front item from the queue.
int Front(){
if (isEmpty()){
return -1;
}
return data[head];
}
int Rear(){
if (isEmpty()){
return -1;
}
return data[tail];
}
/** Checks whether the circular queue is empty or not. */
bool isEmpty() {
return head == -1;
}
/** Checks whether the circular queue is full or not. */
bool isFull() {
return ((tail + 1) % size) == head;
}
}
Queue - Usage
Queue - Usage(Library)
#include <iostream>
int main() {
// 1. Initialize a queue.
queue<int> q;
// 2. Push new element.
q.push(5);
q.push(13);
q.push(8);
q.push(6);
// 3. Check if queue is empty.
if (q.empty()) {
cout << "Queue is empty!" << endl;
return 0;
}
// 4. Pop an element.
q.pop();
// 5. Get the first element.
cout << "The first element is: " << q.front() << endl;
// 6. Get the last element.
cout << "The last element is: " << q.back() << endl;
// 7. Get the size of the queue.
cout << "The size is: " << q.size() << endl;
}
Moving Average from Data stream
- Given a stream of integers and a window size, calculate the moving average of all integers in the sliding window.
example
MovingAverage m = new MovingAverage(3);
m.next(1) = 1
m.next(10) = (1 + 10) / 2
m.next(3) = (1 + 10 + 3) / 3
m.next(5) = (10 + 3 + 5) / 3
C++
class MovingAverage {
public:
// Initialize your data structure here.
double runningTotal;
unsigned int windowSize;
std::queue<int> buffer;
MovingAverage(unsigned int inputSize) {
// initialize value
runningTotal = 0.0;
windowSize = inputSize;
}
double next(int inputValue) {
// check if buffer is full
if (buffer.size() == windowSize)
{
// subtract front value from running total
runningTotal -= buffer.front();
// delete value from front of std::queue
buffer.pop();
}
// add new value
buffer.push(inputValue);
// update running total
runningTotal += inputValue;
// calculate average
return static_cast<double>(runningTotal / buffer.size());
}
};
/**
* Your MovingAverage object will be instantiated and called as such:
* MovingAverage* obj = new MovingAverage(size);
* double param_1 = obj->next(val);
*/
static_cast
- static_cast<바꾸려고 하는="" 타입="">(대상);
- static_cast<new_type<(expression)
- 실수와 정수, 열거형과 정수형, 실수와 실수 사이의 변환을 허용
Reference
https://leetcode.com/
1. Introduction
- We may access a random element by index in Array. However, we might want to restrict the processing order in some cases.
- we introduce two different processing orders, First-in-First-out and Last-in-First-out and its two corresponding linear data structures, Queue and Stack.
- We go through the definition, implementation and built-in functions for each data structure.
- Then, we focus more on the practical applications of these two data structures.
- By completing this card, you should be able to:
- Understand the principle of the processing orders of FIFO and LIFO
- Implement these two data structures
- Be familiar with the built-in queue and stack structure
- Solve basic queue-related problems, especially BFS(Breadth-Frist Search)
- Solve basic stack-related problems problems
- Understand how system stack helps you when you solve problems using DFS(Depth-First Search) and other recursion algorithms
2. Queue: First-in-first-out Data Structure
- The goal of this is to help you
- Understand the definition of FIFO and queue
- Be able to implement a queue by yourself
- Be familiar with the built-in queue structure
- Use queue to solve simple problems
First-in-first-out Data Structure
- In a FIFO data structure, the first element added to the queue will be processed first.
- As shown in the picture above, the queue is a typical FIFO data stucture. The insert operation is also called enqueue(排队) and the new element is always added at the end of the queue.
- The delete operation is called dequeue.
- you are only allowed to remove the first element
Exampe - Queue
- Enqueue: you can click Enqueue below to see how a new element 6 is added to the queue.
<img src=”https://i.postimg.cc/tTTfwGV3/screen-shot-2018-05-02-at-172840.png” width=”500px”
- Dequeue: you can click Dequeue below to see which element will be removed.
<img src=”https://i.postimg.cc/zDdWqZHL/screen-shot-2018-05-02-at-175409.png” width=”500px”
Circular Queue
- Previously, we have provided a straightforward but inefficient implementation of queue.
- A more efficient way is to use a circular queue. Specifically, we may use a fixed-size array and two pointers to indicate the starting position and the ending position.
- And the goal is to reuse the wasted storage we mentioned previously.
- Let’s take a look at an example to see how a circular queue works. You should pay attention to the strategy we use to enqueue or dequeue an element
https://leetcode.com/explore/learn/card/queue-stack/228/first-in-first-out-data-structure/1396/
- Review the animation carefully to figure out the strategy we use to check if a queue is empty or full.
- For the next exercise, we will let you try to implement the circular queue by yourself and provide a solution later.
Design Circular Queue
- Design your implementation of the circular queue.
- The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle and the last position is connected back to the first position to make a circle.
- It is also called “Ring Buffer”
- One of the benefits of the circular queue is that we can make use of the spaces in front of the queue.
- In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue.
- But using the circular queue, we can use the space to store new values.
- Your implementation should support following operations:
- MyCircularQueue(k): Constructor, set the size of the queue to be k.
- Front: Get the front item from the queue. If the queue is empty, return -1.
- Rear: Get the last item from the queue. If the queue is empty, return -1.
- enQueue(value): Insert an element into the circular queue. Return true if the operation is successful.
- deQueue(): Delete an element from the circular queue. Return true if the operation is successful.
- isEmpty(): Checks whether the circular queue is empty or not.
- isFull(): Checks whether the circular queue is full or not.
Example:
MyCircularQueue circularQueue = new MyCircularQueue(3); // set the size to be 3
circularQueue.enQueue(1); // return true
circularQueue.enQueue(2); // return true
circularQueue.enQueue(3); // return true
circularQueue.enQueue(4); // return false, the queue is full
circularQueue.Rear(); // return 3
circularQueue.isFull(); // return true
circularQueue.deQueue(); // return true
circularQueue.enQueue(4); // return true
circularQueue.Rear(); // return 4
- Note:
- All values will be in the range of [0, 1000].
- The number of operations will be in the range of [1, 1000].
- Please do not use the built-in Queue library.
C++ implement manually
class MyCircularQueue{
private:
vector<int> data;
int head;
int tail;
int size;
public:
// initialize our data structure here. set the size of the queue to be k.
MyCircularQueue(int k){
data.resize(k);
head = -1;
tail = -1;
size = k;
}
// Insert an element into the circular queue. Return true if the operation is successful.
bool enQueue(int value){
if (isFull()){
return false;
}
if (isEmpty()){
head = 0;
}
tail = (tail + 1) % size;
data[tail] = value;
return true;
}
bool deQueue(){
if (isEmpty()){
return false;
}
if (head == tail){
head = -1;
tail = -1;
return true;
}
head = (head + 1 ) % size;
return true;
}
// get the front item from the queue.
int Front(){
if (isEmpty()){
return -1;
}
return data[head];
}
int Rear(){
if (isEmpty()){
return -1;
}
return data[tail];
}
/** Checks whether the circular queue is empty or not. */
bool isEmpty() {
return head == -1;
}
/** Checks whether the circular queue is full or not. */
bool isFull() {
return ((tail + 1) % size) == head;
}
}
Queue - Usage
Queue - Usage(Library)
#include <iostream>
int main() {
// 1. Initialize a queue.
queue<int> q;
// 2. Push new element.
q.push(5);
q.push(13);
q.push(8);
q.push(6);
// 3. Check if queue is empty.
if (q.empty()) {
cout << "Queue is empty!" << endl;
return 0;
}
// 4. Pop an element.
q.pop();
// 5. Get the first element.
cout << "The first element is: " << q.front() << endl;
// 6. Get the last element.
cout << "The last element is: " << q.back() << endl;
// 7. Get the size of the queue.
cout << "The size is: " << q.size() << endl;
}
Moving Average from Data stream
- Given a stream of integers and a window size, calculate the moving average of all integers in the sliding window.
example
MovingAverage m = new MovingAverage(3);
m.next(1) = 1
m.next(10) = (1 + 10) / 2
m.next(3) = (1 + 10 + 3) / 3
m.next(5) = (10 + 3 + 5) / 3
C++
class MovingAverage {
public:
// Initialize your data structure here.
double runningTotal;
unsigned int windowSize;
std::queue<int> buffer;
MovingAverage(unsigned int inputSize) {
// initialize value
runningTotal = 0.0;
windowSize = inputSize;
}
double next(int inputValue) {
// check if buffer is full
if (buffer.size() == windowSize)
{
// subtract front value from running total
runningTotal -= buffer.front();
// delete value from front of std::queue
buffer.pop();
}
// add new value
buffer.push(inputValue);
// update running total
runningTotal += inputValue;
// calculate average
return static_cast<double>(runningTotal / buffer.size());
}
};
/**
* Your MovingAverage object will be instantiated and called as such:
* MovingAverage* obj = new MovingAverage(size);
* double param_1 = obj->next(val);
*/
static_cast
- static_cast<바꾸려고 하는="" 타입="">(대상);
- static_cast<new_type<(expression)
- 실수와 정수, 열거형과 정수형, 실수와 실수 사이의 변환을 허용
Reference
https://leetcode.com/

Comments