2. Math Refresher Notes for Computer science.
02 May 2020 | Data structure_1
Introduction
- A quick refresher on some of the key math concepts we will see throughout the course.
Why is it Important?
- Computer science in its essence is applied mathematics. This means it has a strong foundation in many different types of math. Understanding the basics of some math functions will help to get a better picture of computer science as a whole
Lesson Notes
Logarithmic Functions
-
Log (short for logarithmic) functions are commonly referred to in computer science. This is because they are the inverse of exponential functions. Where an exponential function grows more and more over time, a log function grows less and less over time.
-
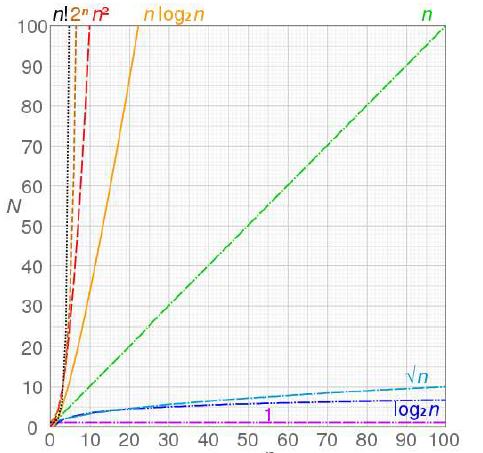
Below you can see the difference between these functions. On the bottom you will see a log(n), and then it’s inverse, near the top, the 2^n. Note how the log has a little two with it, this means it is using base two. Remember from the binary lesson, base 2 uses only 1 and 0. This is important when using with an online calculator. Make sure the log is set to base 2. Notice how the log function becomes almost horizontal, while the exponential function becomes almost vertical.
-
Let’s say for example this is a graph of run times. So the bottom is how many pieces of data are inserted, and the left is how long it will take. You will notice with a log function, we can insert 100 pieces of data and have a run-time below 5. With an exponential function however, we only have to insert around 5 pieces of data before our run-time exceeds 100.
-
Here is a good link that describes them in a slightly different way and has some practice examples. Understanding log functions in their entirety IS NOT required for this class. All you need to know is that they are efficient, and that they are the inverse of exponential functions.
Factorial Expressions
- Factorials are interesting expressions. The notation for them are n! . What this means is that we are going to multiply a series of numbers up until the variable n.
4! = 1 * 2 * 3 * 4 = 24
5! = 1 * 2 * 3 * 4 * 5 = 120
8! = 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 = 40,320
10! = 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 = 3,628,800
- As you can see, factorials grow at an astounding rate. If any of our functions ever reach this, they will most likely never finish. Almost, if not every algorithm in computer science can be accomplished in faster than n! time.
Algebraic Expressions
-
We will encounter a few algebraic expressions throughout the course. They may look something like nlogn or 2nlog(n^2) etc. All this means is that we have a variable n that will be plugged in to the equation. Because we don’t actually know how many pieces of data will go in to the algorithm, we use this n placeholder. (More about this in the next lecture).
-
Once we know the n value however, we can plug it in, and calculate the answer. For example, if n=32, we will then have nlogn or 32 * log(32). This would come out to 32 * 5 = 160 units of time.
Introduction
- A quick refresher on some of the key math concepts we will see throughout the course.
Why is it Important?
- Computer science in its essence is applied mathematics. This means it has a strong foundation in many different types of math. Understanding the basics of some math functions will help to get a better picture of computer science as a whole
Lesson Notes
Logarithmic Functions
-
Log (short for logarithmic) functions are commonly referred to in computer science. This is because they are the inverse of exponential functions. Where an exponential function grows more and more over time, a log function grows less and less over time.
-
Below you can see the difference between these functions. On the bottom you will see a log(n), and then it’s inverse, near the top, the 2^n. Note how the log has a little two with it, this means it is using base two. Remember from the binary lesson, base 2 uses only 1 and 0. This is important when using with an online calculator. Make sure the log is set to base 2. Notice how the log function becomes almost horizontal, while the exponential function becomes almost vertical.
-
Let’s say for example this is a graph of run times. So the bottom is how many pieces of data are inserted, and the left is how long it will take. You will notice with a log function, we can insert 100 pieces of data and have a run-time below 5. With an exponential function however, we only have to insert around 5 pieces of data before our run-time exceeds 100.
-
Here is a good link that describes them in a slightly different way and has some practice examples. Understanding log functions in their entirety IS NOT required for this class. All you need to know is that they are efficient, and that they are the inverse of exponential functions.
Factorial Expressions
- Factorials are interesting expressions. The notation for them are n! . What this means is that we are going to multiply a series of numbers up until the variable n.
4! = 1 * 2 * 3 * 4 = 24
5! = 1 * 2 * 3 * 4 * 5 = 120
8! = 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 = 40,320
10! = 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 = 3,628,800
- As you can see, factorials grow at an astounding rate. If any of our functions ever reach this, they will most likely never finish. Almost, if not every algorithm in computer science can be accomplished in faster than n! time.
Algebraic Expressions
-
We will encounter a few algebraic expressions throughout the course. They may look something like nlogn or 2nlog(n^2) etc. All this means is that we have a variable n that will be plugged in to the equation. Because we don’t actually know how many pieces of data will go in to the algorithm, we use this n placeholder. (More about this in the next lecture).
-
Once we know the n value however, we can plug it in, and calculate the answer. For example, if n=32, we will then have nlogn or 32 * log(32). This would come out to 32 * 5 = 160 units of time.

Comments