4. Fixed Array
04 May 2020 | Data structure_1
Introduction
- Arrays are a way of storing data in a linear sequence. This creates a fast-organized data structure
Why is it Important?
- Arrays are used everywhere. Because of their easy design and quick recall, they are widely used to store information during program execution. They can also be used to build more advanced data structures like stacks and queues.
Lesson Notes
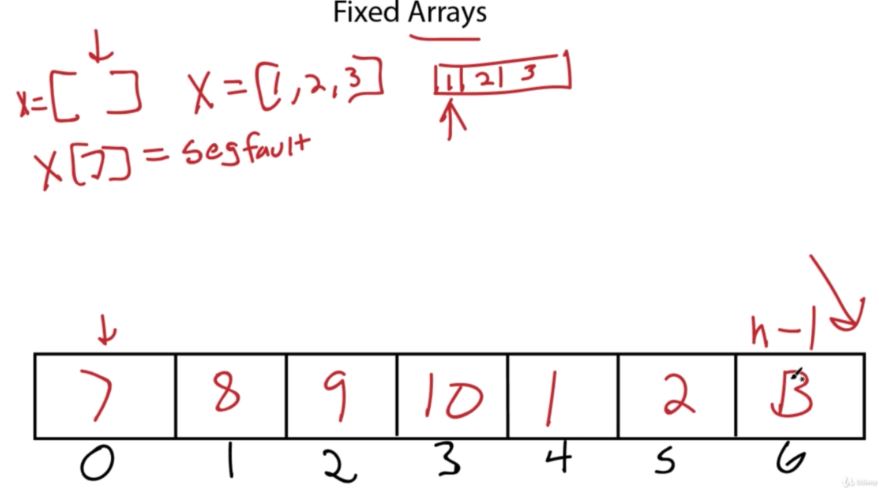
- Fixed arrays are the most basic version of an array. They are created with a fixed size and stick to this size throughout their execution
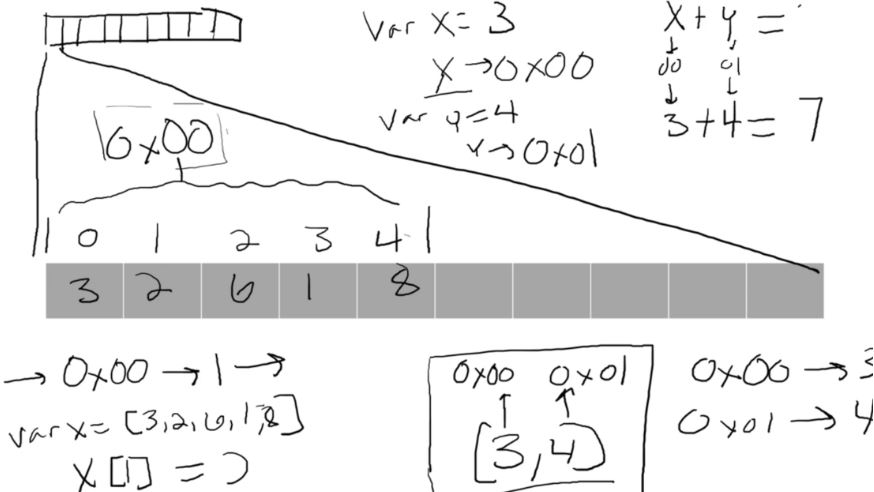
- Ox00 는 메모리 address 주소
-
정해진 어레이 크기에 넘어가는 수를 구하려고 하면, SegFault가 이러난다.
-
An array works by allocating a section of memory for storage. Then whenever we call the array, it returns the location of start of the array. We can then apply the appropriate index number to get to any point in that array instantly.
-
For example, in the figure above, the array myList is created and references the very beginning of the array. You can see this through the “reference” box that points to before the first element of the array.
-
We can then put a number in the [] after myList to get a specific element of the array. So if we put myList[5] we would get in return 34.33.
Run Times
-
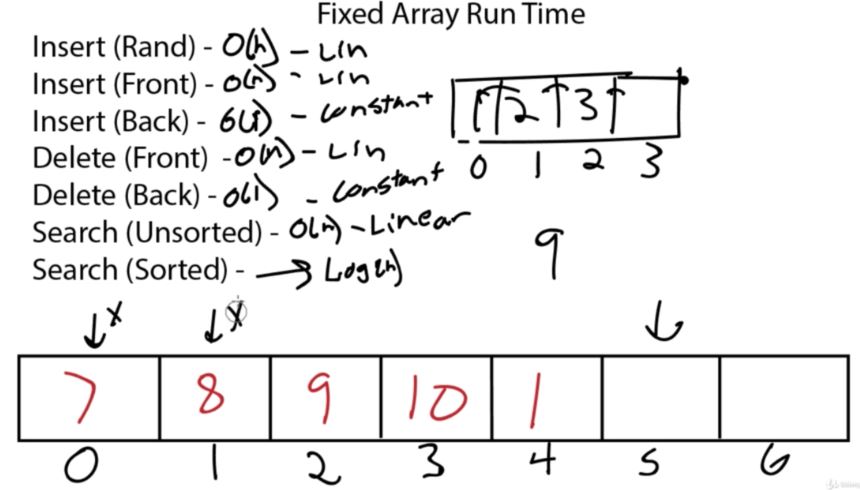
Insertion Random: O(n) – It’s easy to insert randomly anywhere in the array. Getting to the location of insertion take O(1) time. However, if you want to preserve order, there is a chance you will have to move O(n) elements to put the number there. Therefore, it’s O(n).
-
The reason we use n is because it will show us how our program might react differently to different amounts of data. We as computer scientists never know how many pieces of data our programs are going to handle. So instead, we look at how our program is going to grow with different amounts of inputs.
-
Insertion Front: O(n) – Inserting in the front of an array will usually take O(n) time, as you have to shift up to n elements backwards to insert properly.
-
Insertion Back: O(1) – Nothing has to be shifted, so you can accomplish this in O(1) time.
-
Deletion Random: O(n) – Deleting randomly from the array is just like inserting randomly. You can get to and remove the element in O(1) time. However, if you need to delete an element and not create a hole, then this becomes O(n) as you will need to shift everything to cover the hole.
-
Deletion Front: O(n) – Same as Insertion, a shift of up to n elements will be required.
-
Search Unsorted: O(n) – If the array is unsorted, there is no way of knowing where the element is going to be. So at worst case, it’s going to be a search of the entire array to find the element.
-
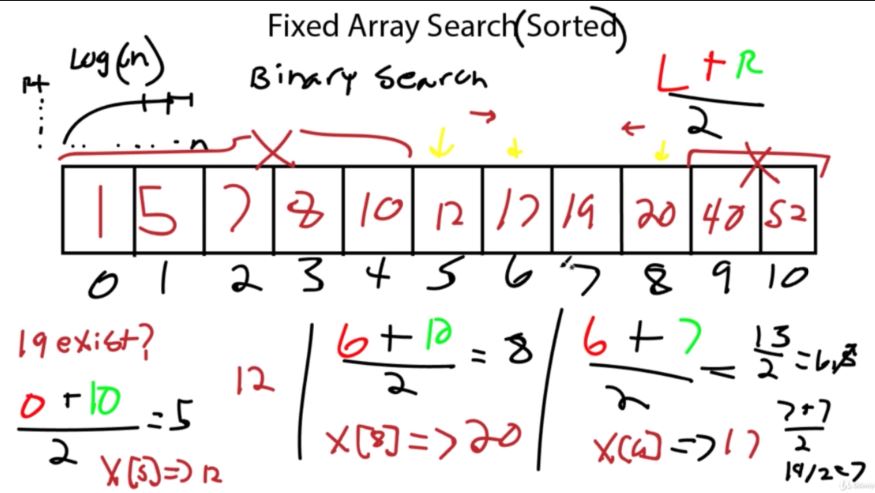
Search Sorted: O(logn) – If the array is sorted, we can keep cutting the array in half to find the element we are searching for. This means it will take at most logn operations to find our element. (Reverse exponential).
Introduction
- Arrays are a way of storing data in a linear sequence. This creates a fast-organized data structure
Why is it Important?
- Arrays are used everywhere. Because of their easy design and quick recall, they are widely used to store information during program execution. They can also be used to build more advanced data structures like stacks and queues.
Lesson Notes
- Fixed arrays are the most basic version of an array. They are created with a fixed size and stick to this size throughout their execution
- Ox00 는 메모리 address 주소
-
정해진 어레이 크기에 넘어가는 수를 구하려고 하면, SegFault가 이러난다.
-
An array works by allocating a section of memory for storage. Then whenever we call the array, it returns the location of start of the array. We can then apply the appropriate index number to get to any point in that array instantly.
-
For example, in the figure above, the array myList is created and references the very beginning of the array. You can see this through the “reference” box that points to before the first element of the array.
-
We can then put a number in the [] after myList to get a specific element of the array. So if we put myList[5] we would get in return 34.33.
Run Times
-
Insertion Random: O(n) – It’s easy to insert randomly anywhere in the array. Getting to the location of insertion take O(1) time. However, if you want to preserve order, there is a chance you will have to move O(n) elements to put the number there. Therefore, it’s O(n).
-
The reason we use n is because it will show us how our program might react differently to different amounts of data. We as computer scientists never know how many pieces of data our programs are going to handle. So instead, we look at how our program is going to grow with different amounts of inputs.
-
Insertion Front: O(n) – Inserting in the front of an array will usually take O(n) time, as you have to shift up to n elements backwards to insert properly.
-
Insertion Back: O(1) – Nothing has to be shifted, so you can accomplish this in O(1) time.
-
Deletion Random: O(n) – Deleting randomly from the array is just like inserting randomly. You can get to and remove the element in O(1) time. However, if you need to delete an element and not create a hole, then this becomes O(n) as you will need to shift everything to cover the hole.
-
Deletion Front: O(n) – Same as Insertion, a shift of up to n elements will be required.
-
Search Unsorted: O(n) – If the array is unsorted, there is no way of knowing where the element is going to be. So at worst case, it’s going to be a search of the entire array to find the element.
-
Search Sorted: O(logn) – If the array is sorted, we can keep cutting the array in half to find the element we are searching for. This means it will take at most logn operations to find our element. (Reverse exponential).


Comments