5. Circular and Dynamic Array
05 May 2020 | Data structure_1
Introduction
- Arrays can be improved from basic fixed sized arrays. These improvements can help make the arrays more flexible and efficient.
Why is it Important?
- Through these improvements we are able to dynamically store data, as well as decrease the insertion time and deletion times.
Lesson Notes
Circular Array
-
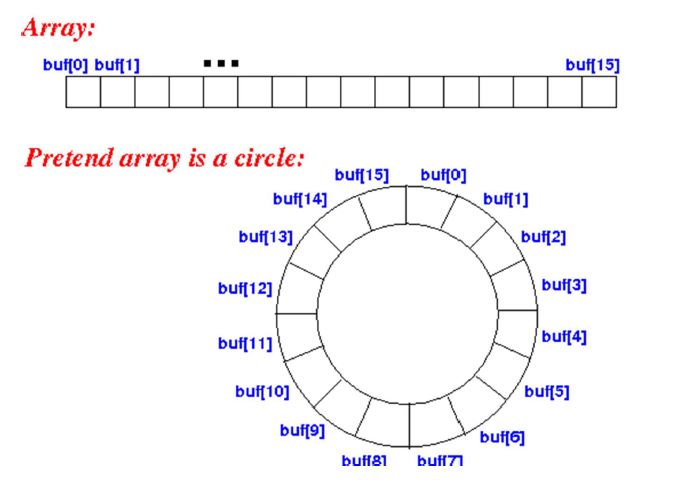
One of the major problems with a typical array is that we could reach O(n) whenever we tried inserting or deleting into the front. The entire array had to be shifted, causing a lot of data to be touched that didn’t really need to be touched
-
To improve this, we pretend that the array is circular. This makes it so we never need to shift data.
-
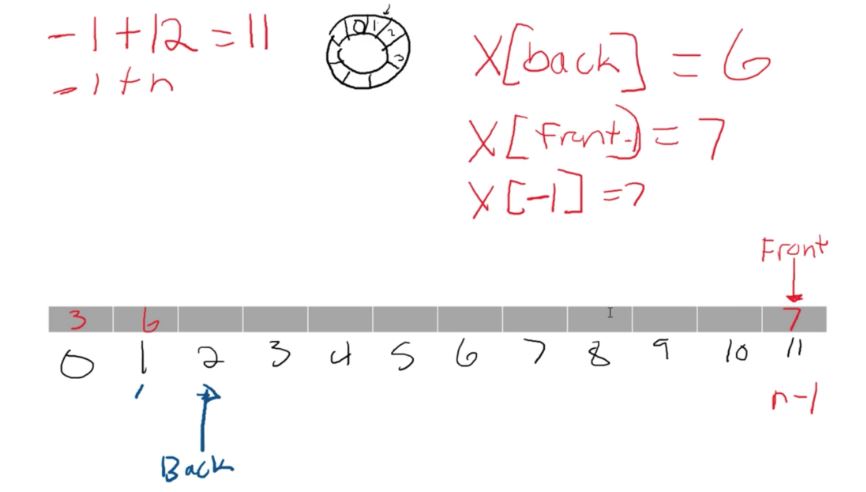
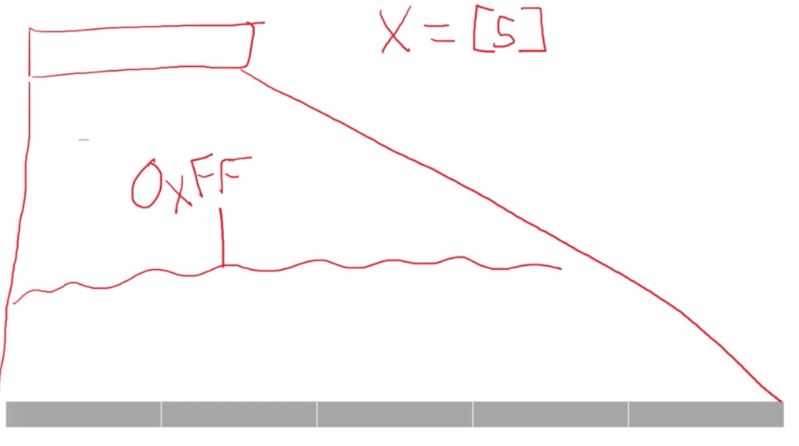
So how do we pretend it’s circular? We create two cursors. A “start” cursor, which points to the beginning of the array, and an “end” cursor which points to the end of the array. These cursors are then adjusted when an element is deleted or added
-
For example, let’s say we had some data in buff[0] that we wanted to delete. If we look at the typical horizontal array above, you will notice that when we delete this data, we will end up having to shift everything backwards to fill in the hole.
-
However, with the circular array, what we do is to move the “front” cursor to buff[1]. This makes buff[1] our new beginning of the array. We can now add or delete anything, and instead of moving the data, we just move the cursor around.
-
At some point the beginning of the array might be at buff[13] and the end might be at buff[6]. It just depends on how data is added and removed. Overall though, since we are only moving the location of the cursor, our run time improves to O(1) from O(n).
Dynamic Arrays
-
A dynamic array gives us the ability to expand our array whenever we run out of room. This means we don’t need to know how much data is being input beforehand, making it a lot more “real-world” friendly.
-
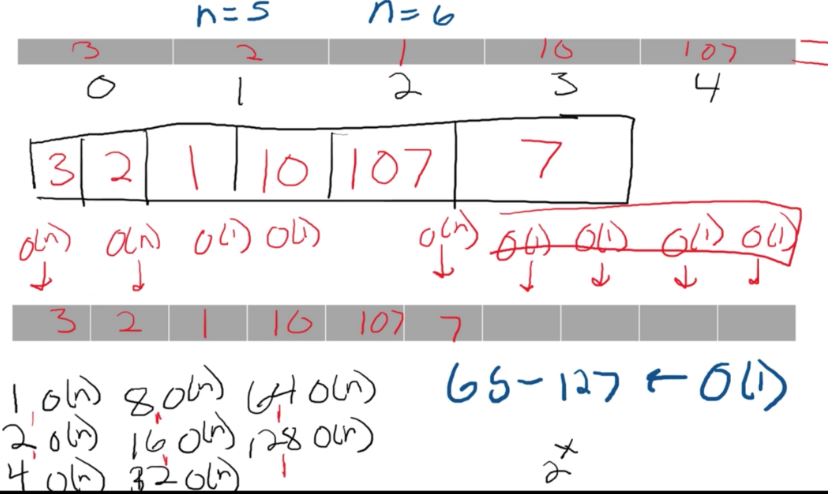
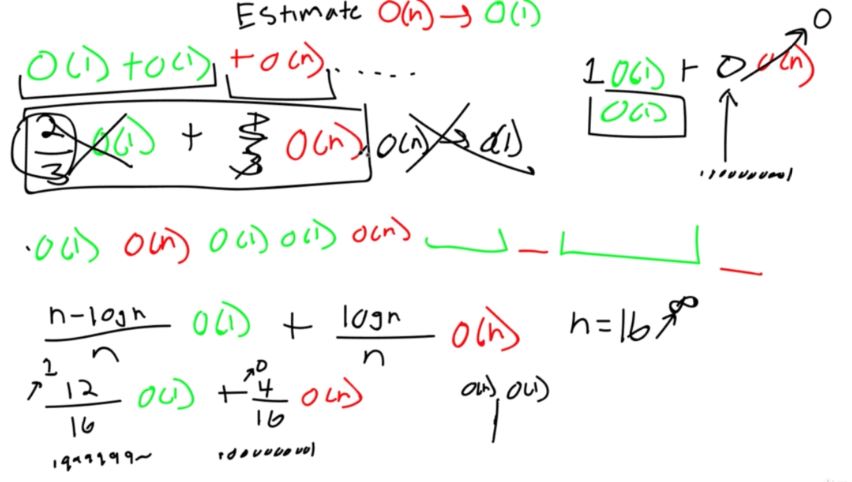
Expanding our array each time we run out of data however runs in O(n) time. This is because once an array is allocated, it can’t be expanded. So what we do is create a new array with a new size, and then transfer over all of the contents from the previous array.
-
This though requires we touch every single piece of data in the array, making the O(n) time. We can however improve this if we think about the problem a little bit further.
-
Instead of increasing the size of the array by 1 each time when we run out of data, we can instead double the size of the array.
-
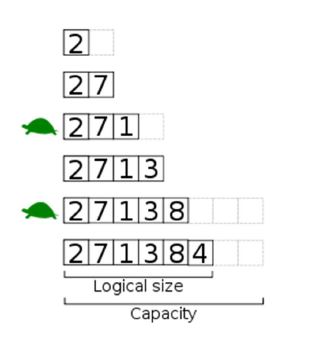
For this, we use the terms logical size, and physical size. The logical size is how many pieces of data are actually allocated in the array. The physical size is the size of the array itself. So what we want to do, is every time our logical size reaches our physical size, we want to double the physical size.
-
This doubling provides a less and less frequent use of the O(n) copying operation, which overall leads to something called an amortized O(1) relationship. Amortize here just means averaged. This means is that it is technically O(n) because of the copy operation, but when averaged out to infinity, it more closely resembles that of O(1). Because of this, we can say it’s basically O(1).
-
There is also a space-time complexity that needs to be thought of with this problem. The more you allocate after each “full” insert, the more chance there is of wasted space. It may speed up the run time, but may cost you a lot of storage space.
-
For example, let’s say you have an array with 65,536 slots that gets filled up. If we want to add another element to this, we will then have an array which is 131,072 elements big. That is a gigantic leap. So this is usually optimized depending on the program
-
This can all be expanded a bit farther. With some clever ingenuity(聪明才智), you can actually create a dynamic circular array, combining the best of everything mentioned.
-
This array would just be a dynamic array with front and end cursors. This would allow you to delete and add in constant time, and also to make sure that when the array runs out of room it wouldn’t take up much time either.
Array address
Quiz
Introduction
- Arrays can be improved from basic fixed sized arrays. These improvements can help make the arrays more flexible and efficient.
Why is it Important?
- Through these improvements we are able to dynamically store data, as well as decrease the insertion time and deletion times.
Lesson Notes
Circular Array
-
One of the major problems with a typical array is that we could reach O(n) whenever we tried inserting or deleting into the front. The entire array had to be shifted, causing a lot of data to be touched that didn’t really need to be touched
-
To improve this, we pretend that the array is circular. This makes it so we never need to shift data.
-
So how do we pretend it’s circular? We create two cursors. A “start” cursor, which points to the beginning of the array, and an “end” cursor which points to the end of the array. These cursors are then adjusted when an element is deleted or added
-
For example, let’s say we had some data in buff[0] that we wanted to delete. If we look at the typical horizontal array above, you will notice that when we delete this data, we will end up having to shift everything backwards to fill in the hole.
-
However, with the circular array, what we do is to move the “front” cursor to buff[1]. This makes buff[1] our new beginning of the array. We can now add or delete anything, and instead of moving the data, we just move the cursor around.
-
At some point the beginning of the array might be at buff[13] and the end might be at buff[6]. It just depends on how data is added and removed. Overall though, since we are only moving the location of the cursor, our run time improves to O(1) from O(n).
Dynamic Arrays
-
A dynamic array gives us the ability to expand our array whenever we run out of room. This means we don’t need to know how much data is being input beforehand, making it a lot more “real-world” friendly.
-
Expanding our array each time we run out of data however runs in O(n) time. This is because once an array is allocated, it can’t be expanded. So what we do is create a new array with a new size, and then transfer over all of the contents from the previous array.
-
This though requires we touch every single piece of data in the array, making the O(n) time. We can however improve this if we think about the problem a little bit further.
-
Instead of increasing the size of the array by 1 each time when we run out of data, we can instead double the size of the array.
-
For this, we use the terms logical size, and physical size. The logical size is how many pieces of data are actually allocated in the array. The physical size is the size of the array itself. So what we want to do, is every time our logical size reaches our physical size, we want to double the physical size.
-
This doubling provides a less and less frequent use of the O(n) copying operation, which overall leads to something called an amortized O(1) relationship. Amortize here just means averaged. This means is that it is technically O(n) because of the copy operation, but when averaged out to infinity, it more closely resembles that of O(1). Because of this, we can say it’s basically O(1).
-
There is also a space-time complexity that needs to be thought of with this problem. The more you allocate after each “full” insert, the more chance there is of wasted space. It may speed up the run time, but may cost you a lot of storage space.
-
For example, let’s say you have an array with 65,536 slots that gets filled up. If we want to add another element to this, we will then have an array which is 131,072 elements big. That is a gigantic leap. So this is usually optimized depending on the program
-
This can all be expanded a bit farther. With some clever ingenuity(聪明才智), you can actually create a dynamic circular array, combining the best of everything mentioned.
-
This array would just be a dynamic array with front and end cursors. This would allow you to delete and add in constant time, and also to make sure that when the array runs out of room it wouldn’t take up much time either.


Comments