6.sinlgy-Linked List
06 May 2020 | Data structure_1
Introduction
- Linked Lists are a core data structure that can link data together from multiple locations
Why is it Important?
- Linked Lists help us link data together from separate locations. In this way they are infinitely scalable and can contain multiple different types of data. This gives us a flexibility that arrays don’t give us.
Lesson Notes
Nodes
-
Nodes are the building blocks of Singly Linked Lists. They are a data structure which holds a few key pieces of information.
-
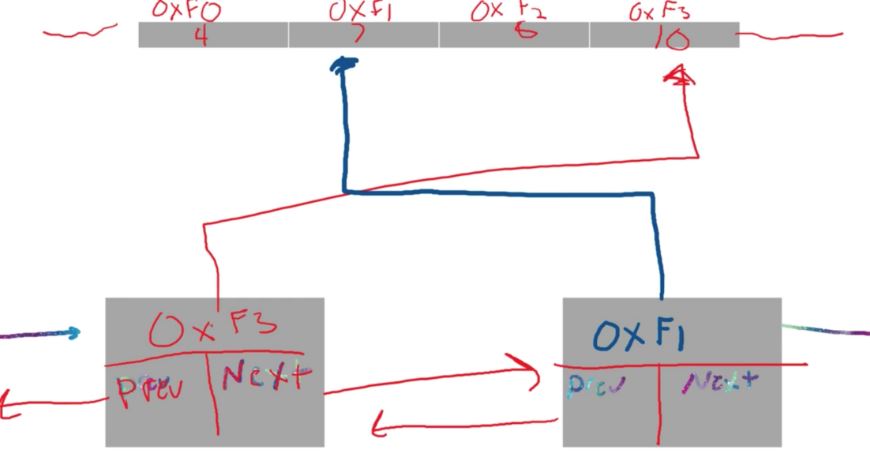
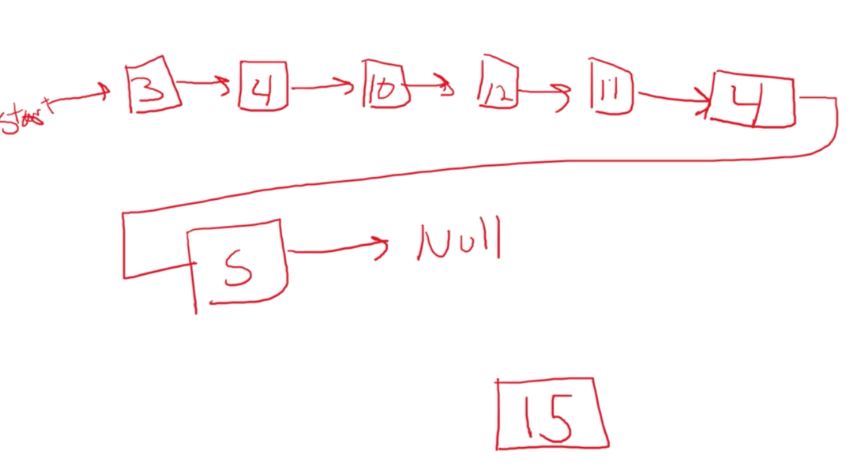
The node usually contains a piece of data (a number, letter, location, etc) and then pointers t other nodes. In a singly-linked list it contains a pointer to the next node in the array. If it is at the end of the array, then it just points to NULL, which means nothing.
Linked List
-
The very first node is designated as the “head” of the linked list. It is the node that is always pointed to when we call our linked list. This head is important, without it, we would lose our entire linked list.
-
An important difference between linked lists and arrays is that the data in the linked list aren’t directly accessible.
-
For example, if we had an array of tempArray = [H,E,A,P], we could access the P by calling tempArray[3]. This would instantly return us the P.
-
With a linked list however, we can’t do that. We only have the first node, and then where that node points to. This means that we have to traverse the entire list before we get to the P. So, if we want the P element, we will have to touch the H, E, and A before we get to it.
-
This means Linked Lists search times are typically slower than that of an array, even if the list is sorted, as there is no way to jump to a certain point.
Linked List Run Times
-
Insert(Rand): O(n) - To insert at a particular location, one has to traverse the list up to that point to insert there.
-
Insert(Front): O(1) – We just move the head pointer to the new node and point the new node at the old head.
-
Insert(Back): O(n) – We will have to traverse the entire array to get to the back. (We will find a way to improve this a little bit later)
-
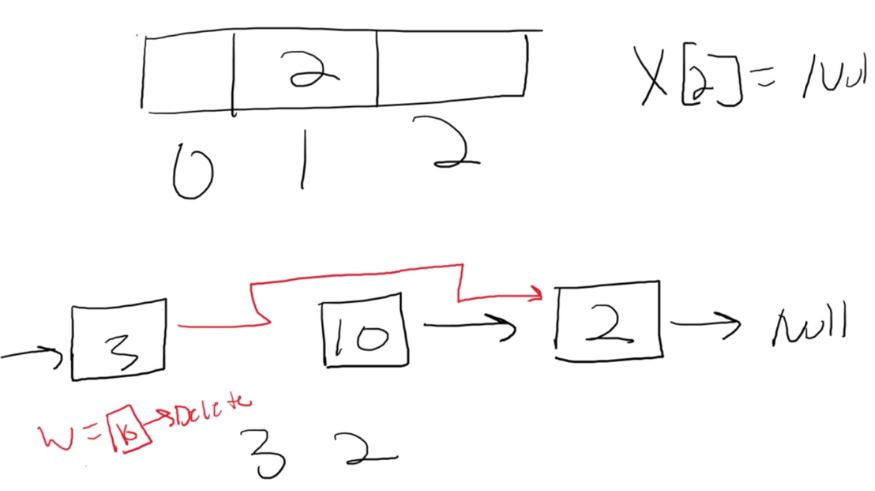
Delete(Random): O(n) – We must traverse the length of the element we want to delete
-
Delete(Front): O(1) – Just as easy as inserting, just have to remove the first element and repoint the head pointer
-
Search(Sorted): O(n) – Doesn’t matter if it’s sorted or not. We at worst have to traverse the entirety of the list to find the element. (And if the element isn’t in the list, we have to traverse the entire list to figure that out. )
-
Search(Unsorted): O(n) – Exactly the same as the Sorted.
Introduction
- Linked Lists are a core data structure that can link data together from multiple locations
Why is it Important?
- Linked Lists help us link data together from separate locations. In this way they are infinitely scalable and can contain multiple different types of data. This gives us a flexibility that arrays don’t give us.
Lesson Notes
Nodes
-
Nodes are the building blocks of Singly Linked Lists. They are a data structure which holds a few key pieces of information.
-
The node usually contains a piece of data (a number, letter, location, etc) and then pointers t other nodes. In a singly-linked list it contains a pointer to the next node in the array. If it is at the end of the array, then it just points to NULL, which means nothing.
Linked List
-
The very first node is designated as the “head” of the linked list. It is the node that is always pointed to when we call our linked list. This head is important, without it, we would lose our entire linked list.
-
An important difference between linked lists and arrays is that the data in the linked list aren’t directly accessible.
-
For example, if we had an array of tempArray = [H,E,A,P], we could access the P by calling tempArray[3]. This would instantly return us the P.
-
With a linked list however, we can’t do that. We only have the first node, and then where that node points to. This means that we have to traverse the entire list before we get to the P. So, if we want the P element, we will have to touch the H, E, and A before we get to it.
-
This means Linked Lists search times are typically slower than that of an array, even if the list is sorted, as there is no way to jump to a certain point.
Linked List Run Times
-
Insert(Rand): O(n) - To insert at a particular location, one has to traverse the list up to that point to insert there.
-
Insert(Front): O(1) – We just move the head pointer to the new node and point the new node at the old head.
-
Insert(Back): O(n) – We will have to traverse the entire array to get to the back. (We will find a way to improve this a little bit later)
-
Delete(Random): O(n) – We must traverse the length of the element we want to delete
-
Delete(Front): O(1) – Just as easy as inserting, just have to remove the first element and repoint the head pointer
-
Search(Sorted): O(n) – Doesn’t matter if it’s sorted or not. We at worst have to traverse the entirety of the list to find the element. (And if the element isn’t in the list, we have to traverse the entire list to figure that out. )
-
Search(Unsorted): O(n) – Exactly the same as the Sorted.


Comments