7. Doubly-Linked List
07 May 2020 | Data structure_1
Introduction
- We can improve linked lists by making them doubly-linked as well as creating a tail pointer.
Why is it Important?
- Giving us the ability to go forward AND backwards can be very helpful in a linked list. Also having the ability to start from the back can not only speed up access time, but it can make insertions to the back constant time.
Lesson Notes
Doubly-Linked List
-
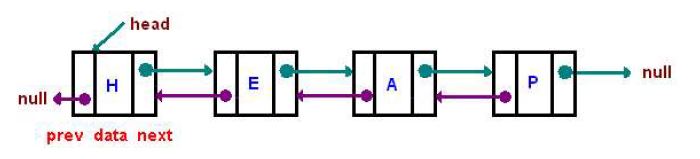
A doubly-linked list is the same as a singly-linked list with one major difference, instead of just a “next” pointer within each node, there is also a “previous” pointer. Note, this will typically increase the memory needed for the list, as each node now has another pointer to keep track of.
-
This however allows one to not only go forwards in the list, but also to go backwards in the list. This can be helpful for a large amount of applications.
-
For example, let’s say we want to print out the list back to front. With a singly-linked list, we would need to go to the last element, and print it. We would then have to start back at the beginning, go to n-1, then to n-2, and so on. We would have to keep restarting from the beginning.
-
So if we had the H->E->A->P example. If we wanted to print PEAH, we would have to first access H->E->A to get to P. We would then have to access H->E to get to the A and so on. This would make it so we would have to touch 10 pieces of data just to print out 5 pieces. This would scale up as well. If the array was 5 large, it would require 15 touches, 6 would require 21, and 7 would require 28.
-
The formula for this is actually known as a linear summation, or n(n+1) / 2, where n is the size of the list. So with our H->E->A->P example, it would be n=4, or 4(4+1) / 2 => 4(5)/2 => 20/2 => 10.
-
If we multiply the n through, we get (n^2 + n) / 2, which you guessed it, shows us it’s an n^2 formula.
-
If the list was doubly-linked however, we could go to the end of the list, print and move backwards until we get back to the front.
-
This means this particular operation will be reduced from O(n^2) to O(n), quite a change
Tail Pointer
-
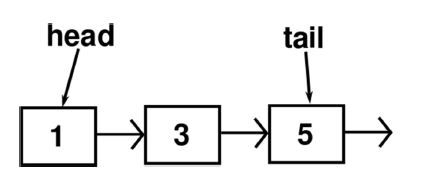
A tail pointer is a small addition that can improve the deletion and insertion to the back of the list. By default, we have a “head” pointer. This, as seen in the picture above, points to the beginning of a list. It is used to give us a node to start our traversals from. Without it, we would have no way of getting to the beginning of the list, and therefore the list would be lost in memory.
-
We however can also create another pointer, a “tail” pointer. This will point directly to the very last node added to the list.
-
How does this help us? Well think of the two cases in which we want to delete or add information to the back of the list. Without a tail pointer we have to traverse the entire list until we get to the end, which by default is an O(n) operation
-
So in the previous example H<->E<->A<->P (<-> signifies doubly-linked). Even with it being doubly-linked, it would still take O(n) operation to get to the back, and then O(n) operation to print from back to front. This would create O(2n) as the final run time. (This is simplified down to O(n) sure, but efficiency does matter at some point
-
With a tail pointer however, we can just start directly on the end, and then add or delete from there. This takes the O(n) operation and brings it back to O(1). So now our print back to front will require a O(1) + O(n) operation, which is just a natural O(n) timing.
-
Insert (Back): O(n) -> O(1)
-
Delete (Back): O(n) -> O(1)
-
So with two small additions, we have taken an operation that would have been O(n^2), and reduced it down to an actual O(n) timing. This is what computer science is all about. Coming up with solutions to help make programs more efficient.
Introduction
- We can improve linked lists by making them doubly-linked as well as creating a tail pointer.
Why is it Important?
- Giving us the ability to go forward AND backwards can be very helpful in a linked list. Also having the ability to start from the back can not only speed up access time, but it can make insertions to the back constant time.
Lesson Notes
Doubly-Linked List
-
A doubly-linked list is the same as a singly-linked list with one major difference, instead of just a “next” pointer within each node, there is also a “previous” pointer. Note, this will typically increase the memory needed for the list, as each node now has another pointer to keep track of.
-
This however allows one to not only go forwards in the list, but also to go backwards in the list. This can be helpful for a large amount of applications.
-
For example, let’s say we want to print out the list back to front. With a singly-linked list, we would need to go to the last element, and print it. We would then have to start back at the beginning, go to n-1, then to n-2, and so on. We would have to keep restarting from the beginning.
-
So if we had the H->E->A->P example. If we wanted to print PEAH, we would have to first access H->E->A to get to P. We would then have to access H->E to get to the A and so on. This would make it so we would have to touch 10 pieces of data just to print out 5 pieces. This would scale up as well. If the array was 5 large, it would require 15 touches, 6 would require 21, and 7 would require 28.
-
The formula for this is actually known as a linear summation, or n(n+1) / 2, where n is the size of the list. So with our H->E->A->P example, it would be n=4, or 4(4+1) / 2 => 4(5)/2 => 20/2 => 10.
-
If we multiply the n through, we get (n^2 + n) / 2, which you guessed it, shows us it’s an n^2 formula.
-
If the list was doubly-linked however, we could go to the end of the list, print and move backwards until we get back to the front.
-
This means this particular operation will be reduced from O(n^2) to O(n), quite a change
Tail Pointer
-
A tail pointer is a small addition that can improve the deletion and insertion to the back of the list. By default, we have a “head” pointer. This, as seen in the picture above, points to the beginning of a list. It is used to give us a node to start our traversals from. Without it, we would have no way of getting to the beginning of the list, and therefore the list would be lost in memory.
-
We however can also create another pointer, a “tail” pointer. This will point directly to the very last node added to the list.
-
How does this help us? Well think of the two cases in which we want to delete or add information to the back of the list. Without a tail pointer we have to traverse the entire list until we get to the end, which by default is an O(n) operation
-
So in the previous example H<->E<->A<->P (<-> signifies doubly-linked). Even with it being doubly-linked, it would still take O(n) operation to get to the back, and then O(n) operation to print from back to front. This would create O(2n) as the final run time. (This is simplified down to O(n) sure, but efficiency does matter at some point
-
With a tail pointer however, we can just start directly on the end, and then add or delete from there. This takes the O(n) operation and brings it back to O(1). So now our print back to front will require a O(1) + O(n) operation, which is just a natural O(n) timing.
-
Insert (Back): O(n) -> O(1)
-
Delete (Back): O(n) -> O(1)
-
So with two small additions, we have taken an operation that would have been O(n^2), and reduced it down to an actual O(n) timing. This is what computer science is all about. Coming up with solutions to help make programs more efficient.

Comments