13. Quick sort
13 May 2020 | Data structure_1
Introduction
- Quick Sort is our first “fast” sorting algorithm. It divides the data cleverly to reduce the run time of the algorithm.
Why is it Important?
- Quick sort is the next step in sorting algorithms. This sorting algorithm uses a smart way to divide the data so that it can reduce the run time. This comes at the cost of added complexity
Lesson Notes
-
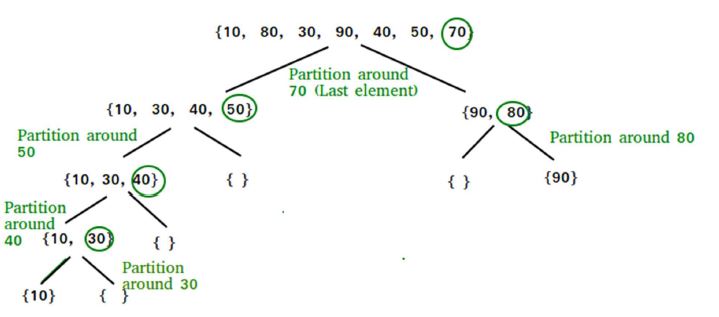
Quick Sort works off picking a “pivot” point. All numbers less than the pivot point go to the left, and all numbers greater than the pivot point go to the right. It then reapplies this algorithm to each side of the pivot.
-
This creates an algorithm which implements a divide and conquer approach to sorting. Because of it’s ability to split up the sorting, it is able to sort in a log(n) like manner.
-
As you can see, as the algorithm splits itself with every step, it is slowly creating a sorted algorithm. No longer does it need to run through the array for each number to be sorted. Now it can just keep breaking up the numbers until they are all sorted.
-
If we look at the example above, we can read it from left to right and have a sorted array. We have {10,30,40,50,70,80,90} Each level of this algorithm takes n amount of time. Because of the way we split up the information however, there will only be log(n) levels. This means the general run time of the algorithm is going to be the number of levels multiplied by n, or nlogn, a strong improvement on the n^2 we have been seeing
-
With this algorithm however, the pivot point is important. If we keep picking pivot points that don’t split up the data, then we will not divide the data correctly. Instead of log(n) levels, we have the possibility of getting n levels. This means it will come out to n X n again, getting us the n^2 time
-
Best Time: Ω(nlogn) : The best case in this scenario is if we pick a perfect pivot point to split the data. It doesn’t matter if the array comes in sorted or not. The pivot point is what matters the most. If we pick a pivot point that perfectly splits the data each time, then we will have log(n) levels, and therefore the nlogn run time
-
Average Time: Θ(nlogn) : The average time happens when we choose a decent pivot point. As long as we can split up the data and let the program divide and conquer, we get an nlogn time.
-
Worst Time: O(n^2) : The worst-case scenario happens when we choose a bad pivot point. Instead of dividing the work up to log(n), we keep only splitting out 1 number each time. (The number is larger or smaller than the rest of the array). This makes it so we have roughly n levels. Therefore we end up having the n X n relationship, instead of the n X logn relationship.
Comparison
Quiz
Introduction
- Quick Sort is our first “fast” sorting algorithm. It divides the data cleverly to reduce the run time of the algorithm.
Why is it Important?
- Quick sort is the next step in sorting algorithms. This sorting algorithm uses a smart way to divide the data so that it can reduce the run time. This comes at the cost of added complexity
Lesson Notes
-
Quick Sort works off picking a “pivot” point. All numbers less than the pivot point go to the left, and all numbers greater than the pivot point go to the right. It then reapplies this algorithm to each side of the pivot.
-
This creates an algorithm which implements a divide and conquer approach to sorting. Because of it’s ability to split up the sorting, it is able to sort in a log(n) like manner.
-
As you can see, as the algorithm splits itself with every step, it is slowly creating a sorted algorithm. No longer does it need to run through the array for each number to be sorted. Now it can just keep breaking up the numbers until they are all sorted.
-
If we look at the example above, we can read it from left to right and have a sorted array. We have {10,30,40,50,70,80,90} Each level of this algorithm takes n amount of time. Because of the way we split up the information however, there will only be log(n) levels. This means the general run time of the algorithm is going to be the number of levels multiplied by n, or nlogn, a strong improvement on the n^2 we have been seeing
-
With this algorithm however, the pivot point is important. If we keep picking pivot points that don’t split up the data, then we will not divide the data correctly. Instead of log(n) levels, we have the possibility of getting n levels. This means it will come out to n X n again, getting us the n^2 time
-
Best Time: Ω(nlogn) : The best case in this scenario is if we pick a perfect pivot point to split the data. It doesn’t matter if the array comes in sorted or not. The pivot point is what matters the most. If we pick a pivot point that perfectly splits the data each time, then we will have log(n) levels, and therefore the nlogn run time
-
Average Time: Θ(nlogn) : The average time happens when we choose a decent pivot point. As long as we can split up the data and let the program divide and conquer, we get an nlogn time.
-
Worst Time: O(n^2) : The worst-case scenario happens when we choose a bad pivot point. Instead of dividing the work up to log(n), we keep only splitting out 1 number each time. (The number is larger or smaller than the rest of the array). This makes it so we have roughly n levels. Therefore we end up having the n X n relationship, instead of the n X logn relationship.




Comments