17. Heap Notes
17 May 2020 | Data structure_1
Introduction
- Heaps are a subdivision of Trees with a few rules. These rules, just like with Stacks and Queues, give these data structures many essential roles.
Why is it Important?
- Heaps are used for a variety of applications. They can act as priority queues, help with graph traversals, and provide a data structure that makes finding the extreme value O(1) time
Lesson Notes
-
Heaps in essence are just stricter trees. They have all the same properties of trees, with the additional “Heap Property” rule added.
-
The heap property is a rule which gives a relationship between the parent and child nodes within a tree. It states that the parent node must always be either greater, or less than its children. If it has to be greater, then it is a max heap, if less, a min heap.
-
This property propagates throughout the tree. Since every parent has to be greater or less than, the root, or the top of the tree, must be the greatest/least
-
The simplest heap is the binary heap. This is a heap in which each node of the heap has only two children and must maintain a complete tree pattern
-
A complete tree is a tree which every level, expect the last, is filled, and all nodes are as far left as possible.
- This is an example of a complete tree. Notice how it’s completely filled, and the last level fills from left to right.
-
This is an example of a tree which isn’t complete. The F should be shifted as a left child of C to make this complete
-
Due to the structure of a heap, most of the run times are logn, as it only takes the height of the tree to get to any given node. We have previously learned that trees are built in a structure that lends this height to be equal to logn time.
Run time
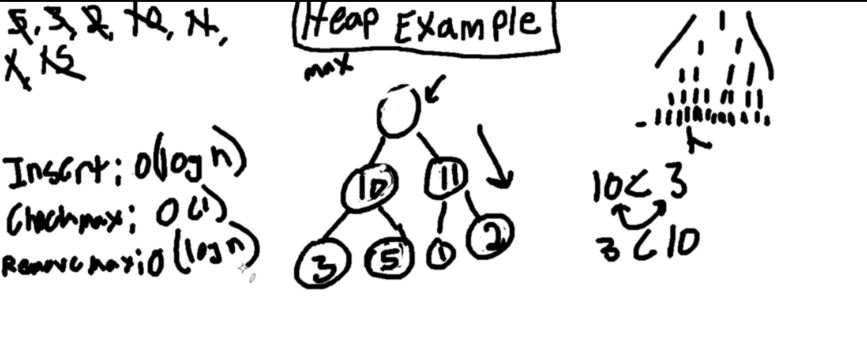
- Insert: O(logn)
- Delete: O(logn)
- GetMin: O(1)
Heap Example
Applications
- Heaps are great for priority queues, as the most “important” task will always be at the top, and really fast to retrieve. They are also used in more complex algorithms like Dijkstra’s Shortest Path Algorithm.
Introduction
- Heaps are a subdivision of Trees with a few rules. These rules, just like with Stacks and Queues, give these data structures many essential roles.
Why is it Important?
- Heaps are used for a variety of applications. They can act as priority queues, help with graph traversals, and provide a data structure that makes finding the extreme value O(1) time
Lesson Notes
-
Heaps in essence are just stricter trees. They have all the same properties of trees, with the additional “Heap Property” rule added.
-
The heap property is a rule which gives a relationship between the parent and child nodes within a tree. It states that the parent node must always be either greater, or less than its children. If it has to be greater, then it is a max heap, if less, a min heap.
-
This property propagates throughout the tree. Since every parent has to be greater or less than, the root, or the top of the tree, must be the greatest/least
-
The simplest heap is the binary heap. This is a heap in which each node of the heap has only two children and must maintain a complete tree pattern
-
A complete tree is a tree which every level, expect the last, is filled, and all nodes are as far left as possible.
- This is an example of a complete tree. Notice how it’s completely filled, and the last level fills from left to right.
-
This is an example of a tree which isn’t complete. The F should be shifted as a left child of C to make this complete
-
Due to the structure of a heap, most of the run times are logn, as it only takes the height of the tree to get to any given node. We have previously learned that trees are built in a structure that lends this height to be equal to logn time.
Run time
- Insert: O(logn)
- Delete: O(logn)
- GetMin: O(1)
Heap Example
Applications
- Heaps are great for priority queues, as the most “important” task will always be at the top, and really fast to retrieve. They are also used in more complex algorithms like Dijkstra’s Shortest Path Algorithm.







Comments