HomoGraphy(perspective Transform, Bird Eyes View)
13 Feb 2022 | Machine Vision
Homo에 대한 이해
Homo 즉, 선형성을 가졌다라고 이해하면된다. 선형성을 가졌다는 unique solution이 있고 Singularity가 아니기 때문에 우리가 풀고자하는 문제들에 주어진 value와 미지수에 관한 관계식을 구할 수 있고, 표현할 수있는 사람이 문제를 풀 수 있다라는 뜻이다.
HomoGraphy
In the field of computer vision, any two images of the same planar surface in space are related by a homography(单应性).
즉, homography를 통해서 Perspective transformation(Bird Eyes View 처럼 이미지를 눞혀서 보고)이 가능하고 파라노마 처럼 이미지를 스티칭 할 수 있다.
This has many practical applications.
예시로,
homography 를 적용하지 않는다면 어떻게 될까? 원근법으로 인해 빨간색칸의 pixel 기울기 값은 정말 클 것이고 그에 반에 멀리있는 파란색칸의 pixel 기울기의 변화량은 미미할 것이다.
homography를 쓴다면 상응하는 피처에 대해 원근법을 표현할 수 있다.
Visual SLAM에서는
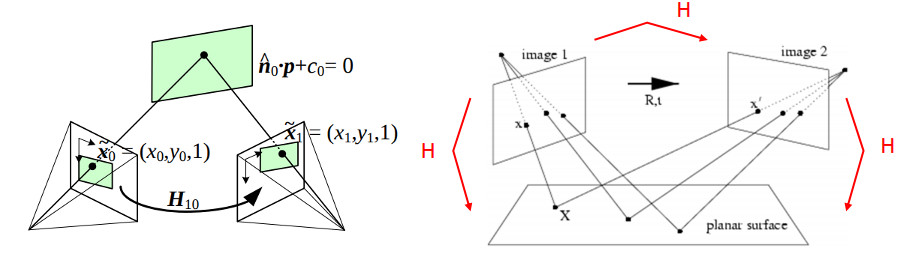
카메라 A와 B에서 바라보는 물체의 상의점 p에 대해서, A에서 p를 바라보는 것을 카메라 좌표 X1, B에서 p를 바라보는 것은 카메라 좌표 X2라고 할때, 두 카메라간에 선형관계(Transformation Matrix)가 HomoGraphy를 통해 homogeneous coordinate상으로 표혐 및 매칭을 시킬 수 있다.
REFERENCE
Homo에 대한 이해
Homo 즉, 선형성을 가졌다라고 이해하면된다. 선형성을 가졌다는 unique solution이 있고 Singularity가 아니기 때문에 우리가 풀고자하는 문제들에 주어진 value와 미지수에 관한 관계식을 구할 수 있고, 표현할 수있는 사람이 문제를 풀 수 있다라는 뜻이다.
HomoGraphy
In the field of computer vision, any two images of the same planar surface in space are related by a homography(单应性).
즉, homography를 통해서 Perspective transformation(Bird Eyes View 처럼 이미지를 눞혀서 보고)이 가능하고 파라노마 처럼 이미지를 스티칭 할 수 있다.
This has many practical applications.
예시로,
homography 를 적용하지 않는다면 어떻게 될까? 원근법으로 인해 빨간색칸의 pixel 기울기 값은 정말 클 것이고 그에 반에 멀리있는 파란색칸의 pixel 기울기의 변화량은 미미할 것이다.
homography를 쓴다면 상응하는 피처에 대해 원근법을 표현할 수 있다.
Visual SLAM에서는
카메라 A와 B에서 바라보는 물체의 상의점 p에 대해서, A에서 p를 바라보는 것을 카메라 좌표 X1, B에서 p를 바라보는 것은 카메라 좌표 X2라고 할때, 두 카메라간에 선형관계(Transformation Matrix)가 HomoGraphy를 통해 homogeneous coordinate상으로 표혐 및 매칭을 시킬 수 있다.



Comments