1.Introduction to Optimization
01 Oct 2019 | Optimization method
1. Introduction
what is optimization?
- An important tool in daily life, business and engineer
- Running a business: to maximize profit, minimize loss, maximize efficiency, or minimize risk.
- Design: minimize the weight of a bridge, and maximize the strength, within the design constrains; airplane engineering such as shape design and material selection, packing transistors in a computer chip in a functional way.
- Planning: select a flight route to minimize time or fuel consumption of an airplane
- Supermarket pricing and logistic
- Big data/AI
- Formal definition: to minimize (or maximize) a real function by deciding the values of free variables from within an allowed set.
Classification of optimization problems
- Continuous vs Discrete
- Constrained vs Unconstrained
- Global vs Local
- Stochastic vs Deterministic
- Convex vs Nonconvex
- Stochastic : random variable(DSPG)
- Convex has a lot of problem come in
- Convex form in range
- λ ∈ {0,1} (0~1)
Mathematical optimization
- optimal solution $x^*$ has smallest value of $f_0$ among all vectors that satisfy the constraints
Examples
- portfolio optimization
- variables: amounts invested in different assets
- constraints: budget, max./min. investment per asset, minimum return
- max/min : minimum could be zero, so we’re not allowed to actually purchase
- minimum return: we expect from this collection from this portfolio
- objective: overall risk or return variance
- ex) 500 stocks in can invest in, in my mean return absolutely muse excess 11% period
- device sizing in electronic circuits
- variables: device widths and lengths
- constraints: manufacturing limits, timing requirements, maximum area
- objective: power consumption
- data fitting
- variables: model parameters
- constraints: prior information, parameter limits
- objective: measure of misfit or prediction error
Examples
Examples
- Find two nonnegative numbers whose sum is up to 6 so that their product is a maximum.
- It is equivalent to find the largest area of a rectangular region provided that its perimeter is no greater than 12.
- Problem: let the two numbers be x, y, solve
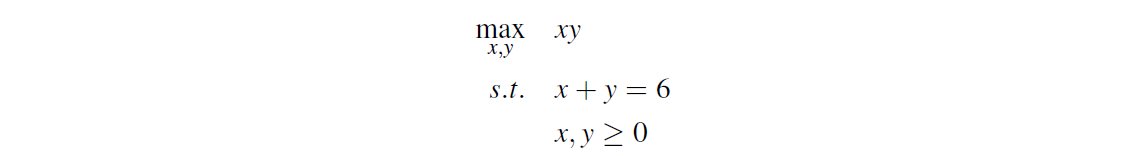
Examples
- Find a line that “best” fit three given points (x1, y1) = (2, 1), (x2, y2) = (3, 6) and (x3, y3) = (5, 4).
- Problem: let the line equation be y = ax + b, in the following least square sense:
Traveling sales man problem (TSMP)
- A salesman needs to visit a number (n) of cities, denoted by city 1, 2, · · · , n.
- The distances between cities are known, i.e. d_ij denotes the distance between city i and city j.
- The salesman wants to travel each city once in turn and in the meantime minimize the total travel distance.
- What order should be used?
- Problem: denote the order of travelling by ($i_1$, · · · , $i_n$), model
- this is polynomial time
Solving optimization problems
- general optimization problem (find a point: global optimization)
- very difficult to solve
- methods involve some compromise, e.g., very long computation time, or not always finding the solution
- exceptions : certain problem classes can be solved efficiently and reliably (Global solution)
- least-squares problems (we get the answer in period)
- linear programming problems (we get the answer in period)
- convex optimization problems (Global solution)
- most problem can not be optimized, but we use convex optimization solve the problem
- ex) singular values, principal component analysis
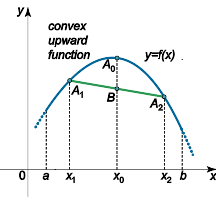
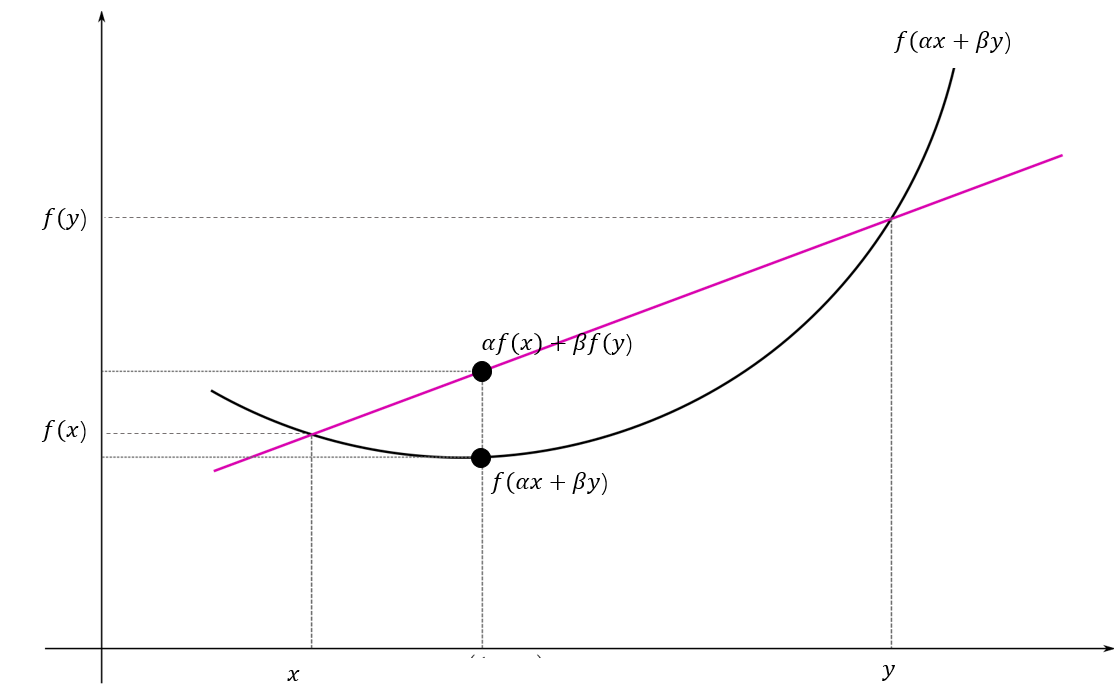
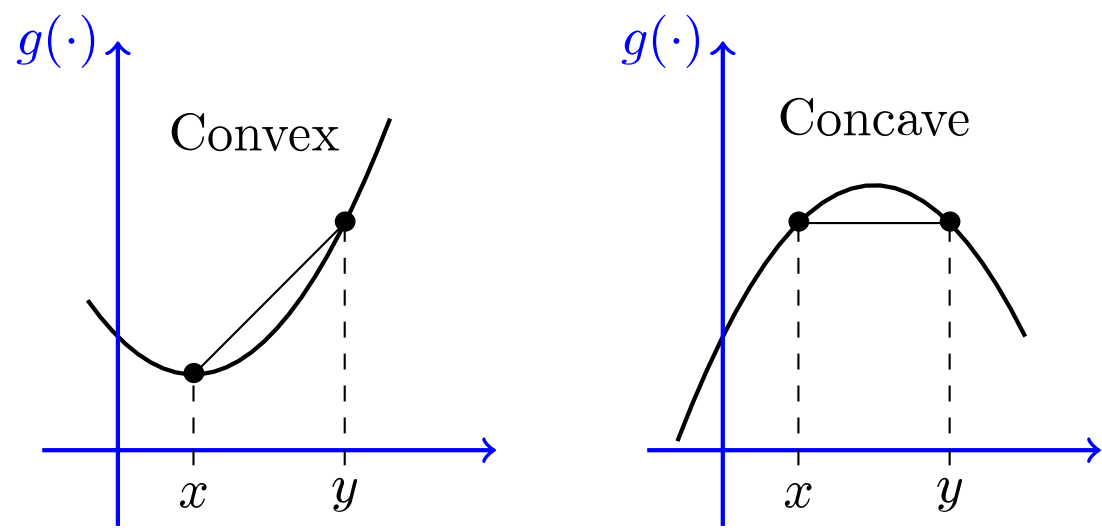
Convex optimization problem
- objective and constraint functions are convex:
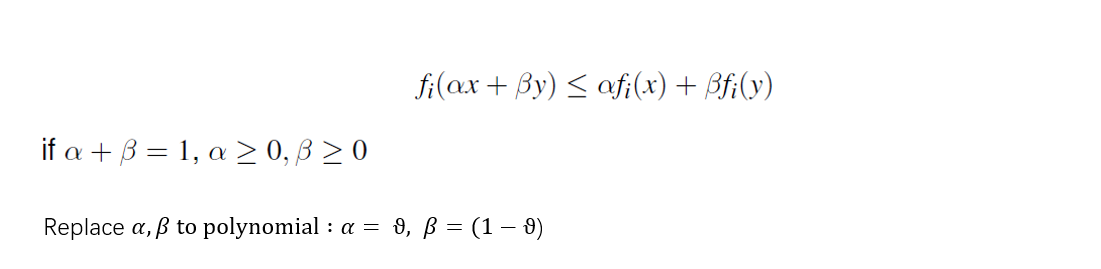
- includes least-squares problems and linear programs as special cases
- linear function are right on the boundary they have zero curvature(弯曲)
- so one way to say convex is just positive curvature(can solve problem)
Convex optimization problem
Convex optimization problem
- solving convex optimization problems
- no analytical solution
- reliable and efficient algorithms
- computation time (roughly) proportional to max{n3, n2m, F}, where F is cost of evaluating $f_i$’s and their first and second derivatives(this is basically square)
- almost a technology
- using convex optimization
Convex optimization example
- I have surface here with patches and I have some lamps here and we are going to choose the illumination powers in the lamps. that’s our variable. we’ll say the illumination on a patch here is going to be a sum of illumination from the lamps and it is going to be following proportional to the lamp power. and proportionality constant can be an inverse square law. R is the distance between patch and lamp, and there will be something which is a shading effect because obviously if we are coming in straight on. we get full power if this lamp for examples, put little illumination on here and if this were below it’s horizon if there were a lamp here, it would be not illuminate this patch at all
Least squares problems
Variants of Least squares
Linear Programming
- huge amount of qualitative intelligent things about linear program what we can not do is we can not write down formula for solution

- solving linear programs
- no analytical formula for solution ( there is no formula, there is no a transpose A inverse a transpose B)
- reliable and efficient algorithms and software
- computation time proportional to $n^2$m if m >= n; less with structure (same as least square)
- m : number of contain
- a mature technology
- a few standard tricks used to convert problems into linear programs
- e.g., problems involving $l_1$- or $l_∞$- norms, piecewise(分段)-linear functions
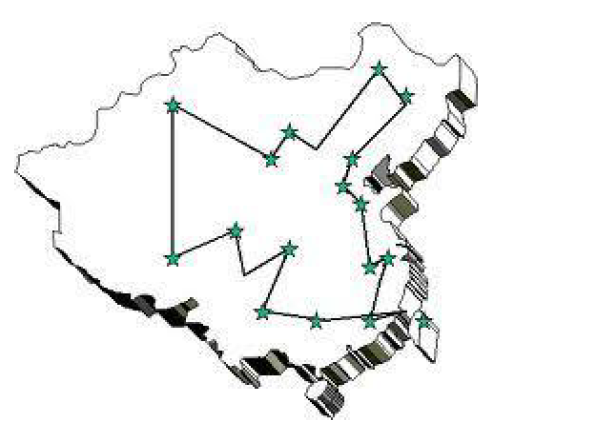
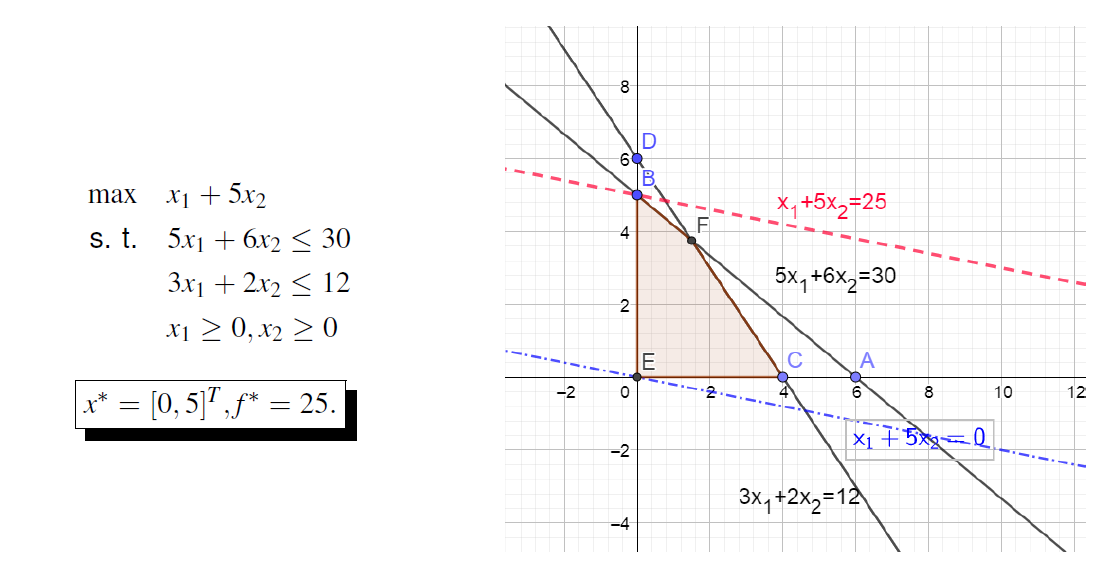
Graphic optimization in 2D
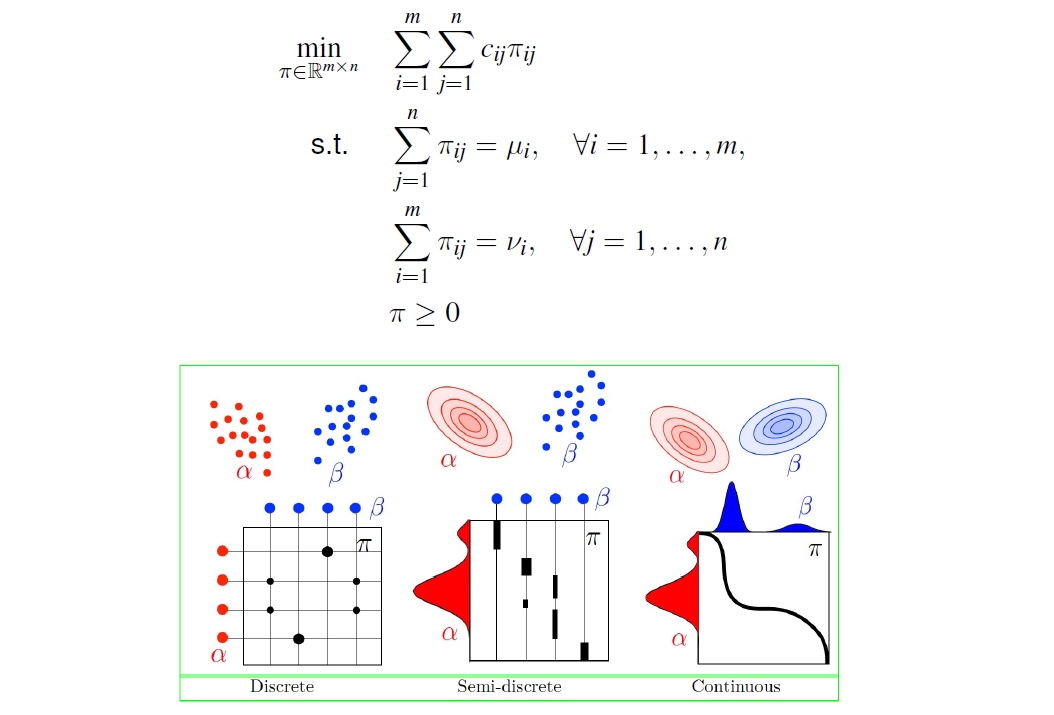
Example: The transportation problem
Optimal transport
Optimal transport: LP
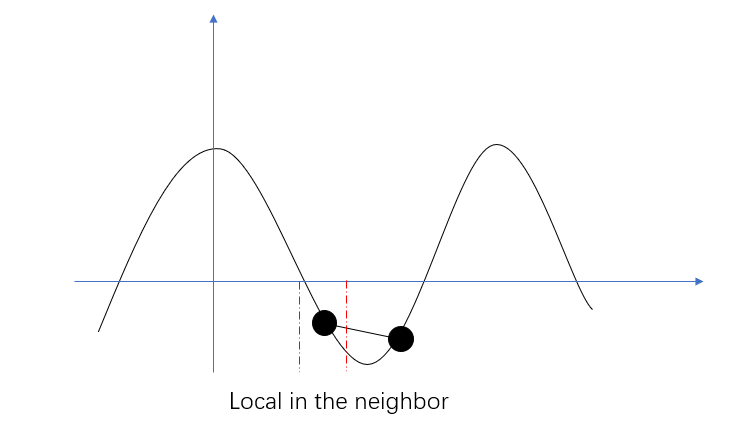
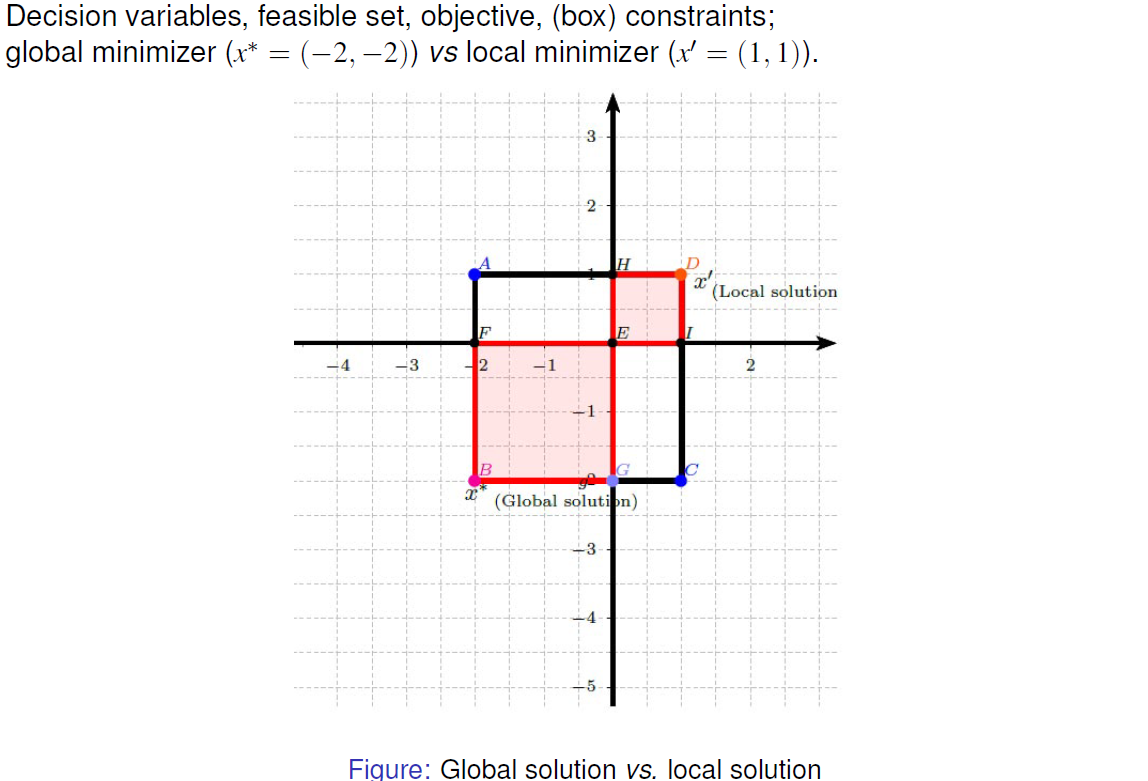
Global vs local solution
Global vs local solution
Graph
Reference
1. Introduction
what is optimization?
- An important tool in daily life, business and engineer
- Running a business: to maximize profit, minimize loss, maximize efficiency, or minimize risk.
- Design: minimize the weight of a bridge, and maximize the strength, within the design constrains; airplane engineering such as shape design and material selection, packing transistors in a computer chip in a functional way.
- Planning: select a flight route to minimize time or fuel consumption of an airplane
- Supermarket pricing and logistic
- Big data/AI
- Formal definition: to minimize (or maximize) a real function by deciding the values of free variables from within an allowed set.
Classification of optimization problems
- Continuous vs Discrete
- Constrained vs Unconstrained
- Global vs Local
- Stochastic vs Deterministic
- Convex vs Nonconvex
- Stochastic : random variable(DSPG)
- Convex has a lot of problem come in
- Convex form in range
- λ ∈ {0,1} (0~1)
Mathematical optimization
- optimal solution $x^*$ has smallest value of $f_0$ among all vectors that satisfy the constraints
Examples
- portfolio optimization
- variables: amounts invested in different assets
- constraints: budget, max./min. investment per asset, minimum return
- max/min : minimum could be zero, so we’re not allowed to actually purchase
- minimum return: we expect from this collection from this portfolio
- objective: overall risk or return variance
- ex) 500 stocks in can invest in, in my mean return absolutely muse excess 11% period
- device sizing in electronic circuits
- variables: device widths and lengths
- constraints: manufacturing limits, timing requirements, maximum area
- objective: power consumption
- data fitting
- variables: model parameters
- constraints: prior information, parameter limits
- objective: measure of misfit or prediction error
Examples
Examples
- Find two nonnegative numbers whose sum is up to 6 so that their product is a maximum.
- It is equivalent to find the largest area of a rectangular region provided that its perimeter is no greater than 12.
- Problem: let the two numbers be x, y, solve
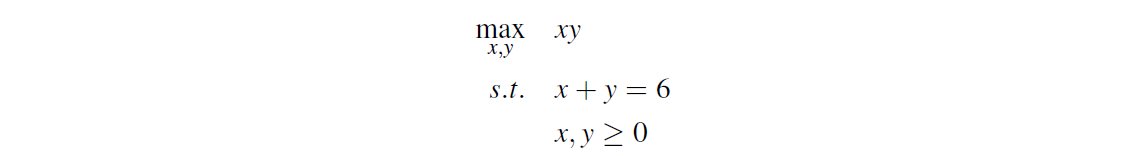
Examples
- Find a line that “best” fit three given points (x1, y1) = (2, 1), (x2, y2) = (3, 6) and (x3, y3) = (5, 4).
- Problem: let the line equation be y = ax + b, in the following least square sense:
Traveling sales man problem (TSMP)
- A salesman needs to visit a number (n) of cities, denoted by city 1, 2, · · · , n.
- The distances between cities are known, i.e. d_ij denotes the distance between city i and city j.
- The salesman wants to travel each city once in turn and in the meantime minimize the total travel distance.
- What order should be used?
- Problem: denote the order of travelling by ($i_1$, · · · , $i_n$), model
- this is polynomial time
Solving optimization problems
- general optimization problem (find a point: global optimization)
- very difficult to solve
- methods involve some compromise, e.g., very long computation time, or not always finding the solution
- exceptions : certain problem classes can be solved efficiently and reliably (Global solution)
- least-squares problems (we get the answer in period)
- linear programming problems (we get the answer in period)
- convex optimization problems (Global solution)
- most problem can not be optimized, but we use convex optimization solve the problem
- ex) singular values, principal component analysis
Convex optimization problem
- objective and constraint functions are convex:
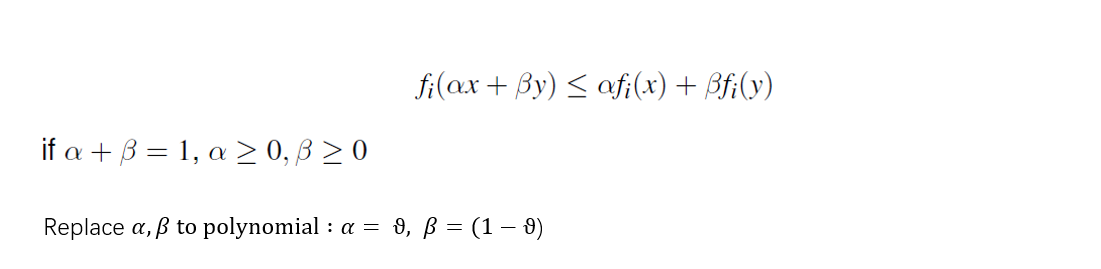
- includes least-squares problems and linear programs as special cases
- linear function are right on the boundary they have zero curvature(弯曲)
- so one way to say convex is just positive curvature(can solve problem)


Convex optimization problem
Convex optimization problem
- solving convex optimization problems
- no analytical solution
- reliable and efficient algorithms
- computation time (roughly) proportional to max{n3, n2m, F}, where F is cost of evaluating $f_i$’s and their first and second derivatives(this is basically square)
- almost a technology
- using convex optimization
Convex optimization example
- I have surface here with patches and I have some lamps here and we are going to choose the illumination powers in the lamps. that’s our variable. we’ll say the illumination on a patch here is going to be a sum of illumination from the lamps and it is going to be following proportional to the lamp power. and proportionality constant can be an inverse square law. R is the distance between patch and lamp, and there will be something which is a shading effect because obviously if we are coming in straight on. we get full power if this lamp for examples, put little illumination on here and if this were below it’s horizon if there were a lamp here, it would be not illuminate this patch at all
Least squares problems
Variants of Least squares
Linear Programming
- huge amount of qualitative intelligent things about linear program what we can not do is we can not write down formula for solution

- solving linear programs
- no analytical formula for solution ( there is no formula, there is no a transpose A inverse a transpose B)
- reliable and efficient algorithms and software
- computation time proportional to $n^2$m if m >= n; less with structure (same as least square)
- m : number of contain
- a mature technology
- a few standard tricks used to convert problems into linear programs
- e.g., problems involving $l_1$- or $l_∞$- norms, piecewise(分段)-linear functions


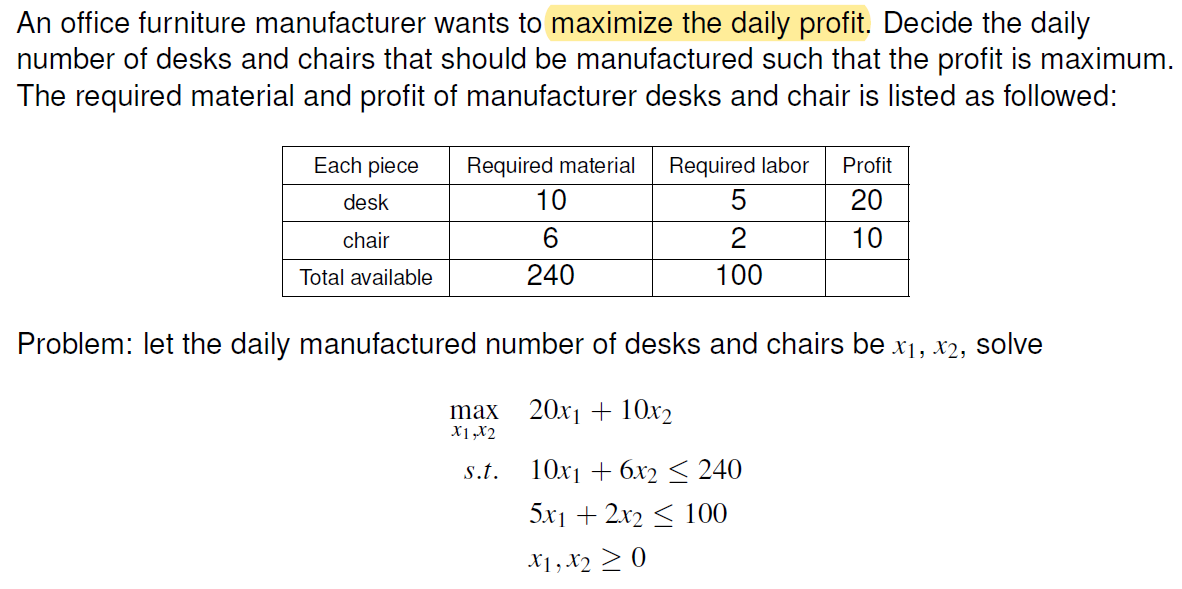
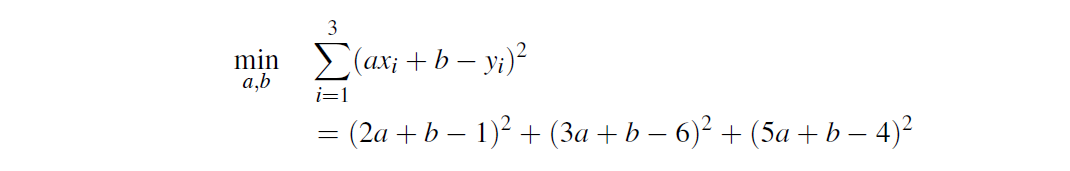

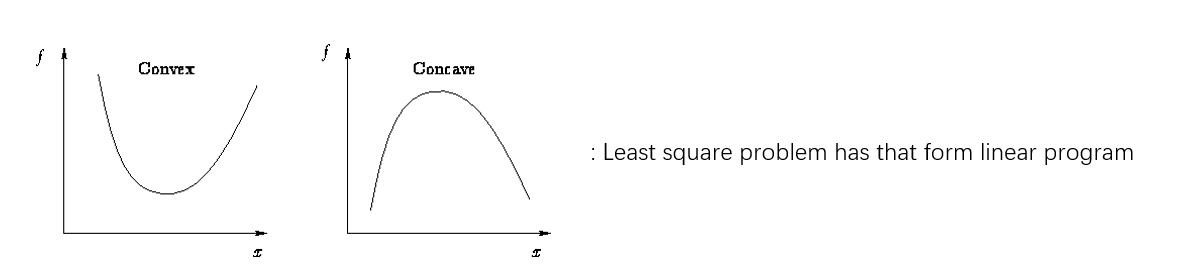
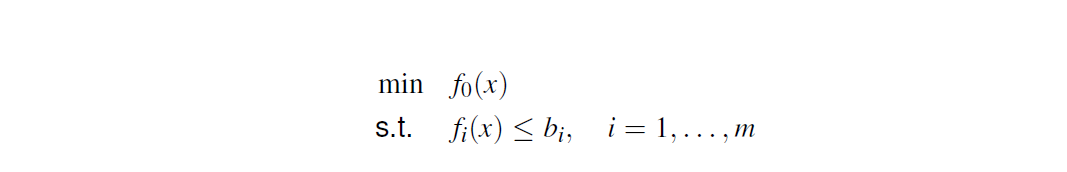


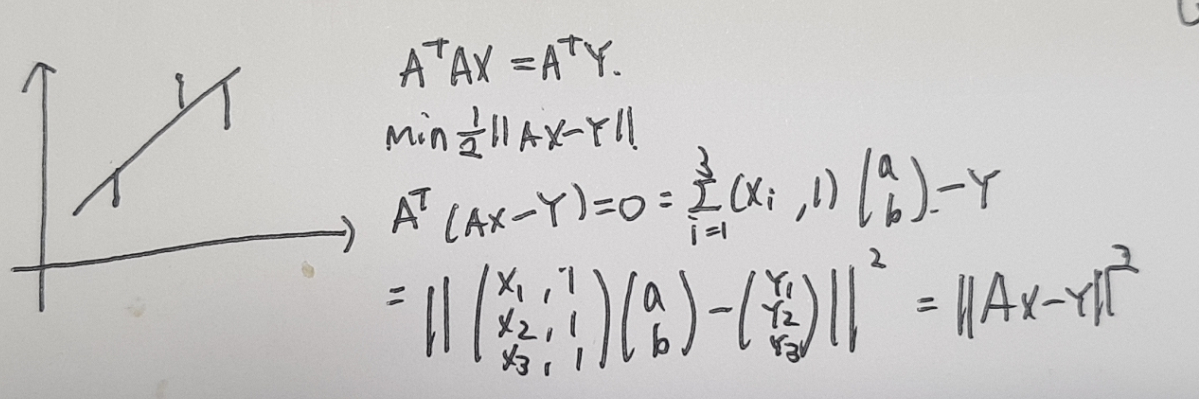






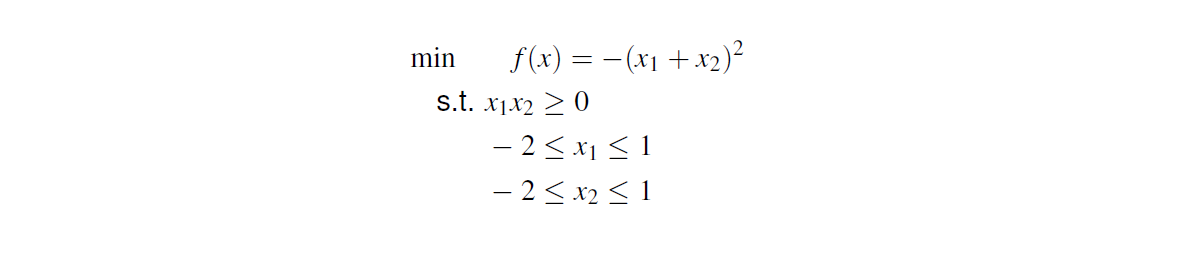
Comments