Optimization in Signal and Image processing
Model arising in compressive sensing and imaging sciences
- Separable(可分开的) Structures of problems
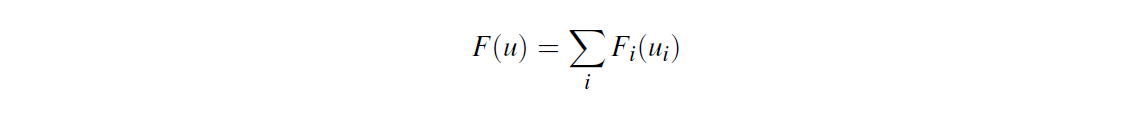
- Convexity and easy subproblems(子问题).
- Often involving large, nonsmooth convex functions with separable structure.
- First-order method can be very slow for producing high accuracy solutions, but also share many advantages:
- Non-differentiability
- Use minimal information, e.g.,(f;∇f)
- Often lead to very simple and “cheap” iterative schemes
- Complexity/iteration mildly dependent (e.g., linear) in problem’s dimension
- Suitable when high accuracy is not crucial [in many large scale applications, the data is anyway corrupted or known only roughly
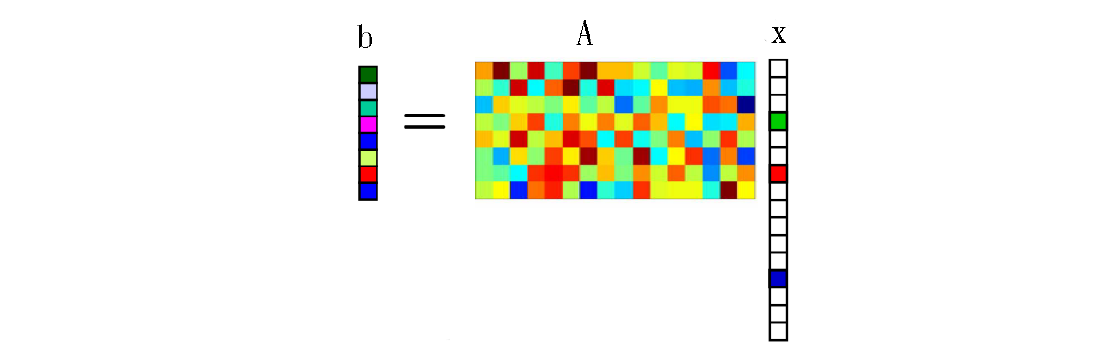
Example: compressive sensing(Kernel 같은 개념)
- Goal: Recover sparse signal from very few linear measurements.
- Basis pursuit model:
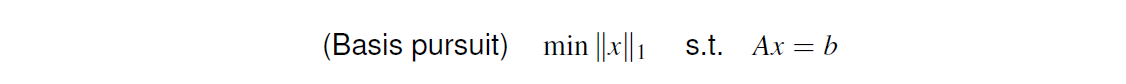
Compressive Sensing
- Find the sparest solution
- Given n=256, m=128.
- n is original signal
- m is output value
- A = randn(m,n); u = sprandn(n, 1, 0.1); b = A*u;
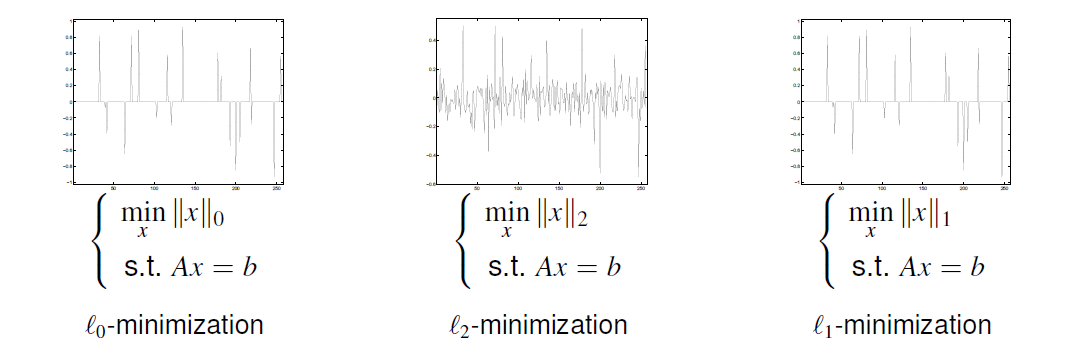
Sparse((흔히 넓은 지역에 분포된 정도가) 드문, (밀도가) 희박한) recovery models
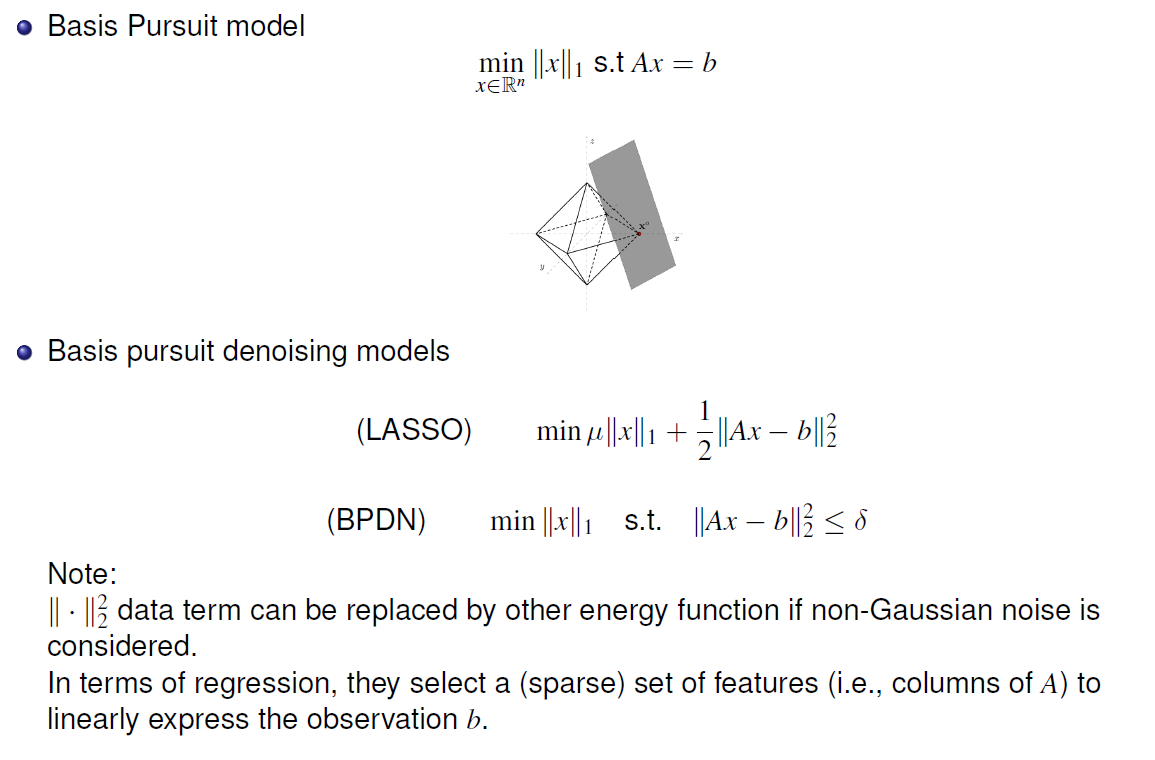
- Basis pursuit model : nonunique solution
- Ax = b = {$x^*$+N(A)} => ∀ v ∈ N(A), Av = 0
- μ is given parameter(constant variable)
Sparsity((흔히 넓은 지역에 분포된 정도가) 드문, (밀도가) 희박한) under a basis
- Given a reprenting basis or dictionary, we want to recover a signal which is sparse under this basis.
- Two types of models:

- Commonly used dictionaries include both analytic and trained ones.
- analytic bases: Id, DCT, wavelets, curvelets, gabor, etc., also their combinations; they have analytic properties, often easy to compute (for example, multiplying a vector takes O(n log n) instead of O($n^2$))
- data driven: can also be numerically learned from training data or partial signal, patches (offline or online learning).
- they can be orthogonal, frame, normalized or general.
- If Φ is orthogonal (or just invertible), the analyse based model is equivalent to synthesis based one by changing the variable. When it is not, the model is harder to solve.
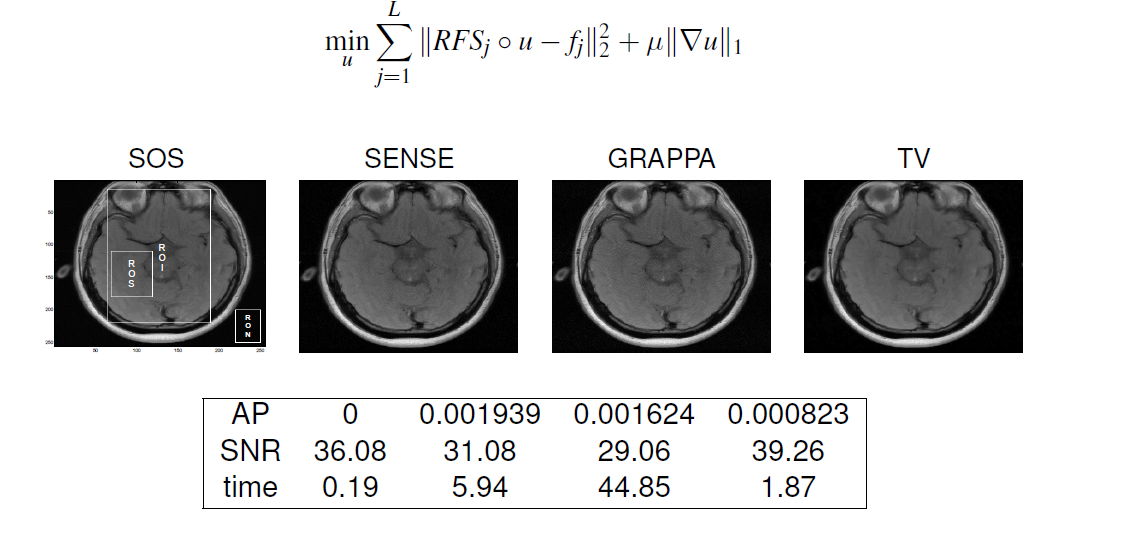
Parallel MRI reconstruction
Nonconvex sparsity models
- min f (x) + h(x)
- where either f or h is nonconvex or both are nonconvex. Some popular models:
- Nonlinear least square for nonlinear inverse problems f (x) = ‖F(x) − y‖^2.
- h(x) = ‖x‖_p, where 0 <= p < 1 or rank constraint.
- Alternating minimization methods in many applications, such as blind deconvolution, matrix factorization, or dictionary learning etc.
Optimization of Matrices
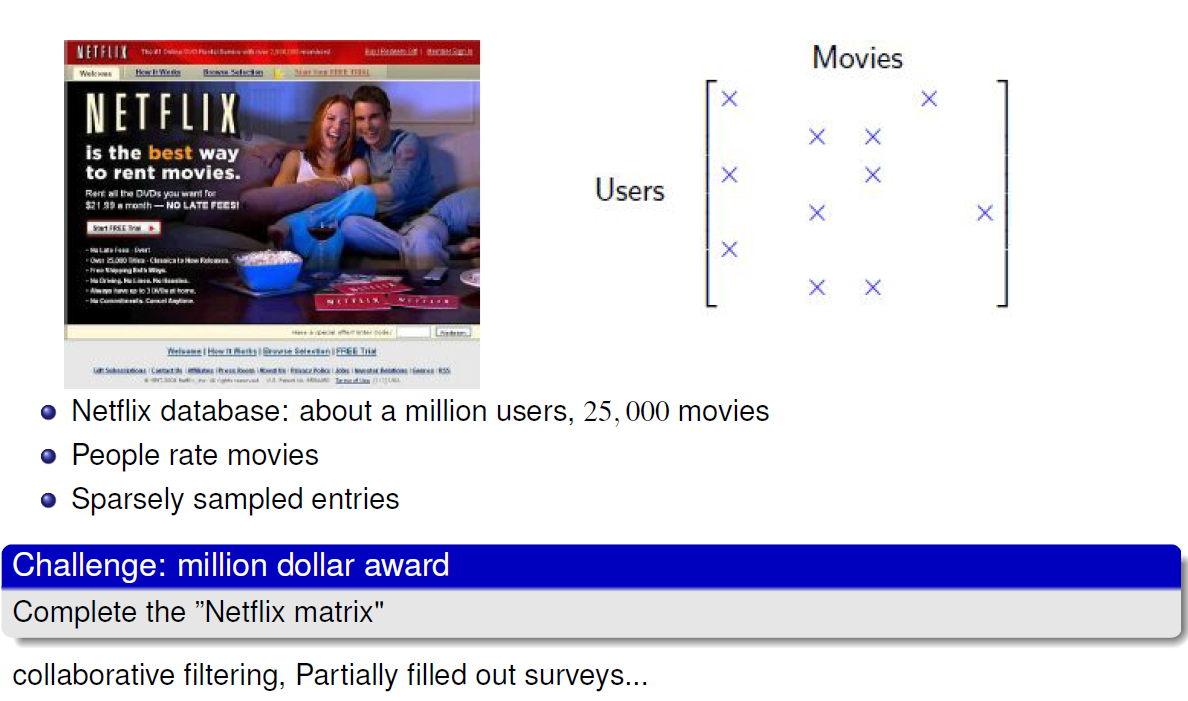
The Netflix problem
Matrix Rank Minimization

Video separation

Sparse and low-rank matrix separation
- Given a matrix M, we want to find a low rank matrix W and a sparse matrix E, so that W + E = M.
- Convex approximation:
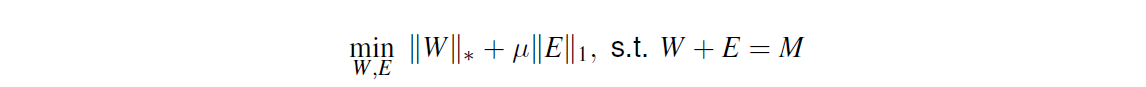
- Robust PCA (reduce dimension)
Extension

Correlation Matrices
- A correlation(相互关系) matrix satisfies:
- X = X^T , X_ii = 1, i = 1, . . . , n, X >= 0.
- Example: (low-rank) nearest correlation matrix estimation
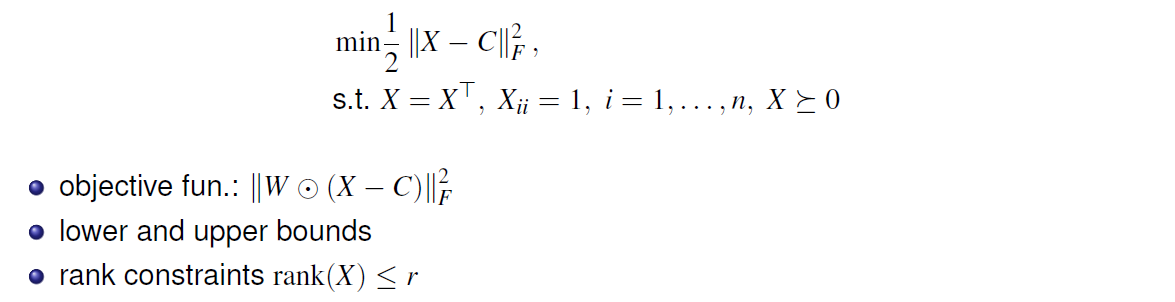
Optimization in Machine learning
Why Optimization in Machine Learning?

Loss functions in neural network

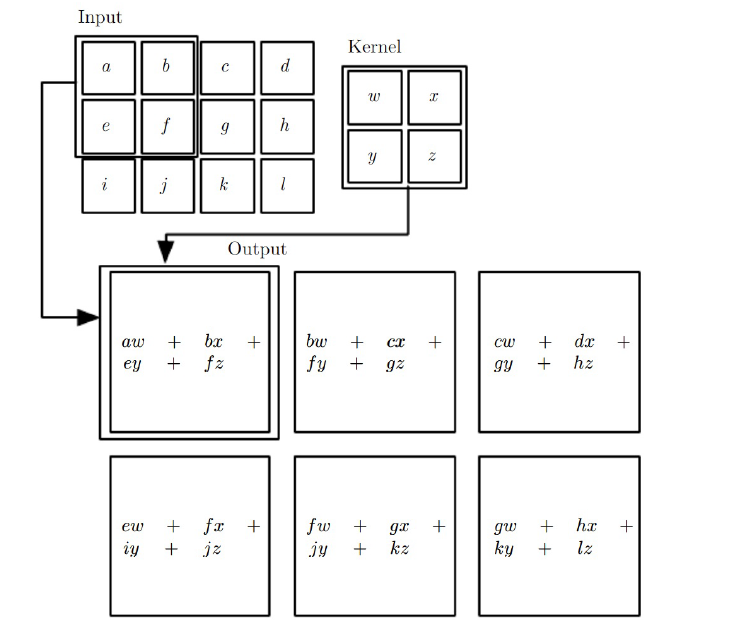
convolution operator
Optimization algorithms in Deep learning: stochastic gradient methods
- pytorch/caffe2: adadelta, adagrad, adam, nesterov, rmsprop, YellowFin https://github.com/pytorch/pytorch/tree/master/caffe2/sgd
- pytorch/torch: sgd, asgd, adagrad, rmsprop, adadelta, adam, adamax https://github.com/pytorch/pytorch/tree/master/torch/optim
- tensorflow: Adadelta, AdagradDA, Adagrad, ProximalAdagrad, Ftrl, Momentum, adam, Momentum, CenteredRMSProp https://github.com/tensorflow/tensorflow/blob/master/tensorflow/core/kernels/training_ops.cc
Generative adversarial network (GAN)

Reinforcement Learning
Optimization in Finance
Portfolio optimization

Review of Risk Measures

Reference
Optimization method - Standford University


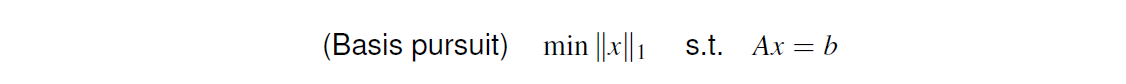







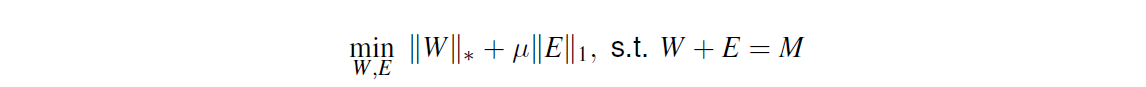

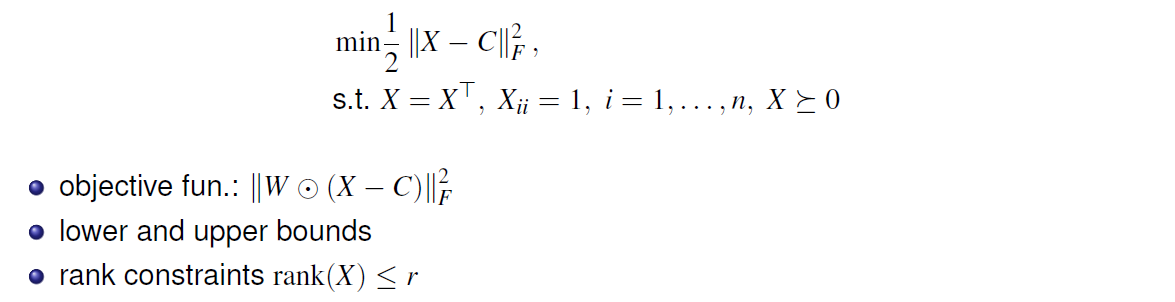







Comments