9. Newton's and Quansi-Newton methods
09 Oct 2019 | Optimization method
1. Features of Newton’s method
- Use both first and second derivatives.
- Based on local quadratic approximation to the objective function.
- Requires a positive Hessian to work.
- Converge quadratically under conditions.
2. Derivation of Newton’s method
- Rate of convergence is a measure of how fast the difference between the solution point and its estimates goes to zero. Faster algorithms usually use second-order information about the problem functions when calculating the search direction.
3. Two issues for Newton’s method
- When the dimension n is large, obtain F(x^(k)) and its inverse is computationally expensive => consider quasi-newton’s method
- Indefinite Hessian: the direction is not necessarily descending
4. Quasi Newton Method
- Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity.
- Newton’s method is one of the more successful algorithms for optimization
- If it converges, it has a quadratic order of convergence.
- However, as pointed out before, for a general nonlinear objective function, convergence to a solution cannot be guaranteed from an arbitrary initial point x^(0). In general, if the initial point is not sufficiently close to the solution, then the algorithm may not possess the descent
property
- Recall that the idea behind Newton’s method is to locally approximate the function f being minimized, at every iteration, by a quadratic function. The minimizer for the quadratic approximation is used as the starting point for the next iteration
- This leads to Newton’s recursive algorithm


5. THE BFGS ALGORITHM
- In 1970, an alternative update formula was suggested independently by Broyden, Fletcher, Goldfarb, and Shanno. The method is now called the BFGS algorithm, which we discuss in this section
- In numerical optimization, the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm is an iterative method for solving unconstrained nonlinear optimization problems
Optimization method - Standford University
https://www.youtube.com/results?search_query=convex+function
1. Features of Newton’s method
- Use both first and second derivatives.
- Based on local quadratic approximation to the objective function.
- Requires a positive Hessian to work.
- Converge quadratically under conditions.
2. Derivation of Newton’s method
- Rate of convergence is a measure of how fast the difference between the solution point and its estimates goes to zero. Faster algorithms usually use second-order information about the problem functions when calculating the search direction.
3. Two issues for Newton’s method
- When the dimension n is large, obtain F(x^(k)) and its inverse is computationally expensive => consider quasi-newton’s method
- Indefinite Hessian: the direction is not necessarily descending
4. Quasi Newton Method
- Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity.
- Newton’s method is one of the more successful algorithms for optimization
- If it converges, it has a quadratic order of convergence.
- However, as pointed out before, for a general nonlinear objective function, convergence to a solution cannot be guaranteed from an arbitrary initial point x^(0). In general, if the initial point is not sufficiently close to the solution, then the algorithm may not possess the descent property
- Recall that the idea behind Newton’s method is to locally approximate the function f being minimized, at every iteration, by a quadratic function. The minimizer for the quadratic approximation is used as the starting point for the next iteration
- This leads to Newton’s recursive algorithm


5. THE BFGS ALGORITHM
- In 1970, an alternative update formula was suggested independently by Broyden, Fletcher, Goldfarb, and Shanno. The method is now called the BFGS algorithm, which we discuss in this section
- In numerical optimization, the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm is an iterative method for solving unconstrained nonlinear optimization problems
Optimization method - Standford University
https://www.youtube.com/results?search_query=convex+function
















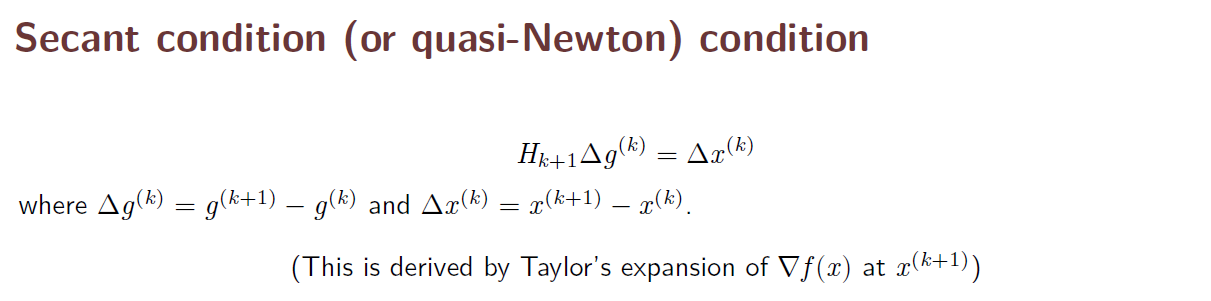

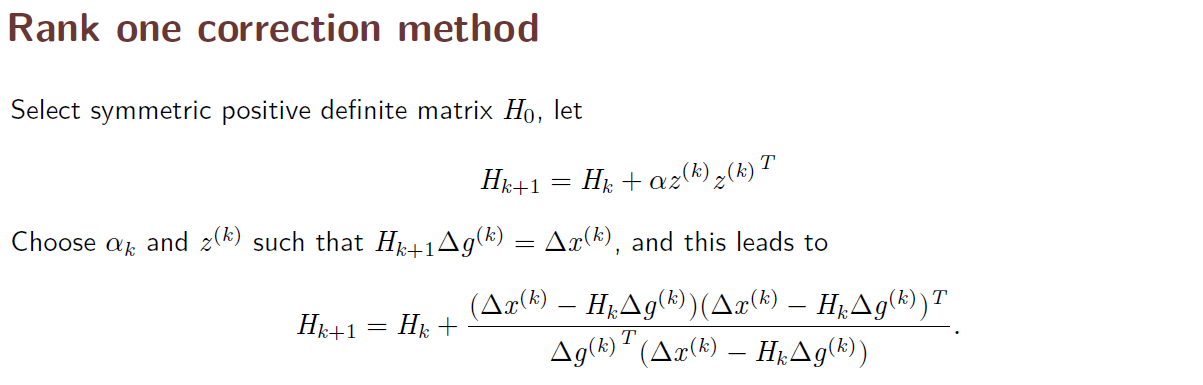





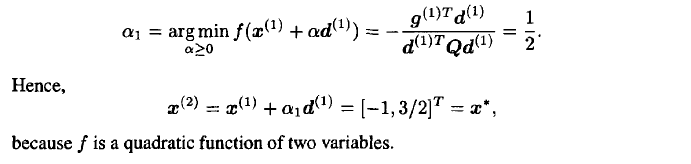






Comments