7. The Value function
24 Sep 2019 | Reinforcement Learning
The Value function
1. Assigning Rewards
- the programmers are like “coaches(教练)” to the AI
- Pet Owner is a good analogy
- We define how to give rewards to agent (Ex. Give same reward no matter what agent does - agent will always just behave randomly)(Ex2. Give our dog a treat when it behaves badly - encourages bad behavior)
2. Maze Example
- Robot Trying to solve maze
- Reward of 1 for finding the maze exit, else 0
- But robot unlikely to solve the maze with this structure
- if robot only sees reward is the max reward if all we see is 0
- better: Every step yields reward of -1
- Now robot is encouraged so solve maze as quickly as possible
3. Something like
- be careful not to build our own prior knowledge into the AI ( Ex. Chess)
- Agent should be rewarded for winning, not taking opponent’s pieces
- No reward for implementing strategy us read about in chess book
- Free the agent to find its own solution
- OK to lose all but one piece and then win
- tell the agent what we want it to achieve, not how we want it to be achieved
4. Planning
- Scenario: we are thinking about studying for tomorrow’s exam. we would rather hang out with friends.
- hangout with friends -> dopamine hit -> happy
- Study -> feel tired and bored
- why study?
- we don’t think about immediate rewards, but future rewards too. we want to assign some value to the current state that reflects the future too. call this the “VALUE FUNCTION”
5. Credit Assignment Problem
- we receive a reward - getting hired for our dream job
- what previous action led to this success
- that called the “Credit Assignment Problem”
- Ask the Question: “What did I do in the past that led to the reward I’m receiving now “
- what action gets the credit
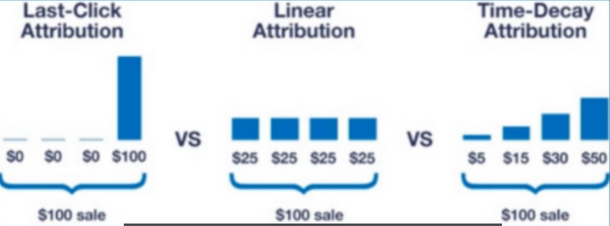
6. Attribution
- Related to online advertising concept of attribution
- if we show the user the same ad 10 times before they buy, which ad gets the credit?
- In RL we don’t just assign ad-hoc(点对点) like this
7. Delayed Rewards
- Delayed Rewards: another way of thinking of the same thing
- Credit assignment: Present -> Past
- Delayed from the other direction: Present -> Future
- Related to field known as “planning”
- the idea of delayed rewards tell us that an AI needs to have the ability of foresight or planning, planning is actually a field of study that crosses over with reinforcement learning
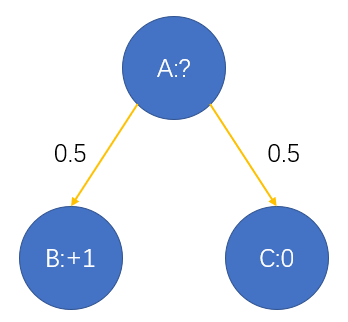
8. Scenario
- 2 possible next states from A: B or C
- 50% probability of ending up in either
- Reasonable value of A?
- Value(A) = 0.5x1 + 0.5x0 = 0.5
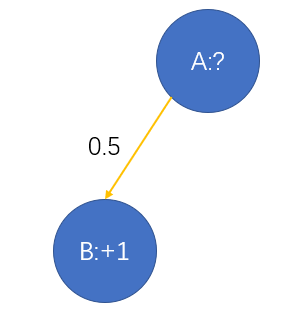
- 1 Possible next state form A:B
- 100% Probability of ending up in B
- Reasonable value for A ?
- Value(A) = 1 x 1 = 1
- Value tells us the “Future goodness” of a state
9. Value Function
- V(s) - The Value(Taking into Account the probability of all possible future rewards) of a state
- Value is a measure of possible future rewards we may get from being in this state
- reward is immediate(Ex. Jumping on a Goomba will immediately increase our score)(Ex2. Standing in front of a Goomba will not increase our score, but will put us in a position to jump in the next few states)
- Estimating the value function is a central task in RL
- Not RL algorithms require it(Ex, Evolutionary algorithm that mutates & spawns offspring, only those who survive the longest make it to next generation)
- by pure evolution + natural selection we can breed better and better agents
- but not the type of algorithm we are interested in for RL most of the time
10. Efficiency
- the Value function is a fast & efficient way of searching the game tree
- time consuming to enumerate every possible state transition and their probabilities of occurring.
- tic-tac-toe: 3^(3*3) = 19683
- Connect 4: 3^(4*4) = 43Millon
- Exponential Growth is never good
- Curse of dimensionality
- V(S) gives answer instantly O(1)
11. Finding V(s)
-
V(s) = E[all future rewards
S(t) = s]
- E[x] = average of X
- this is generic algorithm here
- so we need to introduce some constraints here
- iterative algorithm
- initialize V(s):
- V(s) = 1 if s = winning rate
- V(s) = 0 if s = lose or draw
- V(s) = 0.5 otherwise
- when we study “real” algorithm, we won’t need such careful initialization
- V(s) can be interpreted(说明) as probability of winning after arriving in s( for this game only )(S.t V(s) is winning rate )
- After we initialize V(s), we update it as follows

- s = current state, s’=next state
- s represents every state we encounter in an episode
- Means we need to actually play an episode and keep track of state history
- terminal state never updated since it doesn’t have a next state
- we’ll do this over many episode
pseudocode
for t in range(max_iterations):
state_history = play_game
for(s,s') in state_history from end to start:
V(s) = V(s) + learning_rate*(V(s')-V(s))
12. Playing the Game
- how do we actually play the game/generate an episode
- Take random action? No!
- we don’t need to, we have the value function
maxV = 0
maxA = None
for a,s' in possible_next_states:
if V(s') > maxV :
maxV = V(s') # 좋은 max Value를 골랐으니 다음에 나오는 station이 된다.
maxA = a
perform action max A
Note : would taking random actions even give us the right value functions? No, Because a game tree w/ random actions has different probabilities than a game tree w/ “best” actions
13. Problem
- Problem with previous approach: Value function isn’t accurate
- if we had the true value function, we wouldn’t need to do any of this work
- Example of the explore-exploit dilemma
- Random actions lead us to states we may not have otherwise visited
- we can thus improve our value estimate for those states
- but to win, we need to do the action that yields maximum value
- we will use upsilon-greedy
14. Intuition
- should remind you of the low-pass-filter / average-value-finding equation we saw earlier(+ gradient descent if we’ve seen that)
- since we visit the states stochastically(随机地), V(s) will try to get close to V(s’) for all possible next s’
- by playing infinitely many episodes, the proportion of time we spend in each’s will approach the true probabilities
- Extremely Important detail, hard to discern(识别) from update equation alone
- what order to update V(s)?
- Key: We’re moving V(s) closer to V(s’)
- Therefore we want V(s’) to be more accurate than V(s)
- V(terminal) = 0, 1
- For all others, if V(s’) is no better than V(s), this update doesn’t help
- therefore, update goes backwards along state history
15. Summary
- Credit assignment problem/ delayed rewards
- Value function for representing future reward
- value function efficiency vs searching game tree
- iterative algorithm to find the value function
- warning! Not the “formal” value function.
- Everything in tic-tac-toe section is informal, designed to get us acquainted(熟悉) with solving a RL Problem
Reference:
Artificial Intelligence Reinforcement Learning
The Value function
1. Assigning Rewards
- the programmers are like “coaches(教练)” to the AI
- Pet Owner is a good analogy
- We define how to give rewards to agent (Ex. Give same reward no matter what agent does - agent will always just behave randomly)(Ex2. Give our dog a treat when it behaves badly - encourages bad behavior)
2. Maze Example
- Robot Trying to solve maze
- Reward of 1 for finding the maze exit, else 0
- But robot unlikely to solve the maze with this structure
- if robot only sees reward is the max reward if all we see is 0
- better: Every step yields reward of -1
- Now robot is encouraged so solve maze as quickly as possible
3. Something like
- be careful not to build our own prior knowledge into the AI ( Ex. Chess)
- Agent should be rewarded for winning, not taking opponent’s pieces
- No reward for implementing strategy us read about in chess book
- Free the agent to find its own solution
- OK to lose all but one piece and then win
- tell the agent what we want it to achieve, not how we want it to be achieved
4. Planning
- Scenario: we are thinking about studying for tomorrow’s exam. we would rather hang out with friends.
- hangout with friends -> dopamine hit -> happy
- Study -> feel tired and bored
- why study?
- we don’t think about immediate rewards, but future rewards too. we want to assign some value to the current state that reflects the future too. call this the “VALUE FUNCTION”
5. Credit Assignment Problem
- we receive a reward - getting hired for our dream job
- what previous action led to this success
- that called the “Credit Assignment Problem”
- Ask the Question: “What did I do in the past that led to the reward I’m receiving now “
- what action gets the credit
6. Attribution
- Related to online advertising concept of attribution
- if we show the user the same ad 10 times before they buy, which ad gets the credit?
- In RL we don’t just assign ad-hoc(点对点) like this

7. Delayed Rewards
- Delayed Rewards: another way of thinking of the same thing
- Credit assignment: Present -> Past
- Delayed from the other direction: Present -> Future
- Related to field known as “planning”
- the idea of delayed rewards tell us that an AI needs to have the ability of foresight or planning, planning is actually a field of study that crosses over with reinforcement learning
8. Scenario
- 2 possible next states from A: B or C
- 50% probability of ending up in either
- Reasonable value of A?
- Value(A) = 0.5x1 + 0.5x0 = 0.5
- 1 Possible next state form A:B
- 100% Probability of ending up in B
- Reasonable value for A ?
- Value(A) = 1 x 1 = 1
- Value tells us the “Future goodness” of a state
9. Value Function
- V(s) - The Value(Taking into Account the probability of all possible future rewards) of a state
- Value is a measure of possible future rewards we may get from being in this state
- reward is immediate(Ex. Jumping on a Goomba will immediately increase our score)(Ex2. Standing in front of a Goomba will not increase our score, but will put us in a position to jump in the next few states)
- Estimating the value function is a central task in RL
- Not RL algorithms require it(Ex, Evolutionary algorithm that mutates & spawns offspring, only those who survive the longest make it to next generation)
- by pure evolution + natural selection we can breed better and better agents
- but not the type of algorithm we are interested in for RL most of the time
10. Efficiency
- the Value function is a fast & efficient way of searching the game tree
- time consuming to enumerate every possible state transition and their probabilities of occurring.
- tic-tac-toe: 3^(3*3) = 19683
- Connect 4: 3^(4*4) = 43Millon
- Exponential Growth is never good
- Curse of dimensionality
- V(S) gives answer instantly O(1)
11. Finding V(s)
-
V(s) = E[all future rewards S(t) = s] - E[x] = average of X
- this is generic algorithm here
- so we need to introduce some constraints here
- iterative algorithm
- initialize V(s):
- V(s) = 1 if s = winning rate
- V(s) = 0 if s = lose or draw
- V(s) = 0.5 otherwise
- when we study “real” algorithm, we won’t need such careful initialization
- V(s) can be interpreted(说明) as probability of winning after arriving in s( for this game only )(S.t V(s) is winning rate )
- After we initialize V(s), we update it as follows

- s = current state, s’=next state
- s represents every state we encounter in an episode
- Means we need to actually play an episode and keep track of state history
- terminal state never updated since it doesn’t have a next state
- we’ll do this over many episode
pseudocode
for t in range(max_iterations):
state_history = play_game
for(s,s') in state_history from end to start:
V(s) = V(s) + learning_rate*(V(s')-V(s))
12. Playing the Game
- how do we actually play the game/generate an episode
- Take random action? No!
- we don’t need to, we have the value function
maxV = 0
maxA = None
for a,s' in possible_next_states:
if V(s') > maxV :
maxV = V(s') # 좋은 max Value를 골랐으니 다음에 나오는 station이 된다.
maxA = a
perform action max A
Note : would taking random actions even give us the right value functions? No, Because a game tree w/ random actions has different probabilities than a game tree w/ “best” actions
13. Problem
- Problem with previous approach: Value function isn’t accurate
- if we had the true value function, we wouldn’t need to do any of this work
- Example of the explore-exploit dilemma
- Random actions lead us to states we may not have otherwise visited
- we can thus improve our value estimate for those states
- but to win, we need to do the action that yields maximum value
- we will use upsilon-greedy
14. Intuition
- should remind you of the low-pass-filter / average-value-finding equation we saw earlier(+ gradient descent if we’ve seen that)
- since we visit the states stochastically(随机地), V(s) will try to get close to V(s’) for all possible next s’
- by playing infinitely many episodes, the proportion of time we spend in each’s will approach the true probabilities
- Extremely Important detail, hard to discern(识别) from update equation alone
- what order to update V(s)?
- Key: We’re moving V(s) closer to V(s’)
- Therefore we want V(s’) to be more accurate than V(s)
- V(terminal) = 0, 1
- For all others, if V(s’) is no better than V(s), this update doesn’t help
- therefore, update goes backwards along state history
15. Summary
- Credit assignment problem/ delayed rewards
- Value function for representing future reward
- value function efficiency vs searching game tree
- iterative algorithm to find the value function
- warning! Not the “formal” value function.
- Everything in tic-tac-toe section is informal, designed to get us acquainted(熟悉) with solving a RL Problem
Reference:
Artificial Intelligence Reinforcement Learning





Comments