8. Tic-Tac-Toe
25 Sep 2019 | Reinforcement Learning
1. Outline
2. representing States
- last post, I told you this would be an O(1) lookup (as in an array )
- Possible solution: Convert the board to tuple of tuples, use as dictionary Key
- Better: Map Each state to a number, use numpy array
3. Mapping state to a number
- there are 3 state, “O”, “X”, “Empty”
- 9 array so all possible state is 3^9 = 19683
- overhead not a problem, these states are unreachable(e.g. 3x’s in a row and 3o’s in a row on the same board)
- Should remind us of binary numbers(2 Possible symbols in each location vs 3)
- binary to decimal(小数):

- For us:
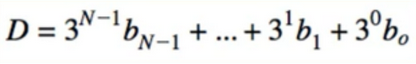
In code
k=0
h=0
for i in xrange(Length):
for j in xrange(Length):
if self.board[i,j] == 0:
v = 0
elif self.board[i,j] == self.x:
v = 1
elif self.board[i,j] == self.o:
v = 2
h + = (3**k)*v
k + = 1
4. Initializing the value function
- Recall, we initialize V(s) as :
- 1 if s == winning terminal state
- 0 if s == lose or draw terminal state
- 0.5 otherwise
- how do we find all the “s”?
5. Enumerating state
- lets think which is better ?
1) Create a “game tree “ of all possible in the game?
2) Create a permutation(排列) of all possible settings of all possible positions on the board?
Game Tree
- Problem : redundant states
- i.e. see the same state more than once in the tree
Start: 9 choices
then: 8 choices
then: 7 choices
….
9! = 362880 » 3^9
permutation(순열)
- How? think binary first:
- Generate permutation of Length N:
0 + Generate permutation of length N -1
1 + Generate Permutation of Length N - 1
def generate_all_binary_numbers(N):
results = {}
child_results = generate_all_binary_numbers(N-1)
for prefix in ('0', '1'):
for suffix in child_results:
new_result = prefix + suffix
returns.append(new_result)
return results
(base case not shown for simplicity)
- if don’t get about this please check in here
Enumerating States Recursively
- that is all combinations of inputs an programs that halt
- Function: get_state_hash_and_winner
- Returns : List of triples(state, winner, ended)
- state : configuration of the board as a hashed int
- Winner is None if ended is False (즉 승자가 나올떄 까지 계속 돈다)
- inputs : env, i, j
max_length=0
while(true):
max_length = max_length +1
for each program "P" of length <= max_length: # P is finite
for each input "I" of length <= max_length:
if "env" halts on 'I' after max_length steps:
print P,I
Summary
- In order to initialize V(s) to our desired values, we must enumerate all the states
- we can either search the game tree(9!) or find board permutations($3^9$)
- 9! is super-exponential
- Enumerating game states Recursively
- initializing V(s) is different for X and O
6. The Environment Class(Code)
Method: __init__() : #initialize Important instance vars
is_empthy(i,j): # returns true if(i,j) is empty
reward(symbol)
get_state()
game_over()
draw_board()
Constructor
class Environment:
def __init__(self):
self.board = np.zeros((length, length))
self.x = -1 # represents an x on the board, player 1
self.o = 1 # represents an o on the board player 2
self.winner = None
self.ended = False
self.num_states = 3**(length*length)
is_empthy
def is_empthy(self, i, j):
return self.board[i,j] == 0
reward
def reward(self, sym):
# no reward until game is over
if not self.game_over():
return 0
# if we get here, game is over
# sym will be self.x or self.o
return 1 if self.winner == sym else 0
get_state
def get_state(self):
# returns the current state, represented as an int
# from 0...|S|-1, where S = set of all possible states
# |S| = 3^(BOARD SIZE), since each cell can have 3 possible values - empty, x, o
# some states are not possible, e.g. all cells are x, but we ignore that detail
# this is like finding the integer represented by a base-3 number
k = 0
h = 0
for i in range(LENGTH):
for j in range(LENGTH):
if self.board[i,j] == 0:
v = 0
elif self.board[i,j] == self.x:
v = 1
elif self.board[i,j] == self.o:
v = 2
h += (3**k) * v # Value Funtion
k += 1
return h
game_over
def game_over(self, force_recalculate==False):
if not force_recalculate and self.ended:
return self.ended
# check rows
for i in range(LENGTH):
for player in (self.x, self.o):
if self.board[i].sum() == player*LENGTH:
self.winner = player
self.ended = True
return True
# check columns
for j in range(LENGTH):
for player in (self.x, self.o):
if self.board[:,j].sum() == player*LENGTH:
self.winner = player
self.ended = True
return True
# check diagonals
for player in (self.x, self.o):
# top-left -> bottom-right diagonal
if self.board.trace() == player*LENGTH:
self.winner = player
self.ended = True
return True
# top-right -> bottom-left diagonal
if np.fliplr(self.board).trace() == player*LENGTH:
self.winner = player
self.ended = True
return True
# check if draw
if np.all((self.board == 0) == False):
# winner stays None
self.winner = None
self.ended = True
return True
# game is not over
self.winner = None
return False
draw_board
def draw_board(self):
for i in range(LENGTH):
print("-------------")
for j in range(LENGTH):
print(" ", end="")
if self.board[i,j] == self.x:
print("x ", end="")
elif self.board[i,j] == self.o:
print("o ", end="")
else:
print(" ", end="")
print("")
print("-------------")
7. The Agent class
- Contains the AI
- different from supervised/unsupervised ML, because we don’t just feed it data
- it has to interact with the Environment
- one-line update for V(s) is a very small part of the agent, yet responsible for 100% of its intelligence
The Agent Class
class Agent:
def __init__(self, eps=0.1, alpha=0.5):
self.eps = eps # probability of choosing random action instead of greedy
self.alpha = alpha # learning rate
self.verbose = False
self.state_history = []
def setV(self, V): # SetV is the allow us to initialize the value function
self.V = V
def set_symbol(self, sym): # symbol is allow us to give this agent a symbol that it'll use to play on the board
self.sym = sym
def set_verbose(self, v):
# if true, will print values for each position on the board
self.verbose = v
def reset_history(self):
self.state_history = []
Take_action
def take_action(self, env):
# choose an action based on epsilon-greedy strategy
r = np.random.rand()
best_state = None
if r < self.eps:
# take a random action
if self.verbose:
print("Taking a random action")
possible_moves = []
for i in range(LENGTH):
for j in range(LENGTH):
if env.is_empty(i, j):
possible_moves.append((i, j))
idx = np.random.choice(len(possible_moves))
next_move = possible_moves[idx]
else:
# choose the best action based on current values of states
# loop through all possible moves, get their values
# keep track of the best value
pos2value = {} # for debugging
next_move = None
best_value = -1
for i in range(LENGTH):
for j in range(LENGTH):
if env.is_empty(i, j):
# what is the state if we made this move?
env.board[i,j] = self.sym
state = env.get_state()
env.board[i,j] = 0 # don't forget to change it back!
pos2value[(i,j)] = self.V[state]
if self.V[state] > best_value:
best_value = self.V[state]
best_state = state
next_move = (i, j)
# if verbose, draw the board w/ the values
if self.verbose:
print("Taking a greedy action")
for i in range(LENGTH):
print("------------------")
for j in range(LENGTH):
if env.is_empty(i, j):
# print the value
print(" %.2f|" % pos2value[(i,j)], end="")
else:
print(" ", end="")
if env.board[i,j] == env.x:
print("x |", end="")
elif env.board[i,j] == env.o:
print("o |", end="")
else:
print(" |", end="")
print("")
print("------------------")
# make the move
env.board[next_move[0], next_move[1]] = self.sym
update_state_history
def update_state_history(self, s):
# cannot put this in take_action, because take_action only happens
# once every other iteration for each player
# state history needs to be updated every iteration
# s = env.get_state() # don't want to do this twice so pass it in
self.state_history.append(s)
update
def update(self, env):
# we want to BACKTRACK over the states, so that:
# V(prev_state) = V(prev_state) + alpha*(V(next_state) - V(prev_state))
# where V(next_state) = reward if it's the most current state
#
# NOTE: we ONLY do this at the end of an episode
# not so for all the algorithms we will study
reward = env.reward(self.sym)
target = reward
for prev in reversed(self.state_history):
value = self.V[prev] + self.alpha*(target - self.V[prev])
self.V[prev] = value
target = value
self.reset_history()
8. The Human Class(Code)
Human class
class Human:
def __init__(self):
pass
def set_symbol(self, sym):
self.sym = sym
def take_action(self, env):
while True:
# break if we make a legal move
move = input("Enter coordinates i,j for your next move (i,j=0..2): ")
i, j = move.split(',')
i = int(i)
j = int(j)
if env.is_empty(i, j):
env.board[i,j] = self.sym
break
def update(self, env):
pass
def update_state_history(self, s):
pass
# recursive function that will return all
# possible states (as ints) and who the corresponding winner is for those states (if any)
# (i, j) refers to the next cell on the board to permute (we need to try -1, 0, 1)
# impossible games are ignored, i.e. 3x's and 3o's in a row simultaneously
# since that will never happen in a real game
play games
def play_game(p1, p2, env, draw=False):
# loops until the game is over
current_player = None
while not env.game_over():
# alternate between players
# p1 always starts first
if current_player == p1:
current_player = p2
else:
current_player = p1
# draw the board before the user who wants to see it makes a move
if draw:
if draw == 1 and current_player == p1:
env.draw_board()
if draw == 2 and current_player == p2:
env.draw_board()
# current player makes a move
current_player.take_action(env)
# update state histories
state = env.get_state()
p1.update_state_history(state)
p2.update_state_history(state)
if draw:
env.draw_board()
# do the value function update
p1.update(env)
p2.update(env)
Main
if __name__ == '__main__':
# train the agent
p1 = Agent()
p2 = Agent()
# set initial V for p1 and p2
env = Environment()
state_winner_triples = get_state_hash_and_winner(env)
Vx = initialV_x(env, state_winner_triples)
p1.setV(Vx)
Vo = initialV_o(env, state_winner_triples)
p2.setV(Vo)
# give each player their symbol
p1.set_symbol(env.x)
p2.set_symbol(env.o)
T = 10000 #train
for t in range(T):
if t % 200 == 0:
print(t)
play_game(p1, p2, Environment())
# play human vs. agent
# do you think the agent learned to play the game well?
# human Verification
human = Human()
human.set_symbol(env.o)
while True:
p1.set_verbose(True)
play_game(p1, human, Environment(), draw=2)
# I made the agent player 1 because I wanted to see if it would
# select the center as its starting move. If you want the agent
# to go second you can switch the human and AI.
answer = input("Play again? [Y/n]: ")
if answer and answer.lower()[0] == 'n':
break
9. Summary
- Would not be able to increase intelligence by learning from experience
- would not be generalizable to other Environments
- Components of a RL system (Agent, Environment, state, action, reward)
- Episodes, terminal states
- Choosing rewards carefully
- credit assignment(움직임에 따라 승리의 확율을 나타낸다)
- Delayed Reward
- Planning intelligently to maximize overall rewards
- Value function
- V(s) <- V(s) + α(V(s’)- V(s))
RL vs SL
- why not use a supervised learning model that maps states -> actions directly
- i.e model y = f(x) where x = state, y= action
- how would we come up with labels?
- very easy for state space to grow too large to enumerate
- connect-4/ tic-tac-toe is probably the limit
- imagine: HD graphics 60 FPS video game - we can’t even conceptualize how large the state space
- thus, how could we create a label for every state?
- Rewards are delayed(데이터가 없는 상태에서 액션을 즉시 선택하는 것은 올바르지 않기 때문에, 데이터를 쌓은 상태에서 액션을 취하려 Reward Delayed를 한다)
- but in Rl value function has the “future” built into it
- if doing SL, and somehow manage to get around a humongous(巨大的) state-space, how would we choose the right actions?
- instead of letting the value function take care of measuring the future, we need to somehow keep track of what’s best for all future possibilities
- Rewards can have component of randomness. (E.g same state gives reward of 1 or 0 )(E.g2. we study for our exam tomorrow, then there is a snow storm and our exam is canceled)
- Next states can also be random
- In RL, we are never told if a state-action pair is good or not
- the only way we can find out is if we “discover” it ourselves by performing the action
- RL is online. after each episode of tic-tac-toe, we get better
- compare to decision tree - a tree is made based on entire training set
- if we want to incorporate new data, start training all over again
Reference:
Artificial Intelligence Reinforcement Learning
1. Outline
2. representing States
- last post, I told you this would be an O(1) lookup (as in an array )
- Possible solution: Convert the board to tuple of tuples, use as dictionary Key
- Better: Map Each state to a number, use numpy array
3. Mapping state to a number
- there are 3 state, “O”, “X”, “Empty”
- 9 array so all possible state is 3^9 = 19683
- overhead not a problem, these states are unreachable(e.g. 3x’s in a row and 3o’s in a row on the same board)
- Should remind us of binary numbers(2 Possible symbols in each location vs 3)
- binary to decimal(小数):

- For us:
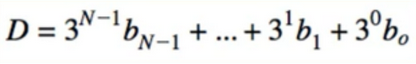
In code
k=0
h=0
for i in xrange(Length):
for j in xrange(Length):
if self.board[i,j] == 0:
v = 0
elif self.board[i,j] == self.x:
v = 1
elif self.board[i,j] == self.o:
v = 2
h + = (3**k)*v
k + = 1
4. Initializing the value function
- Recall, we initialize V(s) as :
- 1 if s == winning terminal state
- 0 if s == lose or draw terminal state
- 0.5 otherwise
- how do we find all the “s”?
5. Enumerating state
- lets think which is better ? 1) Create a “game tree “ of all possible in the game? 2) Create a permutation(排列) of all possible settings of all possible positions on the board?
Game Tree
- Problem : redundant states
- i.e. see the same state more than once in the tree
Start: 9 choices then: 8 choices then: 7 choices ….
9! = 362880 » 3^9
permutation(순열)
- How? think binary first:
- Generate permutation of Length N:
0 + Generate permutation of length N -1
1 + Generate Permutation of Length N - 1
def generate_all_binary_numbers(N):
results = {}
child_results = generate_all_binary_numbers(N-1)
for prefix in ('0', '1'):
for suffix in child_results:
new_result = prefix + suffix
returns.append(new_result)
return results
(base case not shown for simplicity)
- if don’t get about this please check in here
Enumerating States Recursively
- that is all combinations of inputs an programs that halt
- Function: get_state_hash_and_winner
- Returns : List of triples(state, winner, ended)
- state : configuration of the board as a hashed int
- Winner is None if ended is False (즉 승자가 나올떄 까지 계속 돈다)
- inputs : env, i, j
max_length=0
while(true):
max_length = max_length +1
for each program "P" of length <= max_length: # P is finite
for each input "I" of length <= max_length:
if "env" halts on 'I' after max_length steps:
print P,I
Summary
- In order to initialize V(s) to our desired values, we must enumerate all the states
- we can either search the game tree(9!) or find board permutations($3^9$)
- 9! is super-exponential
- Enumerating game states Recursively
- initializing V(s) is different for X and O
6. The Environment Class(Code)
Method: __init__() : #initialize Important instance vars
is_empthy(i,j): # returns true if(i,j) is empty
reward(symbol)
get_state()
game_over()
draw_board()
Constructor
class Environment:
def __init__(self):
self.board = np.zeros((length, length))
self.x = -1 # represents an x on the board, player 1
self.o = 1 # represents an o on the board player 2
self.winner = None
self.ended = False
self.num_states = 3**(length*length)
is_empthy
def is_empthy(self, i, j):
return self.board[i,j] == 0
reward
def reward(self, sym):
# no reward until game is over
if not self.game_over():
return 0
# if we get here, game is over
# sym will be self.x or self.o
return 1 if self.winner == sym else 0
get_state
def get_state(self):
# returns the current state, represented as an int
# from 0...|S|-1, where S = set of all possible states
# |S| = 3^(BOARD SIZE), since each cell can have 3 possible values - empty, x, o
# some states are not possible, e.g. all cells are x, but we ignore that detail
# this is like finding the integer represented by a base-3 number
k = 0
h = 0
for i in range(LENGTH):
for j in range(LENGTH):
if self.board[i,j] == 0:
v = 0
elif self.board[i,j] == self.x:
v = 1
elif self.board[i,j] == self.o:
v = 2
h += (3**k) * v # Value Funtion
k += 1
return h
game_over
def game_over(self, force_recalculate==False):
if not force_recalculate and self.ended:
return self.ended
# check rows
for i in range(LENGTH):
for player in (self.x, self.o):
if self.board[i].sum() == player*LENGTH:
self.winner = player
self.ended = True
return True
# check columns
for j in range(LENGTH):
for player in (self.x, self.o):
if self.board[:,j].sum() == player*LENGTH:
self.winner = player
self.ended = True
return True
# check diagonals
for player in (self.x, self.o):
# top-left -> bottom-right diagonal
if self.board.trace() == player*LENGTH:
self.winner = player
self.ended = True
return True
# top-right -> bottom-left diagonal
if np.fliplr(self.board).trace() == player*LENGTH:
self.winner = player
self.ended = True
return True
# check if draw
if np.all((self.board == 0) == False):
# winner stays None
self.winner = None
self.ended = True
return True
# game is not over
self.winner = None
return False
draw_board
def draw_board(self):
for i in range(LENGTH):
print("-------------")
for j in range(LENGTH):
print(" ", end="")
if self.board[i,j] == self.x:
print("x ", end="")
elif self.board[i,j] == self.o:
print("o ", end="")
else:
print(" ", end="")
print("")
print("-------------")
7. The Agent class
- Contains the AI
- different from supervised/unsupervised ML, because we don’t just feed it data
- it has to interact with the Environment
- one-line update for V(s) is a very small part of the agent, yet responsible for 100% of its intelligence
The Agent Class
class Agent:
def __init__(self, eps=0.1, alpha=0.5):
self.eps = eps # probability of choosing random action instead of greedy
self.alpha = alpha # learning rate
self.verbose = False
self.state_history = []
def setV(self, V): # SetV is the allow us to initialize the value function
self.V = V
def set_symbol(self, sym): # symbol is allow us to give this agent a symbol that it'll use to play on the board
self.sym = sym
def set_verbose(self, v):
# if true, will print values for each position on the board
self.verbose = v
def reset_history(self):
self.state_history = []
Take_action
def take_action(self, env):
# choose an action based on epsilon-greedy strategy
r = np.random.rand()
best_state = None
if r < self.eps:
# take a random action
if self.verbose:
print("Taking a random action")
possible_moves = []
for i in range(LENGTH):
for j in range(LENGTH):
if env.is_empty(i, j):
possible_moves.append((i, j))
idx = np.random.choice(len(possible_moves))
next_move = possible_moves[idx]
else:
# choose the best action based on current values of states
# loop through all possible moves, get their values
# keep track of the best value
pos2value = {} # for debugging
next_move = None
best_value = -1
for i in range(LENGTH):
for j in range(LENGTH):
if env.is_empty(i, j):
# what is the state if we made this move?
env.board[i,j] = self.sym
state = env.get_state()
env.board[i,j] = 0 # don't forget to change it back!
pos2value[(i,j)] = self.V[state]
if self.V[state] > best_value:
best_value = self.V[state]
best_state = state
next_move = (i, j)
# if verbose, draw the board w/ the values
if self.verbose:
print("Taking a greedy action")
for i in range(LENGTH):
print("------------------")
for j in range(LENGTH):
if env.is_empty(i, j):
# print the value
print(" %.2f|" % pos2value[(i,j)], end="")
else:
print(" ", end="")
if env.board[i,j] == env.x:
print("x |", end="")
elif env.board[i,j] == env.o:
print("o |", end="")
else:
print(" |", end="")
print("")
print("------------------")
# make the move
env.board[next_move[0], next_move[1]] = self.sym
update_state_history
def update_state_history(self, s):
# cannot put this in take_action, because take_action only happens
# once every other iteration for each player
# state history needs to be updated every iteration
# s = env.get_state() # don't want to do this twice so pass it in
self.state_history.append(s)
update
def update(self, env):
# we want to BACKTRACK over the states, so that:
# V(prev_state) = V(prev_state) + alpha*(V(next_state) - V(prev_state))
# where V(next_state) = reward if it's the most current state
#
# NOTE: we ONLY do this at the end of an episode
# not so for all the algorithms we will study
reward = env.reward(self.sym)
target = reward
for prev in reversed(self.state_history):
value = self.V[prev] + self.alpha*(target - self.V[prev])
self.V[prev] = value
target = value
self.reset_history()
8. The Human Class(Code)
Human class
class Human:
def __init__(self):
pass
def set_symbol(self, sym):
self.sym = sym
def take_action(self, env):
while True:
# break if we make a legal move
move = input("Enter coordinates i,j for your next move (i,j=0..2): ")
i, j = move.split(',')
i = int(i)
j = int(j)
if env.is_empty(i, j):
env.board[i,j] = self.sym
break
def update(self, env):
pass
def update_state_history(self, s):
pass
# recursive function that will return all
# possible states (as ints) and who the corresponding winner is for those states (if any)
# (i, j) refers to the next cell on the board to permute (we need to try -1, 0, 1)
# impossible games are ignored, i.e. 3x's and 3o's in a row simultaneously
# since that will never happen in a real game
play games
def play_game(p1, p2, env, draw=False):
# loops until the game is over
current_player = None
while not env.game_over():
# alternate between players
# p1 always starts first
if current_player == p1:
current_player = p2
else:
current_player = p1
# draw the board before the user who wants to see it makes a move
if draw:
if draw == 1 and current_player == p1:
env.draw_board()
if draw == 2 and current_player == p2:
env.draw_board()
# current player makes a move
current_player.take_action(env)
# update state histories
state = env.get_state()
p1.update_state_history(state)
p2.update_state_history(state)
if draw:
env.draw_board()
# do the value function update
p1.update(env)
p2.update(env)
Main
if __name__ == '__main__':
# train the agent
p1 = Agent()
p2 = Agent()
# set initial V for p1 and p2
env = Environment()
state_winner_triples = get_state_hash_and_winner(env)
Vx = initialV_x(env, state_winner_triples)
p1.setV(Vx)
Vo = initialV_o(env, state_winner_triples)
p2.setV(Vo)
# give each player their symbol
p1.set_symbol(env.x)
p2.set_symbol(env.o)
T = 10000 #train
for t in range(T):
if t % 200 == 0:
print(t)
play_game(p1, p2, Environment())
# play human vs. agent
# do you think the agent learned to play the game well?
# human Verification
human = Human()
human.set_symbol(env.o)
while True:
p1.set_verbose(True)
play_game(p1, human, Environment(), draw=2)
# I made the agent player 1 because I wanted to see if it would
# select the center as its starting move. If you want the agent
# to go second you can switch the human and AI.
answer = input("Play again? [Y/n]: ")
if answer and answer.lower()[0] == 'n':
break
9. Summary
- Would not be able to increase intelligence by learning from experience
- would not be generalizable to other Environments
- Components of a RL system (Agent, Environment, state, action, reward)
- Episodes, terminal states
- Choosing rewards carefully
- credit assignment(움직임에 따라 승리의 확율을 나타낸다)
- Delayed Reward
- Planning intelligently to maximize overall rewards
- Value function
- V(s) <- V(s) + α(V(s’)- V(s))
RL vs SL
- why not use a supervised learning model that maps states -> actions directly
- i.e model y = f(x) where x = state, y= action
- how would we come up with labels?
- very easy for state space to grow too large to enumerate
- connect-4/ tic-tac-toe is probably the limit
- imagine: HD graphics 60 FPS video game - we can’t even conceptualize how large the state space
- thus, how could we create a label for every state?
- Rewards are delayed(데이터가 없는 상태에서 액션을 즉시 선택하는 것은 올바르지 않기 때문에, 데이터를 쌓은 상태에서 액션을 취하려 Reward Delayed를 한다)
- but in Rl value function has the “future” built into it
- if doing SL, and somehow manage to get around a humongous(巨大的) state-space, how would we choose the right actions?
- instead of letting the value function take care of measuring the future, we need to somehow keep track of what’s best for all future possibilities
- Rewards can have component of randomness. (E.g same state gives reward of 1 or 0 )(E.g2. we study for our exam tomorrow, then there is a snow storm and our exam is canceled)
- Next states can also be random
- In RL, we are never told if a state-action pair is good or not
- the only way we can find out is if we “discover” it ourselves by performing the action
- RL is online. after each episode of tic-tac-toe, we get better
- compare to decision tree - a tree is made based on entire training set
- if we want to incorporate new data, start training all over again
Reference:
Artificial Intelligence Reinforcement Learning



Comments