9. Markov Decision Processes
28 Sep 2019 | Reinforcement Learning
Markov Decision Processes
- this section: formalize some RL concepts we already know about
- Agent, Environment, action, state, reward, episode
- Formal Framework: Markov Decision Processes(MDPs)
1. Typical Game by solving MDPs is GridWord
- possible actions:
- up,down,left,right
- (1,1) -> wall,can’t go here
- (0,3) -> Terminal(+1 Reward)
- (1,3) -> Terminal(-1 Reward)
- 12 Positions(w x h = 3 x 4 = 12)
- 11 states (where the robot is)
- 4 actions
2. Markov Property
- Given a sequence:
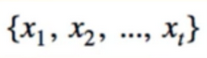
- Generally, this can’t be simplified:
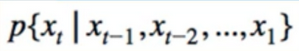
- First-order Markov:
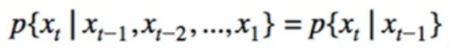
- second-order Markov:

- Simple Example
```
Consider the sentence : “Let’s do a simple example”
Given:”let’s do a simple”
Predict the new word? Easy
Given: “simple”
Predict the next word? not as easy
Given: “a”
predict the next word? very difficult
is the Markov Property limiting? Not necessarily
```
3. Markov Property in RL
- {S(t), A(t)} produces 2 things -> {S(t+1),R(t+1)}
- Markov Property:

- Convenience notation
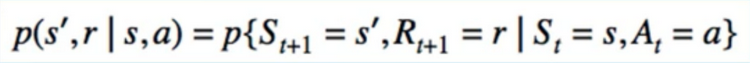
- joint on s’ and r, conditioned on 2 other variables
- different from “usual” Markov: 1 RV(Random Variable) Conditioned on 1 other RV
4. Other Conditional distributions
- can be found using rules of probability
- For pretty much all cases we’ll consider these will be deterministic
- i.e. states will always give us the same reward
- Action will always bring us to same next state
- But, these distributions are part of the core theory of RL
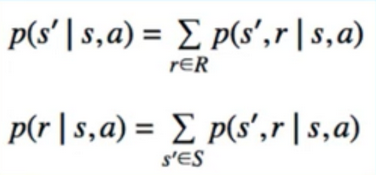
5. Is the Markov Assumption limiting?
- Not necessarily
- Recent application: DeepMind used concatenation(一系列相关联的事物) of 4 most recent frames to represent state when playing Atari Games
- State can be made up of anything from anytime past to current
- Typically think of state right now = something we measure right now
- Also, don’t need to use raw data(state can be features transformed from raw data)
- Any input from agent’s sensors can be used to form state
6. Markov Decision Processes(MDPs)
- Any RL task with a set of States, actions, and rewards, that follows the Markov Property, is a MDP
- MDP is defined as the collection of
- set of states
- set of actions
- set of rewards
- State-Transition probability, Reward probability(as defined jointly(连带地) earlier)
- Discount factor
- Often written as a 5 tuples
7. Policy
- One more piece to complete the puzzle - the policy(denoted by π)
- Technically π is not part of the MDP itself, but it, along with the value function, form the solution
- Left out until now because it’s a weird symbol
- there’s no “equation” for it
- how do we write epsilon-greedy as an equation? it’s more like an algorithm
- the only exception is the Optimal policy, which can be defined in terms of the value function
- think of π as shorthand for the algorithm the agent is using to navigate the environment
8. State-Transition probability - p(s’|s,a)
- State Diagram
- p(s’ I s,a)
- why is this stochastic? if i press “jump” button, doesn’t it always do the same thing?
- Recall: state is only derived from what agent senses, it’s not the environment itself
- State can be imperfect representation of environment
- Ex) state could represent multiple configuration of environment
- Ex) Blackjack - if we’re the agent, the dealer’s next card is not part of our state(but it is part of the environment)
9. Actions vs Environment
- Typically we think of action like joystick inputs(up/down/left/right/jump) or Blackjack Moves(hit/stand)
- Actions can be very board: how to distribute government funding
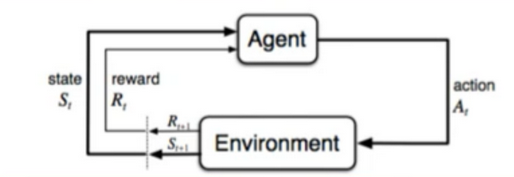
- we are navigating an environment, we are the agent - what constitutes(구성하다) “us”?
- Are our body? No
- our body is part of the environment, our body doesn’t make decisions/learn
- brain/mind does the learning
10. Total Reward & Future Reward
- We are Interested in measuring total future reward
- Everything from t+1 onward(继续的)
- We call this the Return, G(t)
- Note: does not count current reward R(t)
Future Reward
- Imagine a very long task(thousands of steps)
- is there a difference between getting a reward now, and getting the same reward 10 years from now?
- think finance
- $1000 today is worth less than $ 1000 10 years ago
- Would you rather get $1000 today or $1000 10 years from now? choose today
11. Discount Factor
- Gamma = 1: don’t care how far is the future reward is, weight all equally
- Gamma = 0: truly greedy, only try to maximize immediate reward
- Usually we choose something close to 1, i.e 0.9
- Short episode task: maybe don’t discount at all
- “the further we look into the future, the harder it is to predict”
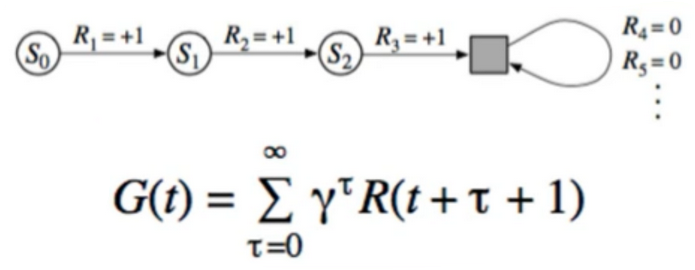
12. Merging Continuous and episode tasks
- why count up to infinity? Aren’t we doing episodic tasks?
- yes, but math is easier with infinity. so can make them technically equivalent(相等的)
번외
- (Epsilon Greedy는 주사위 한번 던져서 결정하고 그 action 다음번에 사용하는 것이 on Policy)
- (Q-Learning은 다음 Step에서 실제로 사용할 action과 상관 없이 Max Q 취하기 때문에 off policy)
- 각 지점에서 계속 최적값을 찾으면서 Future Reward 计算
- 벨멘 방정식을 이용하여 반복적으로 Q함수를 근사시킬 수 있음
- (Sarsa, 다음번에 게임에 넣어줄 action을 미리 계산해서 사용)
- Reinforcement Learning Two Problem
- Credit Assignment Problem
- Exploration-exploitation
- DQN Property
- Target Q function
- 학습 대상이 되는 Q함수가 학습이 되면서 계속 바뀌는 문제
- Learning Q-Fucntion from Gradient Descent
- 일정 스텝 될 때마다 Q 함수의 가중치를 타켓 Q함수에 업데이트
- Replay Memory
- 학습의 재료가 되는 Sample 저장소
- 즉시 훈련하지 않고, 메로리 저장
- 일정 수의 Samplr을 랜덤으로 꺼내 학습
- Q-function made by ANN
- DQN은 인공신경망으로 Policy function을 Approximate
- Q function of DQN 특징
- Model Free :
- 모델이 없고 샘플로 부터 직접적으로 정책을 근사화
- 대부분 ANN을 활용한 훈련으로 Dimension Curse에 벗어난다.
- Off-Policy
- Learn thing from another agent’s action
- 타겟 정책과 행동 정책 나눈다.
- Target policy : 우리가 강화학습 에이전트에게 가르치기 위한 기준이 되는 정책
- 행동 Policy : 탐험을 하며 새로운 행동을 만들어 내는 정책
- 두가지 폴리시를 다루어야 함으로 구현하기 어려움
- MiniBatch
- 많은 데이터 중 임의로 샘플을 뽑아 학습시키는 것
- 연속적인 샘플들 간의 강한 상관관계를 제거
- Value-Based Reinforcement Learning
- at first, Let Value Function Approximating to make a Policy
- Decaying Epsilon-Greedy
- at first, Random Act -> random act to be reduced gradually -> when it became 1% of random action, it stop
- Two Hyper parameter:
(1) Exploration_fraction : 언제까지 감소 시킬 것인가? Default 0.5(Timesteps의 50%가 될 때까지 랜덤 액션 취할 확률 이 줄어든다)
(2) Exploration_final_eps : 최종 입실론 값, 기본값 0.01(0.01이 되면 감소가 줄어들고, 값을 유지한다.)
Reference:
Artificial Intelligence Reinforcement Learning
Markov Decision Processes
- this section: formalize some RL concepts we already know about
- Agent, Environment, action, state, reward, episode
- Formal Framework: Markov Decision Processes(MDPs)
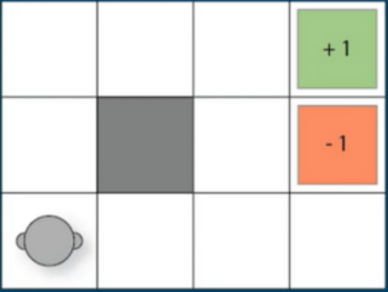
1. Typical Game by solving MDPs is GridWord
- possible actions:
- up,down,left,right
- (1,1) -> wall,can’t go here
- (0,3) -> Terminal(+1 Reward)
- (1,3) -> Terminal(-1 Reward)
- 12 Positions(w x h = 3 x 4 = 12)
- 11 states (where the robot is)
- 4 actions
2. Markov Property
- Given a sequence:
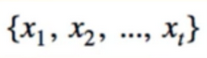
- Generally, this can’t be simplified:
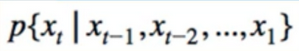
- First-order Markov:
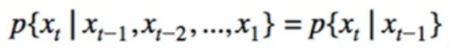
- second-order Markov:

- Simple Example ``` Consider the sentence : “Let’s do a simple example” Given:”let’s do a simple” Predict the new word? Easy
Given: “simple” Predict the next word? not as easy
Given: “a” predict the next word? very difficult
is the Markov Property limiting? Not necessarily ```
3. Markov Property in RL
- {S(t), A(t)} produces 2 things -> {S(t+1),R(t+1)}
- Markov Property:

- Convenience notation
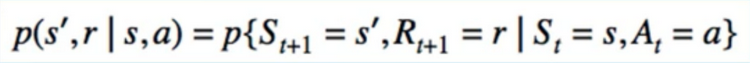
- joint on s’ and r, conditioned on 2 other variables
- different from “usual” Markov: 1 RV(Random Variable) Conditioned on 1 other RV
4. Other Conditional distributions
- can be found using rules of probability
- For pretty much all cases we’ll consider these will be deterministic
- i.e. states will always give us the same reward
- Action will always bring us to same next state
- But, these distributions are part of the core theory of RL
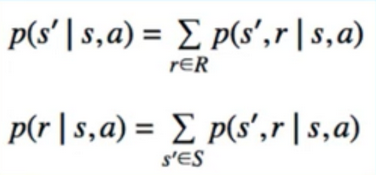
5. Is the Markov Assumption limiting?
- Not necessarily
- Recent application: DeepMind used concatenation(一系列相关联的事物) of 4 most recent frames to represent state when playing Atari Games
- State can be made up of anything from anytime past to current
- Typically think of state right now = something we measure right now
- Also, don’t need to use raw data(state can be features transformed from raw data)
- Any input from agent’s sensors can be used to form state
6. Markov Decision Processes(MDPs)
- Any RL task with a set of States, actions, and rewards, that follows the Markov Property, is a MDP
- MDP is defined as the collection of
- set of states
- set of actions
- set of rewards
- State-Transition probability, Reward probability(as defined jointly(连带地) earlier)
- Discount factor
- Often written as a 5 tuples
7. Policy
- One more piece to complete the puzzle - the policy(denoted by π)
- Technically π is not part of the MDP itself, but it, along with the value function, form the solution
- Left out until now because it’s a weird symbol
- there’s no “equation” for it
- how do we write epsilon-greedy as an equation? it’s more like an algorithm
- the only exception is the Optimal policy, which can be defined in terms of the value function
- think of π as shorthand for the algorithm the agent is using to navigate the environment
8. State-Transition probability - p(s’|s,a)
- State Diagram
- p(s’ I s,a)
- why is this stochastic? if i press “jump” button, doesn’t it always do the same thing?
- Recall: state is only derived from what agent senses, it’s not the environment itself
- State can be imperfect representation of environment
- Ex) state could represent multiple configuration of environment
- Ex) Blackjack - if we’re the agent, the dealer’s next card is not part of our state(but it is part of the environment)
9. Actions vs Environment
- Typically we think of action like joystick inputs(up/down/left/right/jump) or Blackjack Moves(hit/stand)
- Actions can be very board: how to distribute government funding

- we are navigating an environment, we are the agent - what constitutes(구성하다) “us”?
- Are our body? No
- our body is part of the environment, our body doesn’t make decisions/learn
- brain/mind does the learning
10. Total Reward & Future Reward
- We are Interested in measuring total future reward
- Everything from t+1 onward(继续的)
- We call this the Return, G(t)
- Note: does not count current reward R(t)
Future Reward
- Imagine a very long task(thousands of steps)
- is there a difference between getting a reward now, and getting the same reward 10 years from now?
- think finance
- $1000 today is worth less than $ 1000 10 years ago
- Would you rather get $1000 today or $1000 10 years from now? choose today
11. Discount Factor
- Gamma = 1: don’t care how far is the future reward is, weight all equally
- Gamma = 0: truly greedy, only try to maximize immediate reward
- Usually we choose something close to 1, i.e 0.9
- Short episode task: maybe don’t discount at all
- “the further we look into the future, the harder it is to predict”
12. Merging Continuous and episode tasks
- why count up to infinity? Aren’t we doing episodic tasks?
- yes, but math is easier with infinity. so can make them technically equivalent(相等的)
번외
- (Epsilon Greedy는 주사위 한번 던져서 결정하고 그 action 다음번에 사용하는 것이 on Policy)
- (Q-Learning은 다음 Step에서 실제로 사용할 action과 상관 없이 Max Q 취하기 때문에 off policy)
- 각 지점에서 계속 최적값을 찾으면서 Future Reward 计算
- 벨멘 방정식을 이용하여 반복적으로 Q함수를 근사시킬 수 있음
- (Sarsa, 다음번에 게임에 넣어줄 action을 미리 계산해서 사용)
- Reinforcement Learning Two Problem
- Credit Assignment Problem
- Exploration-exploitation
- DQN Property
- Target Q function
- 학습 대상이 되는 Q함수가 학습이 되면서 계속 바뀌는 문제
- Learning Q-Fucntion from Gradient Descent
- 일정 스텝 될 때마다 Q 함수의 가중치를 타켓 Q함수에 업데이트
- Replay Memory
- 학습의 재료가 되는 Sample 저장소
- 즉시 훈련하지 않고, 메로리 저장
- 일정 수의 Samplr을 랜덤으로 꺼내 학습
- Q-function made by ANN
- DQN은 인공신경망으로 Policy function을 Approximate
- Q function of DQN 특징
- Model Free :
- 모델이 없고 샘플로 부터 직접적으로 정책을 근사화
- 대부분 ANN을 활용한 훈련으로 Dimension Curse에 벗어난다.
- Off-Policy
- Learn thing from another agent’s action
- 타겟 정책과 행동 정책 나눈다.
- Target policy : 우리가 강화학습 에이전트에게 가르치기 위한 기준이 되는 정책
- 행동 Policy : 탐험을 하며 새로운 행동을 만들어 내는 정책 - 두가지 폴리시를 다루어야 함으로 구현하기 어려움
- MiniBatch
- 많은 데이터 중 임의로 샘플을 뽑아 학습시키는 것
- 연속적인 샘플들 간의 강한 상관관계를 제거
- Value-Based Reinforcement Learning
- at first, Let Value Function Approximating to make a Policy
- Decaying Epsilon-Greedy
- at first, Random Act -> random act to be reduced gradually -> when it became 1% of random action, it stop
- Two Hyper parameter: (1) Exploration_fraction : 언제까지 감소 시킬 것인가? Default 0.5(Timesteps의 50%가 될 때까지 랜덤 액션 취할 확률 이 줄어든다) (2) Exploration_final_eps : 최종 입실론 값, 기본값 0.01(0.01이 되면 감소가 줄어들고, 값을 유지한다.)
Reference:
Artificial Intelligence Reinforcement Learning
- Model Free :
- Target Q function

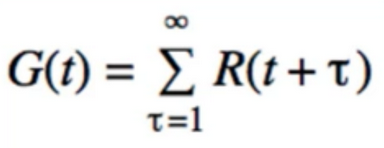
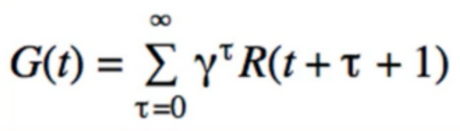
Comments