11. Introduction to Dynamic Programming
29 Sep 2019 | Reinforcement Learning
intro to Dynamic Programming
- Solutions to MDPs
- Centrepiece of MDP: The bellman Equation

- if we look carefully, this can be used to solve for V(s) Directly
- I S I equations, I S I unknowns(linear Problem)
- Many entries(进入(指行动)) will be 0, since transitions s -> s’ are sparse
- Instead, we will use Iterative Policy evaluation
1. Iterative Policy evaluation
def iterative_policy_evaluation(π):
initialize V(s) = 0 for all s ∈ S
while true :
∆ = 0
for each s ∈ S:
old_v = V(s)
∆ = max(∆, I V(s) - old_v I )
if ∆ < Threshold: break
return V(s)
- Technically, it’s defined where V(s) at iteration k+1 is updated from V(s) at iteration k
- But we can update V(s) “in place”, to use the most recently updated values
- Converges(汇集) Faster
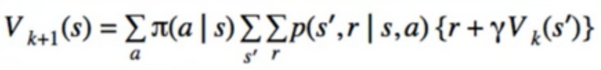
Definition
- What we just did(Finding V(s) given a policy) is called the Prediction Problem
- Finding the optimal policy is called the Control Problem
2. Designing our RL Program
- Let’s recap how to do this in supervised learning
class MyModel;
def fit(x,y):
# our job
def predict(x)
# our job
# boilerplate
Xtrain, Ytrain, Xtest, Ytest = get_data() # 1. Get Data
Model = MyModel() # 2. Instantiate Model
model.fit(Xtrain,Ytrain) # 3. Train Model
model.score(Xtest, ytest) # 4. Evaluation Model
- RL Program is not supervised learning but there is still a pattern to be followed
- Same as bandit section: several algorithms, but all have the same interface
- Only the algorithm is different, not the layout
- Applies to all the RL algorithms
- Designing our RL Program, there are t types of problems
- Prediction Problem: Given a policy, find V(s)
- Goal: Find V(s)
given: policy
V(s) = initial value
for t in range(max_iterations):
states, actions, rewards = play_game(policy)
update V(s) given (state, actions, rewards)
print useful info (change in V(s) vs time, final V(s), policy)
2. Control Problem : Find the optimal policy and the corresponding value function
- Goal : find the optimal Policy
- note : Policy may not be explicitly represented
initialize value function and Policy
for t in range(max_iterations):
states, actions, rewards = play_game(policy)
update Value function and policy to (states, actions,rewards) using the algorithm
print useful info (change in V(s) vs time, final V(s), final policy)
3. Iterative Policy Evaluation
- we will look at 2 different Policies
- First: Completely random(Uniform) policy
- which is relavant?
- π(a I s)
- p(s’,r I s,a)
- Answer : π(a I s)
- for a uniformly random policy, this will be 1/IA(s)I
- A(s) = set of possible actions from state s
-
p(s’,r I s,a) is only relevant when state transitions are random
- Second: policy we we’ll look at is Completely deterministic
- from start position, we go Directly to goal
- otherwise, we go Directly to losing state
4. Policy Improvement
- THe control Problem
- How to find better policies -> optimal policy
- what we know so far : how to find V/Q given a fixed policy

- using the current policy, we simply get the state-value function
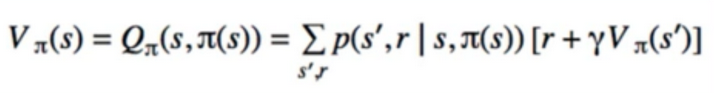
- can we change just this one action for s? i.e. choose a != π(s)
- Yes
- we have a finite set of actions, so just go through each one until we get a better Q
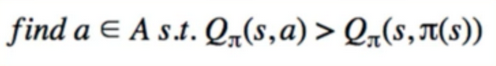
- this looks complicated, but it’s very simple
- all it’s saying is, if the policy for state s is to currently go “up”
- just check “left”, “right”, and “down” to see if we can get a bigger Q
- if so, change our policy for state s to the new action
- Formally, we’re finding a new policy π’, that gives us a givver value than we had before:
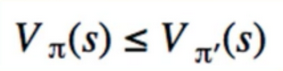
- if we have Q:

- if we have V:
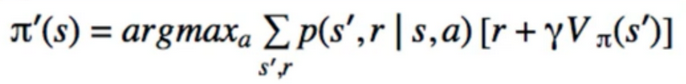
- Notice : it’s greedy
- we never consider globally the value function at all states
- only look at current state s
- notice: it uses an imperfect version of $V_π$(s)
- once we change π. $V_π$(s) also changes
- when are we finished changing the policy, it doesn’t change when we try policy Improvement, V(s) also doesn’t change
- ”<” when still improving = when finished
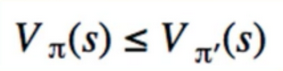
- if we found optimal policy, Value function is always same in state
5. Policy Iteration
- this is what use to find the optimal policy
- problem we encountered last lecture: when we change the policy, the value function becomes out of date
- How do we fix the out-of-date value function?
- simply recalculate it given the new policy
- we already know how to find V given π:
- iterative policy Evaluation
- High-level: alternate between policy evaluation and policy improvement
- keep doing this until policy doesn’t change
- Don’t need to check value function for convergence, because once policy becomes constant so will value
Step of Policy Iteration
- Randomly initialize V(s) and the policy π(s)
- V(s) = iterative_policy_evaluation(π)
- algorithm
policy_changed = False
for s in all_state:
old_a = policy(s)
policy(s) = argmax[a]{sum[s',r]{p(s',r I s, a )[ r+ gamma*V(s')]}}
if policy(s) != old_a: policy_changed = true
if policy_changed: go back to step 2
6. Example (Windy Gridworld)
- recall, we have 2 probability distributions to deal with:
- π(a I s)
- p(s’,r I s,a)
- so far, p(s’,r I s,a) has been deterministic
- in windy Gridworld, it’s not
- imagine we are walking on a windy street. we try to walk straight but wind push we back or left.
- same thins in windy Gridworld
- if agent tries to go “up”, it will do so with probability 0.5
- But it can also go “left”, “down”, or “right” with probability 0.5/3
code
# https://deeplearningcourses.com/c/artificial-intelligence-reinforcement-learning-in-python
# https://www.udemy.com/artificial-intelligence-reinforcement-learning-in-python
from __future__ import print_function, division
from builtins import range
# Note: you may need to update your version of future
# sudo pip install -U future
import numpy as np
from grid_world import standard_grid, negative_grid
from iterative_policy_evaluation import print_values, print_policy
SMALL_ENOUGH = 1e-3
GAMMA = 0.9
ALL_POSSIBLE_ACTIONS = ('U', 'D', 'L', 'R')
# next state and reward will now have some randomness
# you'll go in your desired direction with probability 0.5
# you'll go in a random direction a' != a with probability 0.5/3
if __name__ == '__main__':
# this grid gives you a reward of -0.1 for every non-terminal state
# we want to see if this will encourage finding a shorter path to the goal
grid = negative_grid(step_cost=-1.0)
# what is the step_cost? for example, if we are three steps away from the goal
# we get minus three reward before we even have a chance to get to the goal
# if we are only one step away from the losing state, then we only get minus one reward
# grid = negative_grid(step_cost=-0.1)
# grid = standard_grid()
# print rewards
print("rewards:")
print_values(grid.rewards, grid)
# state -> action
# we'll randomly choose an action and update as we learn
policy = {}
for s in grid.actions.keys():
policy[s] = np.random.choice(ALL_POSSIBLE_ACTIONS)
# initial policy
print("initial policy:")
print_policy(policy, grid)
# initialize V(s)
V = {}
states = grid.all_states()
for s in states:
# V[s] = 0
if s in grid.actions:
V[s] = np.random.random()
else:
# terminal state
V[s] = 0
# repeat until convergence - will break out when policy does not change
while True:
# policy evaluation step - we already know how to do this!
while True:
biggest_change = 0
for s in states:
old_v = V[s]
# print(old_v)
# V(s) only has value if it's not a terminal state
new_v = 0
if s in policy:
for a in ALL_POSSIBLE_ACTIONS:
if a == policy[s]:
p = 0.5
else:
p = 0.5/3
grid.set_state(s)
r = grid.move(a)
new_v += p*(r + GAMMA * V[grid.current_state()])
V[s] = new_v
biggest_change = max(biggest_change, np.abs(old_v - V[s]))
if biggest_change < SMALL_ENOUGH:
break
# policy improvement step
is_policy_converged = True
for s in states:
if s in policy:
old_a = policy[s]
new_a = None
best_value = float('-inf')
# loop through all possible actions to find the best current action
for a in ALL_POSSIBLE_ACTIONS: # chosen action
v = 0
for a2 in ALL_POSSIBLE_ACTIONS: # resulting action
if a == a2:
p = 0.5
else:
p = 0.5/3
grid.set_state(s)
r = grid.move(a2)
v += p*(r + GAMMA * V[grid.current_state()])
if v > best_value:
best_value = v
new_a = a
policy[s] = new_a
if new_a != old_a:
is_policy_converged = False
if is_policy_converged:
break
print("values:")
print_values(V, grid)
print("policy:")
print_policy(policy, grid)
# result: every move is as bad as losing, so lose as quickly as possible
6. Value Iteration
- Alternative technique for solving the control Problem called value iteration
- Previous technique: policy Iteration
- Disadvantage of policy iteration:
- iterative algorithm
- inside another iterative algorithm
- Value Iteration is that Policy evaluation step ends when V coverages
- is there a point before V Converges, s.t the resulting greedy policy wouldn’t change?
- Yes
- therefore, we don’t need to wait for policy evaluation to finish. just do a few steps
- because the policy improvement step will find the same policy anyway
- Value iteration takes this one step further
- it combines policy evaluation and policy improvement into one step:
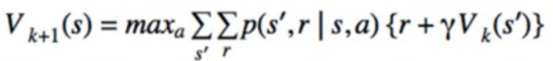
- what is the difference? taking the max over all possible action
- Iterative, but don’t need to wait for (k)th iteration of V finish before calculating (k+1)th
- just update it “in-place(在正确的位置)” as before
- since policy improvement uses argmax, by taking the max, we’re just doing the next policy evaluation step without calculating policy explicitly


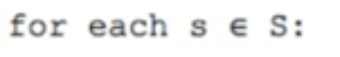
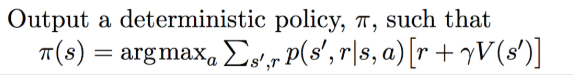
7. Summary
- Last section : Defined Markov Decision Process
- This section : one method for finding solutions to MDP: Dynamic Programming
- Prediction Problem: Iterative Policy evaluation
- Control Problem: Policy iteration, Value iteration
- finding the optimal policy and optimal value function
Asynchronous(不同时存在) Dynamic Programming
- Every DP algorithm we looked at involved looping through entire set of states
- Recall that for many realistic games, state space is ridiculously large
- thus, even one iteration can take a long time
- one way to speed up: update V(s) “in-place”
- we can take that one step further: Asynchronous(不同时存在) Dynamic Programming
- instead of looping through all states, loop through a few or only one
- Choose based one which states are most-visited
- can be learned by playing the game
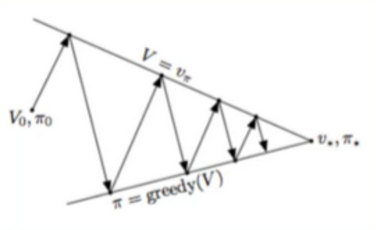
Generalized Policy iteration
- Main concept behind policy iteration: we iteratively alternate between 2 steps - policy evaluation and policy improvement
- Converge when bellman’s equation becomes true(i.e. V(s) = right-hand side)
Efficiency of DP
- Consider how long it would take to do brute force search
- . # States = N, # actions = M
- if we assume we can go from start to goal state in O(N) time, then we want to explore action sequences of length O(N)
- M x M x … x M
- we did this problem earlier in tic-tac-toe section
-
of possible permutation(排列(方式)) is O(M^n)
- Once we generate all possible sequences, do policy evaluation on all to find the best V(s)
- exponential in # of states
Model-based vs Model-free
- Notice how DP requires full model of the environment
- In Particular, p(s’,r I s,a)
- In the real world, these may be hard to measuring, especially if ISI is large
- next sections will look at methods which don’t require such a model - called model-free methods
- also notice there iterative methods requires an initial estimate
- we make estimates from other estimates (V(s) and policy )
- Making an initial estimate is called Bootstrapping
- Monte Carlo (MC) Does not require boot Bootstrapping
- Temporal difference(TD) learning does
Reference:
Artificial Intelligence Reinforcement Learning
intro to Dynamic Programming
- Solutions to MDPs
- Centrepiece of MDP: The bellman Equation

- if we look carefully, this can be used to solve for V(s) Directly
- I S I equations, I S I unknowns(linear Problem)
- Many entries(进入(指行动)) will be 0, since transitions s -> s’ are sparse
- Instead, we will use Iterative Policy evaluation
1. Iterative Policy evaluation
def iterative_policy_evaluation(π):
initialize V(s) = 0 for all s ∈ S
while true :
∆ = 0
for each s ∈ S:
old_v = V(s)
∆ = max(∆, I V(s) - old_v I )
if ∆ < Threshold: break
return V(s)
- Technically, it’s defined where V(s) at iteration k+1 is updated from V(s) at iteration k
- But we can update V(s) “in place”, to use the most recently updated values
- Converges(汇集) Faster
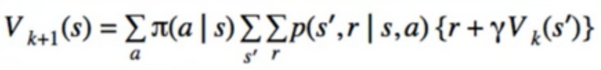
Definition
- What we just did(Finding V(s) given a policy) is called the Prediction Problem
- Finding the optimal policy is called the Control Problem
2. Designing our RL Program
- Let’s recap how to do this in supervised learning
class MyModel;
def fit(x,y):
# our job
def predict(x)
# our job
# boilerplate
Xtrain, Ytrain, Xtest, Ytest = get_data() # 1. Get Data
Model = MyModel() # 2. Instantiate Model
model.fit(Xtrain,Ytrain) # 3. Train Model
model.score(Xtest, ytest) # 4. Evaluation Model
- RL Program is not supervised learning but there is still a pattern to be followed
- Same as bandit section: several algorithms, but all have the same interface
- Only the algorithm is different, not the layout
- Applies to all the RL algorithms
- Designing our RL Program, there are t types of problems
- Prediction Problem: Given a policy, find V(s)
- Goal: Find V(s)
given: policy V(s) = initial value for t in range(max_iterations): states, actions, rewards = play_game(policy) update V(s) given (state, actions, rewards) print useful info (change in V(s) vs time, final V(s), policy)2. Control Problem : Find the optimal policy and the corresponding value function - Goal : find the optimal Policy
- note : Policy may not be explicitly represented
initialize value function and Policy for t in range(max_iterations): states, actions, rewards = play_game(policy) update Value function and policy to (states, actions,rewards) using the algorithm print useful info (change in V(s) vs time, final V(s), final policy)
3. Iterative Policy Evaluation
- we will look at 2 different Policies
- First: Completely random(Uniform) policy
- which is relavant?
- π(a I s)
- p(s’,r I s,a)
- Answer : π(a I s)
- for a uniformly random policy, this will be 1/IA(s)I
- A(s) = set of possible actions from state s
-
p(s’,r I s,a) is only relevant when state transitions are random
- Second: policy we we’ll look at is Completely deterministic
- from start position, we go Directly to goal
- otherwise, we go Directly to losing state
4. Policy Improvement
- THe control Problem
- How to find better policies -> optimal policy
- what we know so far : how to find V/Q given a fixed policy

- using the current policy, we simply get the state-value function
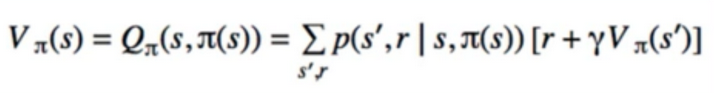
- can we change just this one action for s? i.e. choose a != π(s)
- Yes
- we have a finite set of actions, so just go through each one until we get a better Q
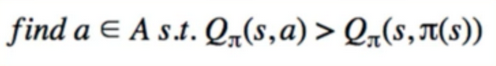
- this looks complicated, but it’s very simple
- all it’s saying is, if the policy for state s is to currently go “up”
- just check “left”, “right”, and “down” to see if we can get a bigger Q
- if so, change our policy for state s to the new action
- Formally, we’re finding a new policy π’, that gives us a givver value than we had before:
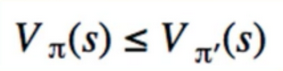
- if we have Q:

- if we have V:
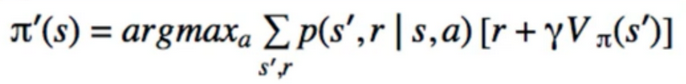
- Notice : it’s greedy
- we never consider globally the value function at all states
- only look at current state s
- notice: it uses an imperfect version of $V_π$(s)
- once we change π. $V_π$(s) also changes
- when are we finished changing the policy, it doesn’t change when we try policy Improvement, V(s) also doesn’t change
- ”<” when still improving = when finished
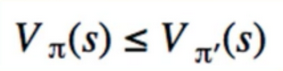
- if we found optimal policy, Value function is always same in state
5. Policy Iteration
- this is what use to find the optimal policy
- problem we encountered last lecture: when we change the policy, the value function becomes out of date
- How do we fix the out-of-date value function?
- simply recalculate it given the new policy
- we already know how to find V given π:
- iterative policy Evaluation
- High-level: alternate between policy evaluation and policy improvement
- keep doing this until policy doesn’t change
- Don’t need to check value function for convergence, because once policy becomes constant so will value
Step of Policy Iteration
- Randomly initialize V(s) and the policy π(s)
- V(s) = iterative_policy_evaluation(π)
- algorithm
policy_changed = False
for s in all_state:
old_a = policy(s)
policy(s) = argmax[a]{sum[s',r]{p(s',r I s, a )[ r+ gamma*V(s')]}}
if policy(s) != old_a: policy_changed = true
if policy_changed: go back to step 2
6. Example (Windy Gridworld)
- recall, we have 2 probability distributions to deal with:
- π(a I s)
- p(s’,r I s,a)
- so far, p(s’,r I s,a) has been deterministic
- in windy Gridworld, it’s not
- imagine we are walking on a windy street. we try to walk straight but wind push we back or left.
- same thins in windy Gridworld
- if agent tries to go “up”, it will do so with probability 0.5
- But it can also go “left”, “down”, or “right” with probability 0.5/3
code
# https://deeplearningcourses.com/c/artificial-intelligence-reinforcement-learning-in-python
# https://www.udemy.com/artificial-intelligence-reinforcement-learning-in-python
from __future__ import print_function, division
from builtins import range
# Note: you may need to update your version of future
# sudo pip install -U future
import numpy as np
from grid_world import standard_grid, negative_grid
from iterative_policy_evaluation import print_values, print_policy
SMALL_ENOUGH = 1e-3
GAMMA = 0.9
ALL_POSSIBLE_ACTIONS = ('U', 'D', 'L', 'R')
# next state and reward will now have some randomness
# you'll go in your desired direction with probability 0.5
# you'll go in a random direction a' != a with probability 0.5/3
if __name__ == '__main__':
# this grid gives you a reward of -0.1 for every non-terminal state
# we want to see if this will encourage finding a shorter path to the goal
grid = negative_grid(step_cost=-1.0)
# what is the step_cost? for example, if we are three steps away from the goal
# we get minus three reward before we even have a chance to get to the goal
# if we are only one step away from the losing state, then we only get minus one reward
# grid = negative_grid(step_cost=-0.1)
# grid = standard_grid()
# print rewards
print("rewards:")
print_values(grid.rewards, grid)
# state -> action
# we'll randomly choose an action and update as we learn
policy = {}
for s in grid.actions.keys():
policy[s] = np.random.choice(ALL_POSSIBLE_ACTIONS)
# initial policy
print("initial policy:")
print_policy(policy, grid)
# initialize V(s)
V = {}
states = grid.all_states()
for s in states:
# V[s] = 0
if s in grid.actions:
V[s] = np.random.random()
else:
# terminal state
V[s] = 0
# repeat until convergence - will break out when policy does not change
while True:
# policy evaluation step - we already know how to do this!
while True:
biggest_change = 0
for s in states:
old_v = V[s]
# print(old_v)
# V(s) only has value if it's not a terminal state
new_v = 0
if s in policy:
for a in ALL_POSSIBLE_ACTIONS:
if a == policy[s]:
p = 0.5
else:
p = 0.5/3
grid.set_state(s)
r = grid.move(a)
new_v += p*(r + GAMMA * V[grid.current_state()])
V[s] = new_v
biggest_change = max(biggest_change, np.abs(old_v - V[s]))
if biggest_change < SMALL_ENOUGH:
break
# policy improvement step
is_policy_converged = True
for s in states:
if s in policy:
old_a = policy[s]
new_a = None
best_value = float('-inf')
# loop through all possible actions to find the best current action
for a in ALL_POSSIBLE_ACTIONS: # chosen action
v = 0
for a2 in ALL_POSSIBLE_ACTIONS: # resulting action
if a == a2:
p = 0.5
else:
p = 0.5/3
grid.set_state(s)
r = grid.move(a2)
v += p*(r + GAMMA * V[grid.current_state()])
if v > best_value:
best_value = v
new_a = a
policy[s] = new_a
if new_a != old_a:
is_policy_converged = False
if is_policy_converged:
break
print("values:")
print_values(V, grid)
print("policy:")
print_policy(policy, grid)
# result: every move is as bad as losing, so lose as quickly as possible
6. Value Iteration
- Alternative technique for solving the control Problem called value iteration
- Previous technique: policy Iteration
- Disadvantage of policy iteration:
- iterative algorithm
- inside another iterative algorithm
- iterative algorithm
- Value Iteration is that Policy evaluation step ends when V coverages
- is there a point before V Converges, s.t the resulting greedy policy wouldn’t change?
- Yes
- therefore, we don’t need to wait for policy evaluation to finish. just do a few steps
- because the policy improvement step will find the same policy anyway
- Value iteration takes this one step further
- it combines policy evaluation and policy improvement into one step:
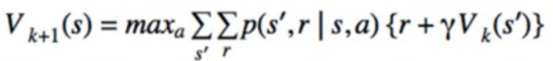
- what is the difference? taking the max over all possible action
- Iterative, but don’t need to wait for (k)th iteration of V finish before calculating (k+1)th
- just update it “in-place(在正确的位置)” as before
- since policy improvement uses argmax, by taking the max, we’re just doing the next policy evaluation step without calculating policy explicitly


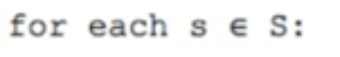
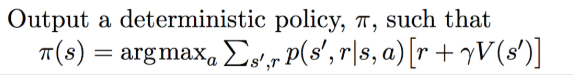
7. Summary
- Last section : Defined Markov Decision Process
- This section : one method for finding solutions to MDP: Dynamic Programming
- Prediction Problem: Iterative Policy evaluation
- Control Problem: Policy iteration, Value iteration
- finding the optimal policy and optimal value function
Asynchronous(不同时存在) Dynamic Programming
- Every DP algorithm we looked at involved looping through entire set of states
- Recall that for many realistic games, state space is ridiculously large
- thus, even one iteration can take a long time
- one way to speed up: update V(s) “in-place”
- we can take that one step further: Asynchronous(不同时存在) Dynamic Programming
- instead of looping through all states, loop through a few or only one
- Choose based one which states are most-visited
- can be learned by playing the game
Generalized Policy iteration
- Main concept behind policy iteration: we iteratively alternate between 2 steps - policy evaluation and policy improvement
- Converge when bellman’s equation becomes true(i.e. V(s) = right-hand side)

Efficiency of DP
- Consider how long it would take to do brute force search
- . # States = N, # actions = M
- if we assume we can go from start to goal state in O(N) time, then we want to explore action sequences of length O(N)
- M x M x … x M
- we did this problem earlier in tic-tac-toe section
-
of possible permutation(排列(方式)) is O(M^n)
- Once we generate all possible sequences, do policy evaluation on all to find the best V(s)
- exponential in # of states
Model-based vs Model-free
- Notice how DP requires full model of the environment
- In Particular, p(s’,r I s,a)
- In the real world, these may be hard to measuring, especially if ISI is large
- next sections will look at methods which don’t require such a model - called model-free methods
- also notice there iterative methods requires an initial estimate
- we make estimates from other estimates (V(s) and policy )
- Making an initial estimate is called Bootstrapping
- Monte Carlo (MC) Does not require boot Bootstrapping
- Temporal difference(TD) learning does
Reference:
Artificial Intelligence Reinforcement Learning

Comments