12. Monte Carlo Methods
29 Sep 2019 | Reinforcement Learning
Montel Carlo(MC) Methods Introduction
- Last Section: Dynamic Programming
- would that work for self-driving cars or video games?
- can i just set the state of the agent?
- “god-mode” capabilities?
- MC Methods learn purely from experience
- Montel Carlo usually refers to any method with a significant random component
- Random Component in RL is the return
- With MC, instead of calculating the true expected value of G, we calculate its sample mean
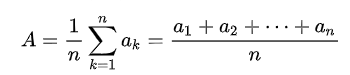
- Need to assume episode tasks only
- Episode must terminate before we calculate return
- Not “fully” online since we need to wait for entire episode to finish before updating
- (full online mean is update after every action)
- monte carlo methods is not fully online which mean it is updated after episode to finish
- Should Remind you of multi-armed bandit
- Multi-Armed bandit : average reward after every action
- MDPs: average the return
- One way to think of MC-MDP is every state is a separate multi-armed bandit problem
- Follow the same pattern
- Prediction Problem(Finding Value given policy)
- Control Problem(finding optimal policy)
1. Monte Carlo for prediction Problem
How do we generate G?
- just play a bunch of episode, log the states and reward sequences
s1 s2 s3 ... sT
r1 r2 r3 ... rT
-
Calculate G from Definition:
G(t) = r(t+1)+gamma*G(t+1)
- very helpful to calculate G by iterating through states in reverse order
- Once we have(s,G) pairs, average them for each s
Multiple Visits to s
- what if we see the same state more than once in an episode
- E.g. we see s at t=1 and t=3
- which return should we use? G(1) or G(3
- First-visit method :
- Use t = 1 only
- Every-visit method :
- Use both t=1 and t=3 as samples
- Surprisingly, it has been proven that both lead to same answer
First-Visit MC Pseudocode
def first_visit_monte_carlo_prediction(π, N):
V = random initialization
all_return = {} # default = []
do N times:
states, returns = play_episode
for s, g in zip(states, returns):
if not seen s in this episode yet:
all_return[s].append(g)
V(s) = sample_mean(all_returns[s])
return V
Sample Mean
- Notice how we store all returns in a list
- Didn’t we discuss how that’s inefficient?
- Can also use previous mean to calculate current mean
- Can also use moving average for non-stationary problems
- Everything we learned before still applies
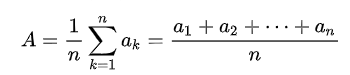
- Rules of probability still apply
- Central limit Theorem
- Variance of estimate = Variance of RV(Random Value) / N
Calculating Returns from Rewards
s = grid.current_state()
states_and_rewards = [(s,0)]
while not game_over:
a = policy(s)
r = grid.move(a)
s = grid.current_state()
states_and_rewards.append((s,r))
G = 0
states_and_returns = []
for s,r in reverse(states_and_rewards):
states_and_returns.((s,G))
G = r + gamma*G
states_and_returns.reverse
MC
- Recall: one Disadvantage of DP is that we need to loop through all states
- MC: only update V for visited states
- We don’t even need to know what all the states are, we can just discover them as we play
2. MC for Windy Gridworld
- Windy Gridworld, different policy
- Policy/transitions were deterministic, MC not really needed
- in windy gridworld, p(s’r I s,a) not deterministic
- with this policy, we try to get to goal
- Values can be -ve, if overall wind pushes us to losing state more often
code
# https://deeplearningcourses.com/c/artificial-intelligence-reinforcement-learning-in-python
# https://www.udemy.com/artificial-intelligence-reinforcement-learning-in-python
from __future__ import print_function, division
from builtins import range
# Note: you may need to update your version of future
# sudo pip install -U future
import numpy as np
from grid_world import standard_grid, negative_grid
from iterative_policy_evaluation import print_values, print_policy
SMALL_ENOUGH = 1e-3
GAMMA = 0.9
ALL_POSSIBLE_ACTIONS = ('U', 'D', 'L', 'R')
# NOTE: this is only policy evaluation, not optimization
def random_action(a):
# choose given a with probability 0.5
# choose some other a' != a with probability 0.5/3
p = np.random.random()
if p < 0.5:
return a
else:
tmp = list(ALL_POSSIBLE_ACTIONS)
tmp.remove(a)
return np.random.choice(tmp)
def play_game(grid, policy):
# returns a list of states and corresponding returns
# reset game to start at a random position
# we need to do this, because given our current deterministic policy
# we would never end up at certain states, but we still want to measure their value
start_states = list(grid.actions.keys())
start_idx = np.random.choice(len(start_states))
grid.set_state(start_states[start_idx])
# random start
s = grid.current_state()
states_and_rewards = [(s, 0)] # list of tuples of (state, reward)
while not grid.game_over():
a = policy[s]
a = random_action(a)
r = grid.move(a)
s = grid.current_state()
states_and_rewards.append((s, r))
# calculate the returns by working backwards from the terminal state
G = 0
states_and_returns = []
first = True
for s, r in reversed(states_and_rewards):
# the value of the terminal state is 0 by definition
# we should ignore the first state we encounter
# and ignore the last G, which is meaningless since it doesn't correspond to any move
if first:
first = False
else:
states_and_returns.append((s, G))
G = r + GAMMA*G
states_and_returns.reverse() # we want it to be in order of state visited
return states_and_returns
if __name__ == '__main__':
# use the standard grid again (0 for every step) so that we can compare
# to iterative policy evaluation
grid = standard_grid()
# print rewards
print("rewards:")
print_values(grid.rewards, grid)
# state -> action
# found by policy_iteration_random on standard_grid
# MC method won't get exactly this, but should be close
# values:
# ---------------------------
# 0.43| 0.56| 0.72| 0.00|
# ---------------------------
# 0.33| 0.00| 0.21| 0.00|
# ---------------------------
# 0.25| 0.18| 0.11| -0.17|
# policy:
# ---------------------------
# R | R | R | |
# ---------------------------
# U | | U | |
# ---------------------------
# U | L | U | L |
policy = {
(2, 0): 'U',
(1, 0): 'U',
(0, 0): 'R',
(0, 1): 'R',
(0, 2): 'R',
(1, 2): 'U',
(2, 1): 'L',
(2, 2): 'U',
(2, 3): 'L',
}
# initialize V(s) and returns
V = {}
returns = {} # dictionary of state -> list of returns we've received
states = grid.all_states()
for s in states:
if s in grid.actions:
returns[s] = []
# 빈값을 넣어는다 initializize
else:
# terminal state or state we can't otherwise get to
V[s] = 0
# repeat until convergence
# 5000 iterative
for t in range(5000):
# generate an episode using pi
states_and_returns = play_game(grid, policy)
seen_states = set()
for s, G in states_and_returns:
# check if we have already seen s
# called "first-visit" MC policy evaluation
if s not in seen_states:
returns[s].append(G)
V[s] = np.mean(returns[s])
seen_states.add(s)
print("values:")
print_values(V, grid)
print("policy:")
print_policy(policy, grid)
2. MC for Control Problem
- Let’s now move on to control problem
- Can we use MC?
- Problem: we only have V(s) for a given policy, we don’t know what actions will lead to better V(s) because we can’t do look-ahead search
- only play episode and get states/returns
- key is to use Q(s,a)
- we can choose argmax[a]{Q,a}
MC for Q(s,a)
- simple modification
- instead of list of tuples(s,G)
- return list of triples(s,a,G)
Problem with Q(s,a)
- with V(s) we only need ISI different estimates
- with Q(s,a) we need IsI x IAI different estimates
- Many more iterations of MC are needed
- should remind us of explore-exploit dilemma
- if we follow a fixed policy, we only do 1 action per state
- we can only fill in ISI / (ISI x IAI) = 1 / IAI values in Q
- Can fix it by using the “exploring-starts” methods
- we choose a random initial state and a random initial action
- thereafter follow policy
- this is consistent with our definition of Q :
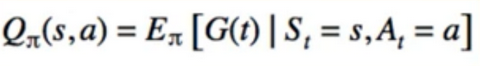
Back to Control Problem
- if we think actually, we’ll realize we already know the answer
- Generalized policy iteration:
- Alternate between policy evaluation and policy improvement
- we know how to do evaluation
- policy improvement same as always : π(s) = $argmax_s$Q(s,a)
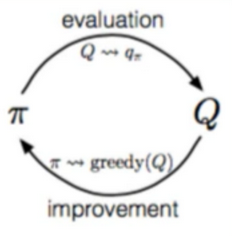
Problem with MC
- Problem: same as before - we have an iterative algorithm inside an iterative algorithm
- For Q we need lots of samples
3. Solution
- Similar value iteration
- Do not start a fresh MC evaluation on each round
- would take too long to collect samples
- instead, just keep updating the same Q
- Do policy improvement after every episode
- therefore, generate only one episode per iteration
Pseudocode
```
Q = random, pi =random
While True :
s, a = randomly select from S and A
states_actions_returns = play_game(start=(s,a))
for s,a,G in state_actions_returns:
returns(s,a).append(G)
Q(s,a) = average(returns(s,a))
for s in states:
pi(s) = argmax[a]{Q(s,a)}
```
Another Problem with MC
- What if policy includes an action that bumps into a wall?
- we end up in same state as before
- if we follow this policy, episode will never finish
- Hack:
- if we end up in same state after doing action, give this a reward of -100, and end the episode
MC-ES
- Interesting fact: this converges even though the samples for Q are for different policies
- if Q is suboptimal, then policy will change, causing Q to change
- we can only achieve stability when both value and policy converge to optimal value and optimal policy
- Another interesting fact: this has never been formally proven
4. MC Control without ES
- Disadvantage of previous control method : needs exploring starts
- Could be infeasible(不可能的) for games we are not playing in “god-mode”
- E.g Self-driving car
- remove need for ES(exploring starts)
- Recall: all the techniques we learned for the multi-armed bandit are applicable here
- let’s not be greedy, but epsilon-greedy instead
- code modification:
- Remove exploring starts
- change policy to sometimes be random
- Epsilon-soft
- But we also use epsilon to decide if we want to explore:
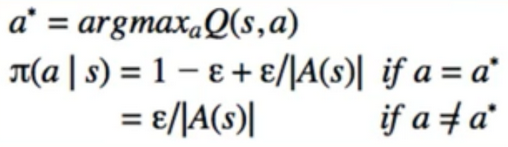
- From now on, we’ll just refer to this as epsilon-greedy
추가 설명
- 즉 해보지 않은 행동에 대해서도 가끔 선택할 수 있게 하는 방법
- 방법에는 두가지가 있다
- On-policy : 결정했던 행동들을 가지고 정책을 평가 발전한다
- Off-Policy : 다른 방법에 의해 만들어진 데이터로 정책 평가와 발전한다.
- Monte Carlo ES는 On-Policy
- Monte Carlo without ES 는 Off-Policy
- On-policy Control 방법은 정책이 Soft 하다. Soft의 뜻은 정책의 모든 확률이 0 이상, 즉 초기에 모든 행동을 일정 확률로 할 가능성이 있다가 점점 결정적인 최적의 정책으로 바뀐다(deterministic Optimal Policy).
- Off-Policy Control은 Epsilon Greedy 방법을 이용하여 랜덤하게 행동을 선택할 확률 최소값은 Epsilon / IA(s)I 이며, 나머지 확률 1-epsilon+epsilon/IA(s)I 로 greedy 행동을 취한다. (1-epsilon에 epsilon/IA(s)I 추가한 이유는 랜덤하게 하는 행동중 하나가 이 greedy로 행동 할 것이기 때문이다.)
- epsilon-greedy 정책은 확률이 π(a I s) >= epsilon/IA(s)I로, e-soft policy의 예이다.
- 즉 exporing starts 가정 없이 탐험을 할 수 없기 때문에 무작정 가치를 따라 Greedy하게 행동하도록 할 수 없다.
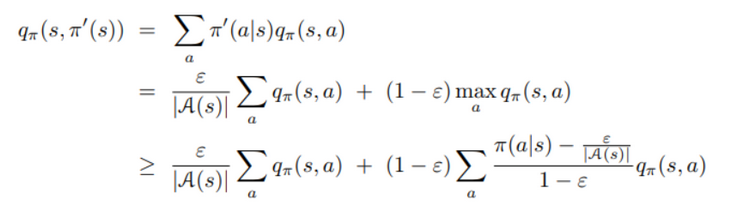
- epsilon-greedy policy 또한 정책 개선 이론에 따라 확실히 개선된다. π’를 epsilon-greedy policy라고 하였을 때( weighted average가 1 이고, 가장 큰 수보다 작거나 같다. 아래식은 모든 행동에 대한 확률의 합이 1이 되도록 한 식이다.)
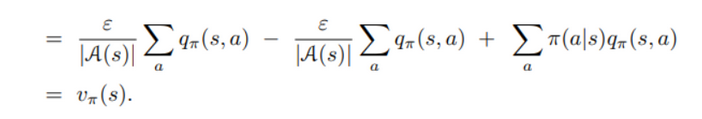
- 결국 정책 x의 가치의 합이기 때문에 이는 상태 가치홤수와 같다. 결국 $q_π$(s,π’(s))>=$v_π$(s) 이므로, 정책 개선 이론에 따라 π’>=π(즉 $v+π$(s)>=$v_π$(s))가 된다.
-
epsilon-soft policy 과에 차이점은 epsilon-soft가 들어갔다는 차이밖에 없다. 동일한 행동과 상태들, epsilon에 따라 랜덤한 행동을 하는 것까지 같다. 아래에 variable $v_$^~ $q_$^~ 이 새로운 환경에 최적의 가치 함수들이라고 하자. 그럼 epsilon-soft policy 는 $v_π$ = $v_π$^~라면 π는 최적이라고 할 수 있을 것이다.
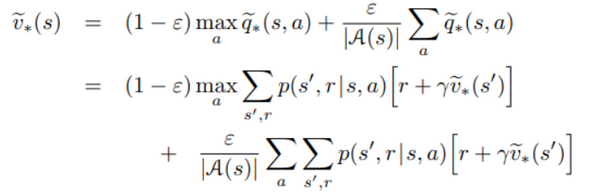
- $v_π$ = $v_π$^~ 로 바꾸면
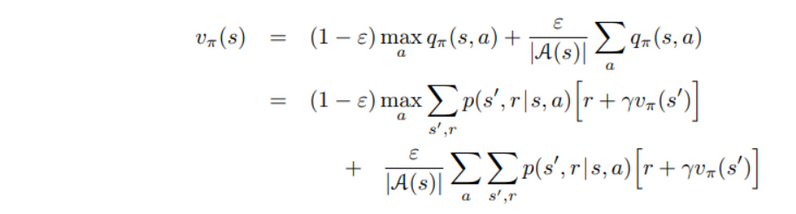
- Policy iteration은 epsilon-soft policy 에도 적용이 된다는 것을 보였을 것이다. epsilon-soft-poilicy 에 greedy policy를 적용하면 매 step마다 개선이 확실 된다는 것을 보이며, exploring starts를 제거했다.
How often will we reach off-policy states?
- Consider a state K steps away from the start
- the probability that we get there by pure exploration is small
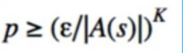
- we need to run MC many times to converge for these states
5. MC Summary
- Last Section, DP: we knew all the state transition probability and never played the game
- this section: learn from experience
- main idea: approximate the expected return with sample mean
- First-visit and every-visit
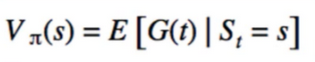
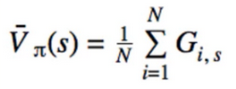
MC VS DP
- MC can be more efficient than DP because we don’t need to loop through all states
- But also means we might not get the “full” value function, since some states will never be reached or reached very rarely
- more data -> more accuracy
- We used exploring starts to ensure we had adequate data for each state
MC Control
- Use Q instead of V
- No look-ahead search
- Problem: MC loop inside another loop
- We took the same approach as value iteration: update the policy after every episode, keep updating the same Q in-place
- Surprising: it converges even though the samples are not all for the same policy
- Never formally proved to converge
- we then removed exploring starts assumption by replacing it with epsilon-greedy
- MDPs are like different multi-armed bandit problem at each state
Reference:
Artificial Intelligence Reinforcement Learning
Montel Carlo(MC) Methods Introduction
- Last Section: Dynamic Programming
- would that work for self-driving cars or video games?
- can i just set the state of the agent?
- “god-mode” capabilities?
- MC Methods learn purely from experience
- Montel Carlo usually refers to any method with a significant random component
- Random Component in RL is the return
- With MC, instead of calculating the true expected value of G, we calculate its sample mean
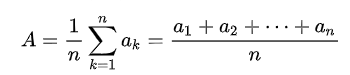
- Need to assume episode tasks only
- Episode must terminate before we calculate return
- Not “fully” online since we need to wait for entire episode to finish before updating
- (full online mean is update after every action)
- monte carlo methods is not fully online which mean it is updated after episode to finish
- Should Remind you of multi-armed bandit
- Multi-Armed bandit : average reward after every action
- MDPs: average the return
- One way to think of MC-MDP is every state is a separate multi-armed bandit problem
- Follow the same pattern
- Prediction Problem(Finding Value given policy)
- Control Problem(finding optimal policy)
1. Monte Carlo for prediction Problem
How do we generate G?
- just play a bunch of episode, log the states and reward sequences
s1 s2 s3 ... sT r1 r2 r3 ... rT -
Calculate G from Definition: G(t) = r(t+1)+gamma*G(t+1)
- very helpful to calculate G by iterating through states in reverse order
- Once we have(s,G) pairs, average them for each s
Multiple Visits to s
- what if we see the same state more than once in an episode
- E.g. we see s at t=1 and t=3
- which return should we use? G(1) or G(3
- First-visit method :
- Use t = 1 only
- Every-visit method :
- Use both t=1 and t=3 as samples
- Surprisingly, it has been proven that both lead to same answer
First-Visit MC Pseudocode
def first_visit_monte_carlo_prediction(π, N):
V = random initialization
all_return = {} # default = []
do N times:
states, returns = play_episode
for s, g in zip(states, returns):
if not seen s in this episode yet:
all_return[s].append(g)
V(s) = sample_mean(all_returns[s])
return V
Sample Mean
- Notice how we store all returns in a list
- Didn’t we discuss how that’s inefficient?
- Can also use previous mean to calculate current mean
- Can also use moving average for non-stationary problems
- Everything we learned before still applies
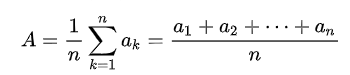
- Rules of probability still apply
- Central limit Theorem
- Variance of estimate = Variance of RV(Random Value) / N
Calculating Returns from Rewards
s = grid.current_state()
states_and_rewards = [(s,0)]
while not game_over:
a = policy(s)
r = grid.move(a)
s = grid.current_state()
states_and_rewards.append((s,r))
G = 0
states_and_returns = []
for s,r in reverse(states_and_rewards):
states_and_returns.((s,G))
G = r + gamma*G
states_and_returns.reverse
MC
- Recall: one Disadvantage of DP is that we need to loop through all states
- MC: only update V for visited states
- We don’t even need to know what all the states are, we can just discover them as we play
2. MC for Windy Gridworld
- Windy Gridworld, different policy
- Policy/transitions were deterministic, MC not really needed
- in windy gridworld, p(s’r I s,a) not deterministic
- with this policy, we try to get to goal
- Values can be -ve, if overall wind pushes us to losing state more often
code
# https://deeplearningcourses.com/c/artificial-intelligence-reinforcement-learning-in-python
# https://www.udemy.com/artificial-intelligence-reinforcement-learning-in-python
from __future__ import print_function, division
from builtins import range
# Note: you may need to update your version of future
# sudo pip install -U future
import numpy as np
from grid_world import standard_grid, negative_grid
from iterative_policy_evaluation import print_values, print_policy
SMALL_ENOUGH = 1e-3
GAMMA = 0.9
ALL_POSSIBLE_ACTIONS = ('U', 'D', 'L', 'R')
# NOTE: this is only policy evaluation, not optimization
def random_action(a):
# choose given a with probability 0.5
# choose some other a' != a with probability 0.5/3
p = np.random.random()
if p < 0.5:
return a
else:
tmp = list(ALL_POSSIBLE_ACTIONS)
tmp.remove(a)
return np.random.choice(tmp)
def play_game(grid, policy):
# returns a list of states and corresponding returns
# reset game to start at a random position
# we need to do this, because given our current deterministic policy
# we would never end up at certain states, but we still want to measure their value
start_states = list(grid.actions.keys())
start_idx = np.random.choice(len(start_states))
grid.set_state(start_states[start_idx])
# random start
s = grid.current_state()
states_and_rewards = [(s, 0)] # list of tuples of (state, reward)
while not grid.game_over():
a = policy[s]
a = random_action(a)
r = grid.move(a)
s = grid.current_state()
states_and_rewards.append((s, r))
# calculate the returns by working backwards from the terminal state
G = 0
states_and_returns = []
first = True
for s, r in reversed(states_and_rewards):
# the value of the terminal state is 0 by definition
# we should ignore the first state we encounter
# and ignore the last G, which is meaningless since it doesn't correspond to any move
if first:
first = False
else:
states_and_returns.append((s, G))
G = r + GAMMA*G
states_and_returns.reverse() # we want it to be in order of state visited
return states_and_returns
if __name__ == '__main__':
# use the standard grid again (0 for every step) so that we can compare
# to iterative policy evaluation
grid = standard_grid()
# print rewards
print("rewards:")
print_values(grid.rewards, grid)
# state -> action
# found by policy_iteration_random on standard_grid
# MC method won't get exactly this, but should be close
# values:
# ---------------------------
# 0.43| 0.56| 0.72| 0.00|
# ---------------------------
# 0.33| 0.00| 0.21| 0.00|
# ---------------------------
# 0.25| 0.18| 0.11| -0.17|
# policy:
# ---------------------------
# R | R | R | |
# ---------------------------
# U | | U | |
# ---------------------------
# U | L | U | L |
policy = {
(2, 0): 'U',
(1, 0): 'U',
(0, 0): 'R',
(0, 1): 'R',
(0, 2): 'R',
(1, 2): 'U',
(2, 1): 'L',
(2, 2): 'U',
(2, 3): 'L',
}
# initialize V(s) and returns
V = {}
returns = {} # dictionary of state -> list of returns we've received
states = grid.all_states()
for s in states:
if s in grid.actions:
returns[s] = []
# 빈값을 넣어는다 initializize
else:
# terminal state or state we can't otherwise get to
V[s] = 0
# repeat until convergence
# 5000 iterative
for t in range(5000):
# generate an episode using pi
states_and_returns = play_game(grid, policy)
seen_states = set()
for s, G in states_and_returns:
# check if we have already seen s
# called "first-visit" MC policy evaluation
if s not in seen_states:
returns[s].append(G)
V[s] = np.mean(returns[s])
seen_states.add(s)
print("values:")
print_values(V, grid)
print("policy:")
print_policy(policy, grid)
2. MC for Control Problem
- Let’s now move on to control problem
- Can we use MC?
- Problem: we only have V(s) for a given policy, we don’t know what actions will lead to better V(s) because we can’t do look-ahead search
- only play episode and get states/returns
- key is to use Q(s,a)
- we can choose argmax[a]{Q,a}
MC for Q(s,a)
- simple modification
- instead of list of tuples(s,G)
- return list of triples(s,a,G)
Problem with Q(s,a)
- with V(s) we only need ISI different estimates
- with Q(s,a) we need IsI x IAI different estimates
- Many more iterations of MC are needed
- should remind us of explore-exploit dilemma
- if we follow a fixed policy, we only do 1 action per state
- we can only fill in ISI / (ISI x IAI) = 1 / IAI values in Q
- Can fix it by using the “exploring-starts” methods
- we choose a random initial state and a random initial action
- thereafter follow policy
- this is consistent with our definition of Q :
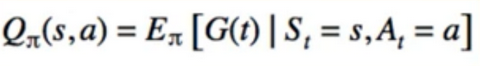
Back to Control Problem
- if we think actually, we’ll realize we already know the answer
- Generalized policy iteration:
- Alternate between policy evaluation and policy improvement
- we know how to do evaluation
- policy improvement same as always : π(s) = $argmax_s$Q(s,a)

Problem with MC
- Problem: same as before - we have an iterative algorithm inside an iterative algorithm
- For Q we need lots of samples
3. Solution
- Similar value iteration
- Do not start a fresh MC evaluation on each round
- would take too long to collect samples
- instead, just keep updating the same Q
- Do policy improvement after every episode
- therefore, generate only one episode per iteration
Pseudocode ``` Q = random, pi =random
While True : s, a = randomly select from S and A states_actions_returns = play_game(start=(s,a)) for s,a,G in state_actions_returns: returns(s,a).append(G) Q(s,a) = average(returns(s,a)) for s in states: pi(s) = argmax[a]{Q(s,a)} ```
Another Problem with MC
- What if policy includes an action that bumps into a wall?
- we end up in same state as before
- if we follow this policy, episode will never finish
- Hack:
- if we end up in same state after doing action, give this a reward of -100, and end the episode
MC-ES
- Interesting fact: this converges even though the samples for Q are for different policies
- if Q is suboptimal, then policy will change, causing Q to change
- we can only achieve stability when both value and policy converge to optimal value and optimal policy
- Another interesting fact: this has never been formally proven
4. MC Control without ES
- Disadvantage of previous control method : needs exploring starts
- Could be infeasible(不可能的) for games we are not playing in “god-mode”
- E.g Self-driving car
- remove need for ES(exploring starts)
- Recall: all the techniques we learned for the multi-armed bandit are applicable here
- let’s not be greedy, but epsilon-greedy instead
- code modification:
- Remove exploring starts
- change policy to sometimes be random
- Epsilon-soft
- But we also use epsilon to decide if we want to explore:
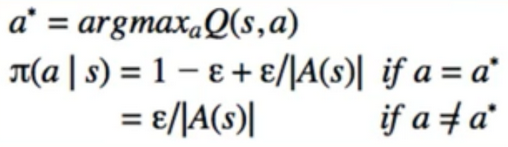
- From now on, we’ll just refer to this as epsilon-greedy
추가 설명
- 즉 해보지 않은 행동에 대해서도 가끔 선택할 수 있게 하는 방법
- 방법에는 두가지가 있다
- On-policy : 결정했던 행동들을 가지고 정책을 평가 발전한다
- Off-Policy : 다른 방법에 의해 만들어진 데이터로 정책 평가와 발전한다.
- Monte Carlo ES는 On-Policy
- Monte Carlo without ES 는 Off-Policy
- On-policy Control 방법은 정책이 Soft 하다. Soft의 뜻은 정책의 모든 확률이 0 이상, 즉 초기에 모든 행동을 일정 확률로 할 가능성이 있다가 점점 결정적인 최적의 정책으로 바뀐다(deterministic Optimal Policy).
- Off-Policy Control은 Epsilon Greedy 방법을 이용하여 랜덤하게 행동을 선택할 확률 최소값은 Epsilon / IA(s)I 이며, 나머지 확률 1-epsilon+epsilon/IA(s)I 로 greedy 행동을 취한다. (1-epsilon에 epsilon/IA(s)I 추가한 이유는 랜덤하게 하는 행동중 하나가 이 greedy로 행동 할 것이기 때문이다.)
- epsilon-greedy 정책은 확률이 π(a I s) >= epsilon/IA(s)I로, e-soft policy의 예이다.
- 즉 exporing starts 가정 없이 탐험을 할 수 없기 때문에 무작정 가치를 따라 Greedy하게 행동하도록 할 수 없다.
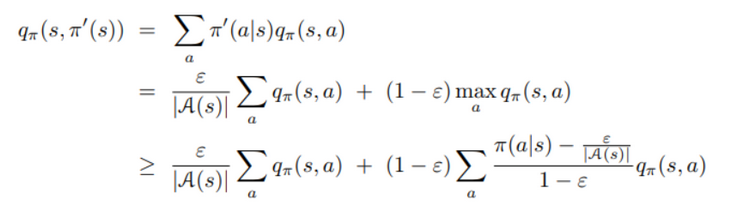
- epsilon-greedy policy 또한 정책 개선 이론에 따라 확실히 개선된다. π’를 epsilon-greedy policy라고 하였을 때( weighted average가 1 이고, 가장 큰 수보다 작거나 같다. 아래식은 모든 행동에 대한 확률의 합이 1이 되도록 한 식이다.)
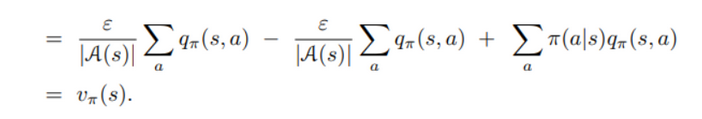
- 결국 정책 x의 가치의 합이기 때문에 이는 상태 가치홤수와 같다. 결국 $q_π$(s,π’(s))>=$v_π$(s) 이므로, 정책 개선 이론에 따라 π’>=π(즉 $v+π$(s)>=$v_π$(s))가 된다.
-
epsilon-soft policy 과에 차이점은 epsilon-soft가 들어갔다는 차이밖에 없다. 동일한 행동과 상태들, epsilon에 따라 랜덤한 행동을 하는 것까지 같다. 아래에 variable $v_$^~ $q_$^~ 이 새로운 환경에 최적의 가치 함수들이라고 하자. 그럼 epsilon-soft policy 는 $v_π$ = $v_π$^~라면 π는 최적이라고 할 수 있을 것이다.
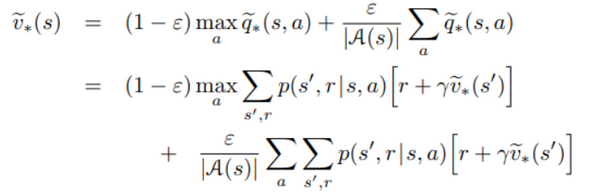
- $v_π$ = $v_π$^~ 로 바꾸면
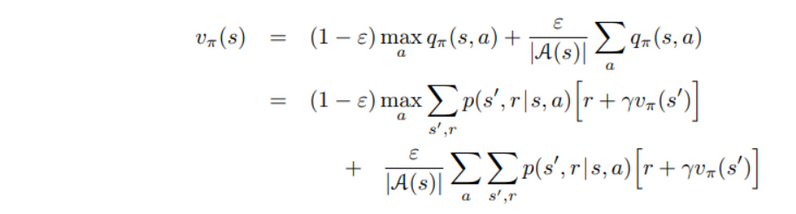
- Policy iteration은 epsilon-soft policy 에도 적용이 된다는 것을 보였을 것이다. epsilon-soft-poilicy 에 greedy policy를 적용하면 매 step마다 개선이 확실 된다는 것을 보이며, exploring starts를 제거했다.
How often will we reach off-policy states?
- Consider a state K steps away from the start
- the probability that we get there by pure exploration is small
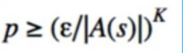
- we need to run MC many times to converge for these states
5. MC Summary
- Last Section, DP: we knew all the state transition probability and never played the game
- this section: learn from experience
- main idea: approximate the expected return with sample mean
- First-visit and every-visit
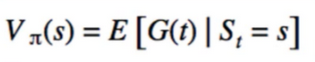
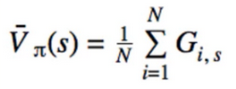
MC VS DP
- MC can be more efficient than DP because we don’t need to loop through all states
- But also means we might not get the “full” value function, since some states will never be reached or reached very rarely
- more data -> more accuracy
- We used exploring starts to ensure we had adequate data for each state
MC Control
- Use Q instead of V
- No look-ahead search
- Problem: MC loop inside another loop
- We took the same approach as value iteration: update the policy after every episode, keep updating the same Q in-place
- Surprising: it converges even though the samples are not all for the same policy
- Never formally proved to converge
- we then removed exploring starts assumption by replacing it with epsilon-greedy
- MDPs are like different multi-armed bandit problem at each state
Reference:
Artificial Intelligence Reinforcement Learning

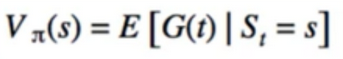
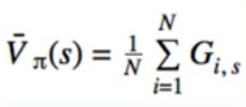
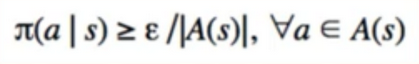
Comments