14. Approximation Methods
30 Sep 2019 | Reinforcement Learning
Approximation Methods
- Major Disadvantage of methods we’ve learned
- V - Need to estimate ISI values
- Q - Need to estimate ISI x IAI values
- ISI and IAI can be very large
- solution : Approximation
- Recall: neural networks are universal function approximator
- First, we do feature extraction: convert state s to feature vector x
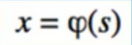
- we want a function, parameterized by theta, that accurately approximates V
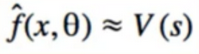
1. Linear Approximation
- Function approximation methods requires us to use models that are differentiable
- Can’t use something like decision tree or k-nearest neighbour
- in sequal(查询语言) to this section, we will use deep learning methods, which are differentiable
- Neural networks don’t require us to engineer features beforehand, but it can help
- FOr Approximation methods, we will need linear regression and gradient descent
2. Section outline
- MC prediction
- TD(0) prediction
- SARSA
3. Sanity(明智) Checking
- we can always sanity check our work by comparing to non-approximated versions
- we expect approximation to be close, but perhaps not exactly equal
- Obstacle we may encounter: our code is implemented perfectly, but our model is bad
- Linear models are not very expressive
- if we extract a poor set of features, model won’t learn value function well
- will need to put in manual work to do feature engineering
4. Linear Model
- Supervised learning aka,Function Approximation
- The function we are trying to approximate is V(s) or Q(s,a)
- Rewards are real numbers
- So returns, which are sums of rewards are real number
- 2 Supervised learning techniques
- Classification
- regression
- we are doing regression
5. Error
- Supervised Learning methods have cost Functions
- Regression means squared error is the appropriate choice
- Squared difference between V and estimate of V
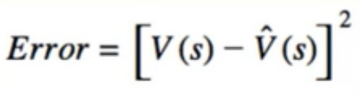
- Replace V with its definition
- But we don’t know this expected value
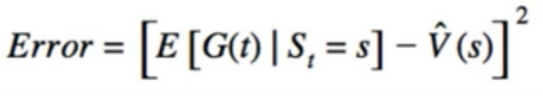
- as we learned from MC(Monte Carlo), we can replace the expected value with its sample means
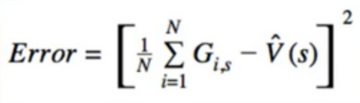
- Alternatively, we can treat each G_(i,s) as a training sample
- And try to minimize all the individual squared differences simultaneously(just like linear regression)
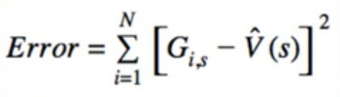
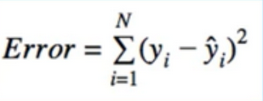
6. stochastic Gradient Descent
- we can now do stochastic(随机的) gradient decent
- Move in direction of gradient of error wrt only one sample at a time
Gradient Descent 설명
- Neural Network의 loss function의 현 weight의 기울기(gradient)를 구하고 Loss를 줄이는 방향으로 업데이트 나가는 방법
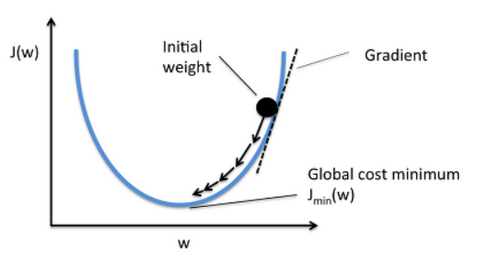
- Loss function (ERROR) 는 현재 가중치(weight)에서 틀린 정도를 알려주는 함수이다.
- 즉, 현재 네트워크의 weight에서 내가 가진 데이터를 집어 넣으면 에러가 생길 것이다. 거기에 미분을 하면 에러를 줄이는 방향을 알 수 있다.
- 그 방향으로 정해진 Learning rate를 통해서 weight를 이동시킨다. 이것을 반복해서 학습하는 것이다.
- 즉 Gradient Descent는 현재 네트워크의 Weight에 어떤 데이터를 넣을 떄 에러값을 미분해서 에러의 방향(Gradient)을 알애체고 그 방향으로 정해진 Learning rate를 통해서 weight을 이동시킨다(Descent).

- Gradient Descent의 단점은 가진 데이터를 다 넣으면 전체 에러가 계산이 될 것이다.
- 그렇기 때문에 최적값을 찾아 나가기 위해서 한칸 전진할 때마다 모든 데이터 셋을 넣어주어야 해야하기 때문에 학습이 굉장히 오래 걸리는 문제가 발생하게 된다.
- 그럼 Gradient Descent 말고 더 빠른 Optimizer 는 없을까? 그것이 바로 stochastic Gradient Descent 이다.
Stochastic Gradient Descent
- Stochastic Gradient Descent(SGD)는 조금만 흝어보고(Mini Batch)빠르게 학습 하는 것이다.
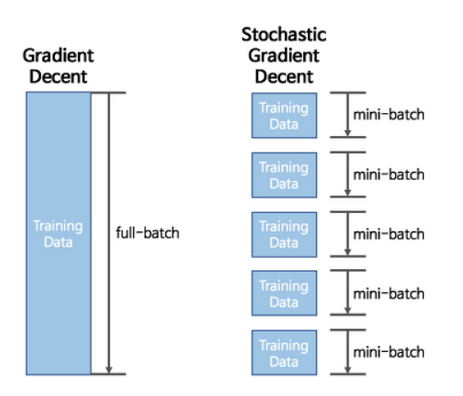
- 최적값을 찾아 과정은 이와 같다
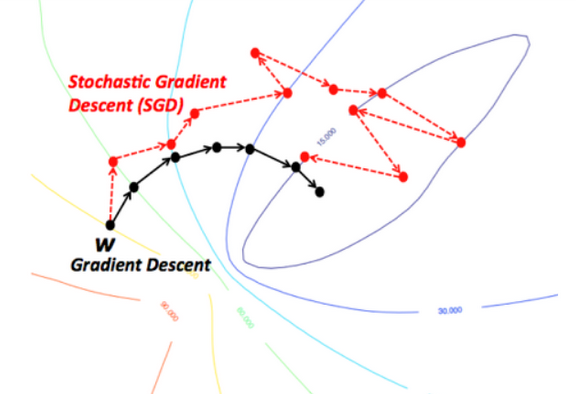
- GD의 경우 항상 전체 데이터 셋을 가지고 Learning rate로 최적의 값을 찾아가는 모습을 불 수 있다.
- SGD 같은 경우 Mini-batch 사이즈 만큼 조금씩 돌려서 최적의 값으로 찾아나간다.
7. Gradient Descent
Gradient Descent for Linear Models
8. Relationship to Montel Carlo
- Recall when we did not parameterized V(s) - as if V(s) itself was a parameter
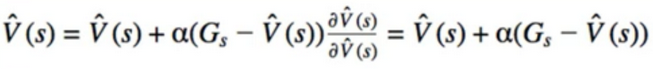
- this is the exact same equation we had before for Mote Carlo
- therefore, what we were doing was an instance of gradient descent
9. Feature Engineering
- Recall: neural networks can in some sense find good nonlinear transformations / features of the raw data
- since we only study linear methods in the past section, we need to find features manually
- Feature Engineering 머신러닝 알고리즘을 작동하기 위해 데이터에 대한 도메인 지식을 활용하여 특징(Feature)을 만들어 내는 것
- 머신러닝 모델을 위한 데이터 테이블의 column(특징)을 생성하거나 선택하는 작업을 의미
- 즉 모델의 성능을 높이기 위해 초기 주어진 데이터로부터 특징을 가공하고 생성하는 전체 과정
- Feature Engineering 모델 성능에 미치는 영향이 크기 때문에 머신러닝 응용에 있어서 굉장히 중요한 단계
- Feature Engineering 아래와 같은 단계에 구성되어 있다.
- Project scoping(Define Problem)
- Data Collection
- EDA
- Data Preprocessing
- Feature Engineering
- Modeling
- Evaluation
- Project Delivery / Insights
- Feature Eingeering은 모델에 입력하기 전 단계에 데이터의 특성을 잘 반영하고 성능을 높일 수 있도록 특징을 생성하고 가공하는 단계이다.
- Feature Engineering에 구성은 아래와 같다.
방법적인 측면
- Feature Selection(특징 선택)
- 특징 랭킹(Feature Ranking) 또는 특징 중요도 (Feature Importance)라고도 불린다.
- 불류 모델 중 Decision Tree 같은 경우 트리의 상단에 있을 수록 중요도가 높으므로 이를 반영하여 특징 별로 중요도를 매긴다.
- 회귀 모델의 경우 Forward Selection 과 Backward Elimination 같은 알고리즘을 통해 특징을 선택한다.
- Dimension Reduction(차원 감소)
- Dimension Reduction은 Feature extraction(특징 추출)이라는 말로도 불린다.
- 차원 축소는 데이터의 압축이나 잡음을 제거하는 효과도 있지만, 관측 데이터를 잘 설명할 수 있는 잠재 공간(Latent space)을 찾는 것이다.
- 가장 대표적인 알고리즘은 PCA(Principle Component Analysis)
- PCA는 각 Feature(변수)를 하나의 축으로 투영시켰을 때 분산이 가장 큰 축을 첫번째 주성분으로 선택하고 그다음 큰 축을 두번째 주성분으로 선택하고 데이터를 선형 변환하여 다차원을 축소하는 방법이다.
Domain(분야) 전문성 측면
- Feature Generation(특징 생성) or Feature Construction(특징 구축)
- 이 방법을 주로 Feature Engineering 이라고 말한다.
- 초기에 주어진 데이터로 부터 모델링 성능을 높이는 새로운 특징을 만드는 과정이다.
- 이때 데이터에 대한 Domain(분야) 전문성을 바탕으로 데이터를 합치거나 쪼개는 등을 거쳐 Feature을 만들게 된다.
- 간단한 예로 시간 데이터를 AM/PM으로 나누는 것이다.
- 이 작업은 한번 해서 끝나는 것이 아니라 끊임 없이 모델링 성능을 높이는 목적으로 반복해서 작업할 수 있는 부분이기 때문에 전문성과 경험에 따라 비용과 시간을 줄일 수 있는 부분이다.
Mapping s -> x
- states can be thought of as categorical variable
- (0,0) -> category 1
- (0,1) -> category 2
- etc
- how do we treat categorical variable? One-Hot encoding
- what if we do one-hot encoding?
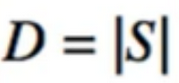
- s=(0,0) -> x=[1,0,0,..]
- s=(0,1) -> x=[0,1,0,..]
- D is the cardinality(基数) of S
- 집합의 cardinality는 집합의 원소의 개수를 말한다.
- 두 집합 A,B가 cardinal number가 같다고 함은 일대일 대응 f: A–> B가 존재하는 것이다.
- 따라서 두 집합 A,B cardinal number가 같다면 원소의 개수가 같은것이다.
- Problem with one-hot encoding: this requires the same number of parameters as measuring V(s) directly
- i.e. V is a dict with ISI keys and ISI values
- if we do one-hot encoding, each Component $θ_i$ actually represents V(s=i) itself
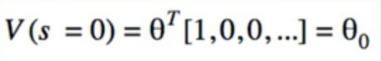
One-Hot Encoding
- one positive aspect to using one-hot encoding
- suppose our code is not working(our V isn’t accurate)
- we can have perfectly good code/no bugs, but still might not yield good results because feature are bad
- Change feature transformer to use one-hot encoding
- if it starts working, that confirm our features are bat(since it’s the same as a non-approximate method)
Alternative to One-Hot
- in case of GridWorld, each(i,j) represents a position in 2-D space
- it’s more like 2 real numbers than a category
- Vector x can be (i,j) itself
- could scale it so mean = 0 and var = 1
- this x is the “raw data”
- problem
Polynomials
- Recall from linear regression class: we can make new features by creating polynomials
- Recall from calculus: infinite taylor expansion can approximate any function
- Ex. second order terms
- $x_1$^2
- $x_2$^2
- $x_1$$x_2$
- don’t overfit
10. Approximation MC Prediction
- Replace V(s) with linear model
- there are two main steps
- With Approximation
Pseudocode
def mc_approx_prediction(π):
θ = random
for i = 1..N
states_and_returns = play_game
for s, g in states_and_returns:
x = Φ(s)
θ = θ + α(g-θ^T*x)x
11. Approximation TD(0)
- apply approximation to TD(0) -> but one caveat(警告)
- Main difference between MC and TD(0): instead of Using G, we use r+ɣV(s’)

- Problem
- the target is not a real target, because it require a model prediction
- Gradient is not a true gradient, so we call it a “Semi-Gradient”
- Remember don’t need to calculate returns, use rewards directly
12. Semi-Gradient SARSA
- SARSA with approximation
- we will approximate Q
- More difficult than Approximating V, Since instead of approximating ISI value, we need to approximate ISI x IAI values
- Model Prediction appears in target again, so this is another instance of semi gradient
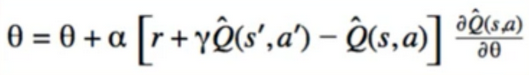
- Features
- Need to combine(s,a) -> x
- Simple Idea: take our old encoding of s(r,c,r*c) and add one-hot encoding of action
- x = (r,c,r*c,U,D,L,R,1)
- r,c is the raw and column
- it well not approximate Q well but try to find it
- Best Features
x = [
r && U,
c* && U,
r*r && U,
c*c && U,
r*c && U,
l && U,
r && D,
]
- 6 per action x 4actions + 1bias = 25 features
- tabular method : 9states x 4actions = 36
- action value function을 Q-Table로 작성하여 푸는 방법을 Tabular Methods
- Tabular Methods를 state 나 action이 작을때만 적용 가능 하다고 한다.
- 왜냐하면 각각의 state에 action마다 Q값을 넣어줘야 하기 때문이다. 그래서 실제 환경이나 실생활, 혹은 연속적인 환경에서는 적용을 할 수 없다.
- Similar to NLP: word2idx is a dict that maps each word to a unique index in x
- SA2IDX(Semi-gradient SARSA) is a dict that maps(s,a) to a unique index in x
13. Summary
- State Space can grow too large to feasibly enumerate
- Approximation methods allow us to compress number of parameters needed
- differentiable Models are a good fit, because we can use stochastic gradient decent
- Online Learning is good because if we have a long episode, agent can learn during the episode
- Everything we learned is just as applicable to deep learning / neural nets
- x = (i,j) is not expressive enough, so we used feature engineering
- we applied approximation to:
- MC Prediction
- TD(0) Prediction(semi-Gradient)
- SARSA(Semi-Gradient)
- Why didn’t we apply approximation to Q-Learning?
- Q-learning is an off-policy method
- Sources have stated approximation for off-policy control methods do not have good convergence characteristics (utton & Barto)
- we are encouraged to modify SARSA to use Q-learning instead
- Recall: with Q-learning the a’ we use in update is not necessarily the action we will take next
- but it has been done at “Deep Q Learning”
- we’re encouraged to modify SARSA to use Q-Learning instead
Reference:
Artificial Intelligence Reinforcement Learning
Approximation Methods
- Major Disadvantage of methods we’ve learned
- V - Need to estimate ISI values
- Q - Need to estimate ISI x IAI values
- ISI and IAI can be very large
- solution : Approximation
- Recall: neural networks are universal function approximator
- First, we do feature extraction: convert state s to feature vector x
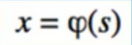
- we want a function, parameterized by theta, that accurately approximates V
1. Linear Approximation
- Function approximation methods requires us to use models that are differentiable
- Can’t use something like decision tree or k-nearest neighbour
- in sequal(查询语言) to this section, we will use deep learning methods, which are differentiable
- Neural networks don’t require us to engineer features beforehand, but it can help
- FOr Approximation methods, we will need linear regression and gradient descent
2. Section outline
- MC prediction
- TD(0) prediction
- SARSA
3. Sanity(明智) Checking
- we can always sanity check our work by comparing to non-approximated versions
- we expect approximation to be close, but perhaps not exactly equal
- Obstacle we may encounter: our code is implemented perfectly, but our model is bad
- Linear models are not very expressive
- if we extract a poor set of features, model won’t learn value function well
- will need to put in manual work to do feature engineering
4. Linear Model
- Supervised learning aka,Function Approximation
- The function we are trying to approximate is V(s) or Q(s,a)
- Rewards are real numbers
- So returns, which are sums of rewards are real number
- 2 Supervised learning techniques
- Classification
- regression
- we are doing regression
5. Error
- Supervised Learning methods have cost Functions
- Regression means squared error is the appropriate choice
- Squared difference between V and estimate of V
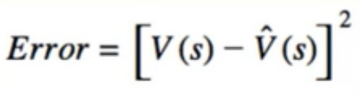
- Replace V with its definition
- But we don’t know this expected value
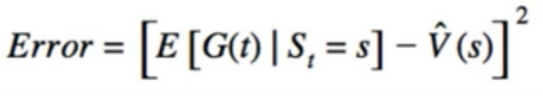
- as we learned from MC(Monte Carlo), we can replace the expected value with its sample means
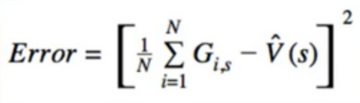
- Alternatively, we can treat each G_(i,s) as a training sample
- And try to minimize all the individual squared differences simultaneously(just like linear regression)
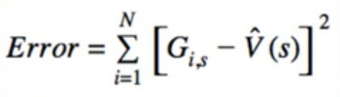
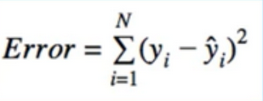
6. stochastic Gradient Descent
- we can now do stochastic(随机的) gradient decent
- Move in direction of gradient of error wrt only one sample at a time
Gradient Descent 설명
- Neural Network의 loss function의 현 weight의 기울기(gradient)를 구하고 Loss를 줄이는 방향으로 업데이트 나가는 방법

- Loss function (ERROR) 는 현재 가중치(weight)에서 틀린 정도를 알려주는 함수이다.
- 즉, 현재 네트워크의 weight에서 내가 가진 데이터를 집어 넣으면 에러가 생길 것이다. 거기에 미분을 하면 에러를 줄이는 방향을 알 수 있다.
- 그 방향으로 정해진 Learning rate를 통해서 weight를 이동시킨다. 이것을 반복해서 학습하는 것이다.
- 즉 Gradient Descent는 현재 네트워크의 Weight에 어떤 데이터를 넣을 떄 에러값을 미분해서 에러의 방향(Gradient)을 알애체고 그 방향으로 정해진 Learning rate를 통해서 weight을 이동시킨다(Descent).

- Gradient Descent의 단점은 가진 데이터를 다 넣으면 전체 에러가 계산이 될 것이다.
- 그렇기 때문에 최적값을 찾아 나가기 위해서 한칸 전진할 때마다 모든 데이터 셋을 넣어주어야 해야하기 때문에 학습이 굉장히 오래 걸리는 문제가 발생하게 된다.
- 그럼 Gradient Descent 말고 더 빠른 Optimizer 는 없을까? 그것이 바로 stochastic Gradient Descent 이다.
Stochastic Gradient Descent
- Stochastic Gradient Descent(SGD)는 조금만 흝어보고(Mini Batch)빠르게 학습 하는 것이다.

- 최적값을 찾아 과정은 이와 같다

- GD의 경우 항상 전체 데이터 셋을 가지고 Learning rate로 최적의 값을 찾아가는 모습을 불 수 있다.
- SGD 같은 경우 Mini-batch 사이즈 만큼 조금씩 돌려서 최적의 값으로 찾아나간다.
7. Gradient Descent
Gradient Descent for Linear Models
8. Relationship to Montel Carlo
- Recall when we did not parameterized V(s) - as if V(s) itself was a parameter
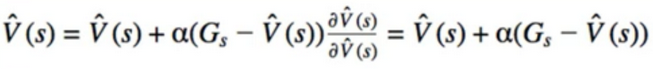
- this is the exact same equation we had before for Mote Carlo
- therefore, what we were doing was an instance of gradient descent
9. Feature Engineering
- Recall: neural networks can in some sense find good nonlinear transformations / features of the raw data
- since we only study linear methods in the past section, we need to find features manually
- Feature Engineering 머신러닝 알고리즘을 작동하기 위해 데이터에 대한 도메인 지식을 활용하여 특징(Feature)을 만들어 내는 것
- 머신러닝 모델을 위한 데이터 테이블의 column(특징)을 생성하거나 선택하는 작업을 의미
- 즉 모델의 성능을 높이기 위해 초기 주어진 데이터로부터 특징을 가공하고 생성하는 전체 과정
- Feature Engineering 모델 성능에 미치는 영향이 크기 때문에 머신러닝 응용에 있어서 굉장히 중요한 단계
- Feature Engineering 아래와 같은 단계에 구성되어 있다.
- Project scoping(Define Problem)
- Data Collection
- EDA
- Data Preprocessing
- Feature Engineering
- Modeling
- Evaluation
- Project Delivery / Insights
- Feature Eingeering은 모델에 입력하기 전 단계에 데이터의 특성을 잘 반영하고 성능을 높일 수 있도록 특징을 생성하고 가공하는 단계이다.
- Feature Engineering에 구성은 아래와 같다.
방법적인 측면
- Feature Selection(특징 선택)
- 특징 랭킹(Feature Ranking) 또는 특징 중요도 (Feature Importance)라고도 불린다.
- 불류 모델 중 Decision Tree 같은 경우 트리의 상단에 있을 수록 중요도가 높으므로 이를 반영하여 특징 별로 중요도를 매긴다.
- 회귀 모델의 경우 Forward Selection 과 Backward Elimination 같은 알고리즘을 통해 특징을 선택한다.
- Dimension Reduction(차원 감소)
- Dimension Reduction은 Feature extraction(특징 추출)이라는 말로도 불린다.
- 차원 축소는 데이터의 압축이나 잡음을 제거하는 효과도 있지만, 관측 데이터를 잘 설명할 수 있는 잠재 공간(Latent space)을 찾는 것이다.
- 가장 대표적인 알고리즘은 PCA(Principle Component Analysis)
- PCA는 각 Feature(변수)를 하나의 축으로 투영시켰을 때 분산이 가장 큰 축을 첫번째 주성분으로 선택하고 그다음 큰 축을 두번째 주성분으로 선택하고 데이터를 선형 변환하여 다차원을 축소하는 방법이다.
Domain(분야) 전문성 측면
- Feature Generation(특징 생성) or Feature Construction(특징 구축)
- 이 방법을 주로 Feature Engineering 이라고 말한다.
- 초기에 주어진 데이터로 부터 모델링 성능을 높이는 새로운 특징을 만드는 과정이다.
- 이때 데이터에 대한 Domain(분야) 전문성을 바탕으로 데이터를 합치거나 쪼개는 등을 거쳐 Feature을 만들게 된다.
- 간단한 예로 시간 데이터를 AM/PM으로 나누는 것이다.
- 이 작업은 한번 해서 끝나는 것이 아니라 끊임 없이 모델링 성능을 높이는 목적으로 반복해서 작업할 수 있는 부분이기 때문에 전문성과 경험에 따라 비용과 시간을 줄일 수 있는 부분이다.
Mapping s -> x
- states can be thought of as categorical variable
- (0,0) -> category 1
- (0,1) -> category 2
- etc
- how do we treat categorical variable? One-Hot encoding
- what if we do one-hot encoding?
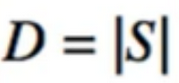
- s=(0,0) -> x=[1,0,0,..]
- s=(0,1) -> x=[0,1,0,..]
- D is the cardinality(基数) of S
- 집합의 cardinality는 집합의 원소의 개수를 말한다.
- 두 집합 A,B가 cardinal number가 같다고 함은 일대일 대응 f: A–> B가 존재하는 것이다.
- 따라서 두 집합 A,B cardinal number가 같다면 원소의 개수가 같은것이다.
- Problem with one-hot encoding: this requires the same number of parameters as measuring V(s) directly
- i.e. V is a dict with ISI keys and ISI values
- if we do one-hot encoding, each Component $θ_i$ actually represents V(s=i) itself
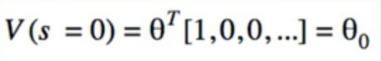
One-Hot Encoding
- one positive aspect to using one-hot encoding
- suppose our code is not working(our V isn’t accurate)
- we can have perfectly good code/no bugs, but still might not yield good results because feature are bad
- Change feature transformer to use one-hot encoding
- if it starts working, that confirm our features are bat(since it’s the same as a non-approximate method)
Alternative to One-Hot
- in case of GridWorld, each(i,j) represents a position in 2-D space
- it’s more like 2 real numbers than a category
- Vector x can be (i,j) itself
- could scale it so mean = 0 and var = 1
- this x is the “raw data”
- problem
Polynomials
- Recall from linear regression class: we can make new features by creating polynomials
- Recall from calculus: infinite taylor expansion can approximate any function
- Ex. second order terms
- $x_1$^2
- $x_2$^2
- $x_1$$x_2$
- don’t overfit
10. Approximation MC Prediction
- Replace V(s) with linear model
- there are two main steps
- With Approximation
Pseudocode
def mc_approx_prediction(π): θ = random for i = 1..N states_and_returns = play_game for s, g in states_and_returns: x = Φ(s) θ = θ + α(g-θ^T*x)x
11. Approximation TD(0)
- apply approximation to TD(0) -> but one caveat(警告)
- Main difference between MC and TD(0): instead of Using G, we use r+ɣV(s’)

- Problem
- the target is not a real target, because it require a model prediction
- Gradient is not a true gradient, so we call it a “Semi-Gradient”
- Remember don’t need to calculate returns, use rewards directly
12. Semi-Gradient SARSA
- SARSA with approximation
- we will approximate Q
- More difficult than Approximating V, Since instead of approximating ISI value, we need to approximate ISI x IAI values
- Model Prediction appears in target again, so this is another instance of semi gradient
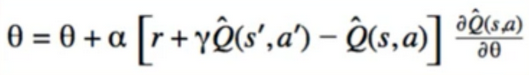
- Features
- Need to combine(s,a) -> x
- Simple Idea: take our old encoding of s(r,c,r*c) and add one-hot encoding of action
- x = (r,c,r*c,U,D,L,R,1)
- r,c is the raw and column
- it well not approximate Q well but try to find it
- Best Features
x = [ r && U, c* && U, r*r && U, c*c && U, r*c && U, l && U, r && D, ]- 6 per action x 4actions + 1bias = 25 features
- tabular method : 9states x 4actions = 36
- action value function을 Q-Table로 작성하여 푸는 방법을 Tabular Methods
- Tabular Methods를 state 나 action이 작을때만 적용 가능 하다고 한다.
- 왜냐하면 각각의 state에 action마다 Q값을 넣어줘야 하기 때문이다. 그래서 실제 환경이나 실생활, 혹은 연속적인 환경에서는 적용을 할 수 없다.
- Similar to NLP: word2idx is a dict that maps each word to a unique index in x
- SA2IDX(Semi-gradient SARSA) is a dict that maps(s,a) to a unique index in x
13. Summary
- State Space can grow too large to feasibly enumerate
- Approximation methods allow us to compress number of parameters needed
- differentiable Models are a good fit, because we can use stochastic gradient decent
- Online Learning is good because if we have a long episode, agent can learn during the episode
- Everything we learned is just as applicable to deep learning / neural nets
- x = (i,j) is not expressive enough, so we used feature engineering
- we applied approximation to:
- MC Prediction
- TD(0) Prediction(semi-Gradient)
- SARSA(Semi-Gradient)
- Why didn’t we apply approximation to Q-Learning?
- Q-learning is an off-policy method
- Sources have stated approximation for off-policy control methods do not have good convergence characteristics (utton & Barto)
- we are encouraged to modify SARSA to use Q-learning instead
- Recall: with Q-learning the a’ we use in update is not necessarily the action we will take next
- but it has been done at “Deep Q Learning”
- we’re encouraged to modify SARSA to use Q-Learning instead
Reference:
Artificial Intelligence Reinforcement Learning

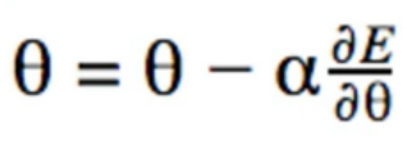
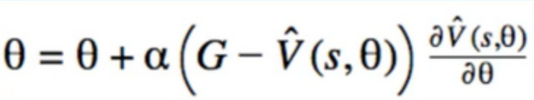
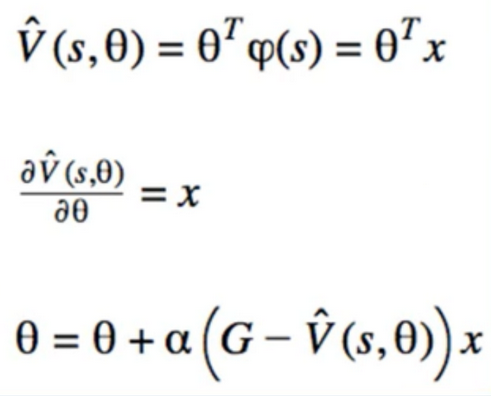
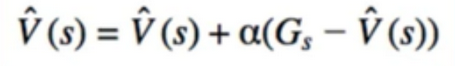
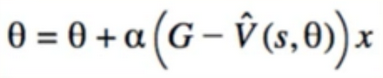
Comments