15. Review
01 Oct 2019 | Reinforcement Learning
Review
- Multi-armed bandit Review(Bayesian machine learning: A/B Testing)
- Explore-exploit dilemma
- 4 Algorithms:
- Epsilon-greedy
- Optimistic initial Value
- UCB1
- Thompson Sampling
- Basic definitions in RL
- Tic-Tac-Toe
- MDPs
- Policies state-value functions, action-value funtions
- Return
- 3 methods:
- Dynamic Programming(direct application of bellman’s Equation)
- Policy iteration, Value iteration
- Monte Carlo
- Learning from experience
- Not fully online
- Temporal Difference Learning
- Fully online with bootstrapping
- Also learn from experience
- Approximation Methods
- Tabular methods can be infeasible for large state spaces
- action value funtion을 Q-table로 작성하여 푸는 방법
- differential models(feature engineering)
1. Review of MDPs
- Markov decision Processes
- MDPs a collection of 5 things:
- set of all states
- set of all actions
- set of all rewards
- state transition probabilities
- Discount factor(gamma)
- States
- State represents what the sensors of our agent measure from the environment
- In GridWorld, that would be our position on the board
- in tic-tac-toe: specific configuration of pieces on the board
- Video game: pixel on the screen
- Maybe also : # of lives we have left, health, etc
- For an AI to be as human as possible maybe we should require it to learn that only from pixels on the screen
- Actions
- Anything the agent can do while in a state
- tic-tac-toe: placing a piece on the board
- Video game: moving up/down/left/right, pressing an action button
- Rewards
- Agent receives a reward at every time step
- reward are real-valued
- goal of agent is to maximize total future reward
- careful to define rewards the right way
- Ex. Robot trying to solve a maze receives a reward of 0 at every step and 1 for solving the maze
- possible that robot will never solve the maze, or solve it very inefficiently
- it has only experience 0 reward, thinks that is the best it can do, no incentive to not act randomly
- better solution is -1 reward at every time step
- now it has incentive to solve the maze as quickly as possible
- “Negative” and “Positive” don’t have connotations(含义) when it comes to RL agents
- just a number on a scale
- E.g -3 is better reward than -300
- been debated whether or not we should override the default rewards
- in real world environment, we would be the ones defining rewards
- State-transition probabilities
- At first glance, might seem unnecessary
- p(s’,r I s,a)
- if we do action a while in state s, won’t i always go to s?
- GridWorld: action “up”, should always take us to the square above
- Not all environments are deterministic - have a source of randomness
- reading of the state can be imperfect
- may only reflect partial knowledge
- Makrov propertys
- p[s(t+1),r(t+1)I s(t), a(t), s(t-1), a(t-1),…,(s1),a(1)]=p[s(t+1),r(t+1) I s(t), a(t)]
- as usual by “Markov” we mean first-order Markov
- A.K.a Markov assumption
- p(s’,r I s,a)
- Note: ‘ don’t mean t+1
- Discount factor
- Value Function
- State-Value and Action-Value
- When to use Q(s,a)
- Episodes
- E.g one run of tic-tac-toe
- Typically an agent will need to play many episodes to learn an optimal policy
- Tasks that end are called episodic tasks
- Tasks that last forever are called continuous task
- Terminal state - the state at which an episode ends
- Since the value function is the expected future reward after arriving in a state, the value of any terminal state is 0
2. Dynamic Programming
- Pioneered by Richard Bellman
- The bellman Equations for MDPs allow us to define the value function recursively

- if we look carefully, this is actually a linear system of equations:
- V(s1)= $a_11$V(s1) + $a_12$V(s1) + … + $a_1N$V(sN)
- V(s2)= $a_21$V(s2) + $a_22$V(s1) + … + $a_2N$V(sN)
- but since this is machine learning we are more interested in iterative solutions
- prediction problem: Given a polic, find the value function
- simply keep recalculating the right side and assign it to the left until there is no more change
- bellman’s equation says they should be equal
- one “trick” : don’t update set of V(s)’s only from previous set of V(s)’s, just update V(s) in-place -it’s faster
- Policy Iteration
- For solving the control problem
while not converged:
Step 1) Policy evaluation on current policy
Step 2) Policy Improvement (take the argmax over Q(s,a))
- Policy iteration is inefficient
- outer loop is iterative
- policy evaluation(inner loop) is also iterative
- iterative algorithm inside another
- Value Iteration
- Instead of waiting for policy evaluation to converge just do iteration
- overall it will still converge
- Furthermore, we don’t need to explicitly do the policy improvement step at all
- Since it’s the argmax, then taking the max in the policy evaluation step in equivalent
- Taking the max appears again in Q-Learning
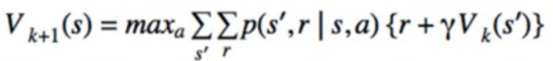
- lays the ground work, but is not very practical
- we need to loop through all state on every iteration
- state space may be very large or infinite
- requires us to know p(s’,r I s,a)
- calculating that can be infeasible
- doesn’t learn from experience
- MC and TD learning do, no model of the environment needed
3. Monte Carlo Methods(MC)
- Unlike DP, MC is all about learning from experience
- Expected values can be approximated by sample means
- Play a bund of episodes, gather returns, average them
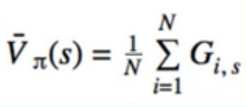
- only gives us values for states we encountered
- if we never encountered a state, its value is unknown
- what about the control problem?
- we return to the ide of policy iteration
- Montel Carlo control
- initialize random policy
- while not converged:
- play an episode, calculate returns for each state
- Do policy improvement based on current Q(s,a)(take the argmax)
- Look-ahead search with V(s) is not practical if we don’t have full control over environment, so we use Q(s,a)
- Unusual/interesting: the averaged returns are for difference policies, yet it still converged
- Problem
- MC control as given won’t always work
- requires many episodes
- what if we’re not doing an episodic task?
- what if the current policy is to bump into a wall or walk around in a circle? the episode will never end
- one solution: end the episode if we catch ourselves in a loop, give a large negative reward for that action
- Agent won’t do it again, since policy is chosen as argmax
- Another Problem
- MC can leave may states unexplored
- we had never know if going to these states is better/worse than our current policy, because we have no data on them
- one solution: the “exploring stats” method-start from a random state each episode
- requires full control over environment, not always feasible
- Another solution: epsilon-greedy
- by moving randomly with small probability epsilon, we’ll eventually explore all states sufficiently
4. Temporal difference Learning(TD)
- Unique to RL
- MC: sample returns based on an episode
- TD: estimate return based on current value function estimate
- We looked at TD(0)
- instead of using G, we use r+ɣV(s’)
- Calculating means
- basic naive way:
- collect all samples in an array, sum them, divide by N
- Major disadvantage - it requires us to store all samples in memory - space inefficient
- can calculate current sample mean from last sample mean
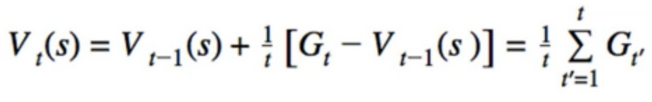
- Not only is it space efficient, it also looks curiously like gradient descent(in fact, it is ) we can Generalized it:
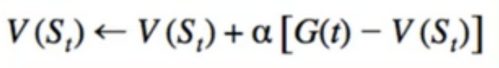
- Back to TD(0)
- TD control
Pseudocode
Q(s,a) = arbitrary, Q(terminal,a) = 0
for t=1..N
s = start_state, a = epsilon_greedy_from(Q(s))
while not game over:
s', r = do_action(a)
a' = episode_greedy_from(Q(s'))
Q(s,a) = Q(s,a) + alpha + [r + gamma*Q(s',a')-Q(s,a)]
s = s', a = q'
- Q-Learning
5. Approximation Methods
- we studied DP, MC, and TD using tabular methods
- we stored V(s) and Q(s,a) as dictionaries
- this work ok but only for small problems
- it won’t work for billion or trillion of states, and certainly not an infinite number of states
- we know that supervised learning can be used for funtion approximation
- we want to estimate V or Q
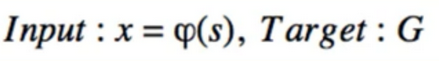
- Since reward is a real number, so is , therefore we do regression, and the appropriate loss is squared error
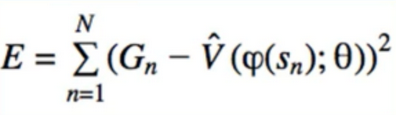
- Linear Models
- General Models
- Continuous state-spaces
- light intensity in 3-D space
- 3-D space is Continuous, light intensity is Continuous
- Continuous action-space
- Amount of force applied to a motor
- parameterized V
- parameterized π
- it called “policy gradient” method
- learned from our current experience only
- as we play, we accumulate(input, target) pairs
- E.g accumulate training data
- save these in a file and do more training
- in deep learning, we loop through the same training data multiple times (called ‘epochs’)
- No reason we can’t learn from our previous experience as well
- Replay a previous episode, update params based on old episodes
- CNNs
- RNNs
-
Regression, Classification
Reference:
Artificial Intelligence Reinforcement Learning
Review
- Multi-armed bandit Review(Bayesian machine learning: A/B Testing)
- Explore-exploit dilemma
- 4 Algorithms:
- Epsilon-greedy
- Optimistic initial Value
- UCB1
- Thompson Sampling
- Basic definitions in RL
- Tic-Tac-Toe
- MDPs
- Policies state-value functions, action-value funtions
- Return
- 3 methods:
- Dynamic Programming(direct application of bellman’s Equation)
- Policy iteration, Value iteration
- Monte Carlo
- Learning from experience
- Not fully online
- Temporal Difference Learning
- Fully online with bootstrapping
- Also learn from experience
- Dynamic Programming(direct application of bellman’s Equation)
- Approximation Methods
- Tabular methods can be infeasible for large state spaces
- action value funtion을 Q-table로 작성하여 푸는 방법
- differential models(feature engineering)
1. Review of MDPs
- Markov decision Processes
- MDPs a collection of 5 things:
- set of all states
- set of all actions
- set of all rewards
- state transition probabilities
- Discount factor(gamma)
- States
- State represents what the sensors of our agent measure from the environment
- In GridWorld, that would be our position on the board
- in tic-tac-toe: specific configuration of pieces on the board
- Video game: pixel on the screen
- Maybe also : # of lives we have left, health, etc
- For an AI to be as human as possible maybe we should require it to learn that only from pixels on the screen
- Actions
- Anything the agent can do while in a state
- tic-tac-toe: placing a piece on the board
- Video game: moving up/down/left/right, pressing an action button
- Rewards
- Agent receives a reward at every time step
- reward are real-valued
- goal of agent is to maximize total future reward
- careful to define rewards the right way
- Ex. Robot trying to solve a maze receives a reward of 0 at every step and 1 for solving the maze
- possible that robot will never solve the maze, or solve it very inefficiently
- it has only experience 0 reward, thinks that is the best it can do, no incentive to not act randomly
- better solution is -1 reward at every time step
- now it has incentive to solve the maze as quickly as possible
- “Negative” and “Positive” don’t have connotations(含义) when it comes to RL agents
- just a number on a scale
- E.g -3 is better reward than -300
- been debated whether or not we should override the default rewards
- in real world environment, we would be the ones defining rewards
- State-transition probabilities
- At first glance, might seem unnecessary
- p(s’,r I s,a)
- if we do action a while in state s, won’t i always go to s?
- GridWorld: action “up”, should always take us to the square above
- Not all environments are deterministic - have a source of randomness
- reading of the state can be imperfect
- may only reflect partial knowledge
- Makrov propertys
- p[s(t+1),r(t+1)I s(t), a(t), s(t-1), a(t-1),…,(s1),a(1)]=p[s(t+1),r(t+1) I s(t), a(t)]
- as usual by “Markov” we mean first-order Markov
- A.K.a Markov assumption
- p(s’,r I s,a)
- Note: ‘ don’t mean t+1
- Discount factor
- Value Function
- State-Value and Action-Value
- When to use Q(s,a)
- Episodes
- E.g one run of tic-tac-toe
- Typically an agent will need to play many episodes to learn an optimal policy
- Tasks that end are called episodic tasks
- Tasks that last forever are called continuous task
- Terminal state - the state at which an episode ends
- Since the value function is the expected future reward after arriving in a state, the value of any terminal state is 0
2. Dynamic Programming
- Pioneered by Richard Bellman
- The bellman Equations for MDPs allow us to define the value function recursively

- if we look carefully, this is actually a linear system of equations:
- V(s1)= $a_11$V(s1) + $a_12$V(s1) + … + $a_1N$V(sN)
- V(s2)= $a_21$V(s2) + $a_22$V(s1) + … + $a_2N$V(sN)
- but since this is machine learning we are more interested in iterative solutions
- prediction problem: Given a polic, find the value function
- simply keep recalculating the right side and assign it to the left until there is no more change
- bellman’s equation says they should be equal
- one “trick” : don’t update set of V(s)’s only from previous set of V(s)’s, just update V(s) in-place -it’s faster
- Policy Iteration
- For solving the control problem
while not converged: Step 1) Policy evaluation on current policy Step 2) Policy Improvement (take the argmax over Q(s,a)) - Policy iteration is inefficient
- outer loop is iterative
- policy evaluation(inner loop) is also iterative
- iterative algorithm inside another
- For solving the control problem
- Value Iteration
- Instead of waiting for policy evaluation to converge just do iteration
- overall it will still converge
- Furthermore, we don’t need to explicitly do the policy improvement step at all
- Since it’s the argmax, then taking the max in the policy evaluation step in equivalent
- Taking the max appears again in Q-Learning
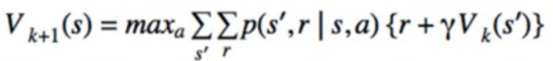
- lays the ground work, but is not very practical
- we need to loop through all state on every iteration
- state space may be very large or infinite
- requires us to know p(s’,r I s,a)
- calculating that can be infeasible
- doesn’t learn from experience
- MC and TD learning do, no model of the environment needed
3. Monte Carlo Methods(MC)
- Unlike DP, MC is all about learning from experience
- Expected values can be approximated by sample means
- Play a bund of episodes, gather returns, average them
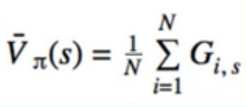
- only gives us values for states we encountered
- if we never encountered a state, its value is unknown
- what about the control problem?
- we return to the ide of policy iteration
- Montel Carlo control
- initialize random policy
- while not converged:
- play an episode, calculate returns for each state
- Do policy improvement based on current Q(s,a)(take the argmax)
- Look-ahead search with V(s) is not practical if we don’t have full control over environment, so we use Q(s,a)
- Unusual/interesting: the averaged returns are for difference policies, yet it still converged
- Problem
- MC control as given won’t always work
- requires many episodes
- what if we’re not doing an episodic task?
- what if the current policy is to bump into a wall or walk around in a circle? the episode will never end
- one solution: end the episode if we catch ourselves in a loop, give a large negative reward for that action
- Agent won’t do it again, since policy is chosen as argmax
- Another Problem
- MC can leave may states unexplored
- we had never know if going to these states is better/worse than our current policy, because we have no data on them
- one solution: the “exploring stats” method-start from a random state each episode
- requires full control over environment, not always feasible
- Another solution: epsilon-greedy
- by moving randomly with small probability epsilon, we’ll eventually explore all states sufficiently
4. Temporal difference Learning(TD)
- Unique to RL
- MC: sample returns based on an episode
- TD: estimate return based on current value function estimate
- We looked at TD(0)
- instead of using G, we use r+ɣV(s’)
- Calculating means
- basic naive way:
- collect all samples in an array, sum them, divide by N
- Major disadvantage - it requires us to store all samples in memory - space inefficient
- can calculate current sample mean from last sample mean
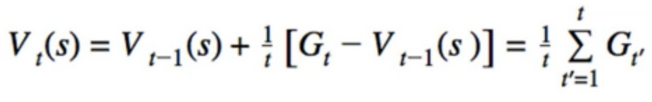
- Not only is it space efficient, it also looks curiously like gradient descent(in fact, it is ) we can Generalized it:
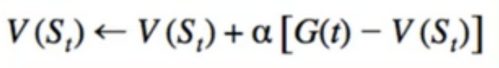
- Back to TD(0)
- TD control
Pseudocode
Q(s,a) = arbitrary, Q(terminal,a) = 0
for t=1..N
s = start_state, a = epsilon_greedy_from(Q(s))
while not game over:
s', r = do_action(a)
a' = episode_greedy_from(Q(s'))
Q(s,a) = Q(s,a) + alpha + [r + gamma*Q(s',a')-Q(s,a)]
s = s', a = q'
- Q-Learning
5. Approximation Methods
- we studied DP, MC, and TD using tabular methods
- we stored V(s) and Q(s,a) as dictionaries
- this work ok but only for small problems
- it won’t work for billion or trillion of states, and certainly not an infinite number of states
- we know that supervised learning can be used for funtion approximation
- we want to estimate V or Q
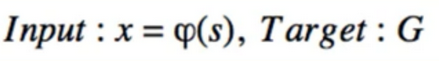
- Since reward is a real number, so is , therefore we do regression, and the appropriate loss is squared error
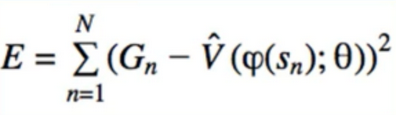
- Linear Models
- General Models
- Continuous state-spaces
- light intensity in 3-D space
- 3-D space is Continuous, light intensity is Continuous
- Continuous action-space
- Amount of force applied to a motor
- parameterized V
- parameterized π
- it called “policy gradient” method
- learned from our current experience only
- as we play, we accumulate(input, target) pairs
- E.g accumulate training data
- save these in a file and do more training
- in deep learning, we loop through the same training data multiple times (called ‘epochs’)
- No reason we can’t learn from our previous experience as well
- Replay a previous episode, update params based on old episodes
- CNNs
- RNNs
-
Regression, Classification
Reference:
Artificial Intelligence Reinforcement Learning



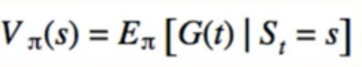
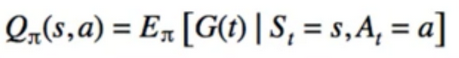
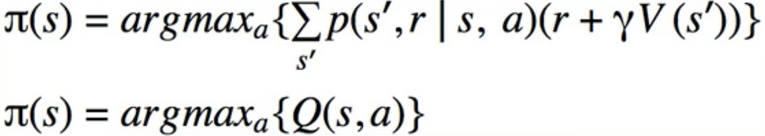
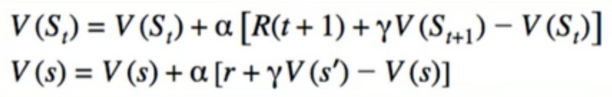
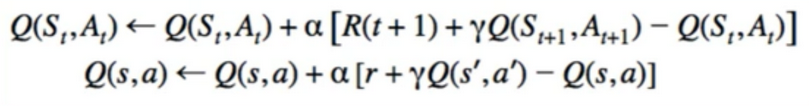
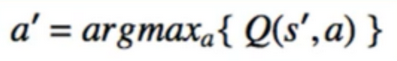
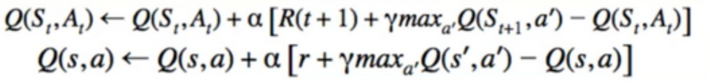
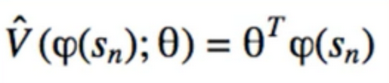
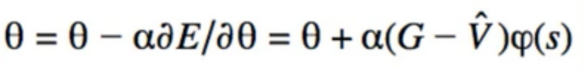
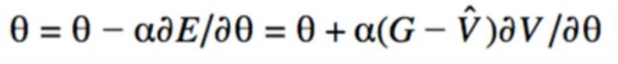
Comments