23. N-step Methods
07 Oct 2019 | Reinforcement Learning
N-step Methods
- N-step Methods : Further our understanding of TD methods
- we know so far: TD(0)
- we will learn :
- λ = 0 gives us TD(0), λ = 1 gives us monte Carlo
- any other λ is a trade-off(协调) between the two
- 1-Step TD의 step을 증가시켜 나가면서 n까지 보게 된다면 n-step TD로 일반화 할 수 있다.
- 만약 step이 무한대에 가깝게 되면 MC와 동일하게 될 것이다.
- 2-Step TD에서 업데이트 방식은 척번째 보상과 두번째 보상 그리고 부전째 상태에서의 Value function의 합으로 업데이트가 된다.
- n step TD에서의 Value 함수는 N-step 에서 얻은 총 보상에서 기존 Value 함수값과 차이를 알파만큼 가중치하여 더함으로서 업데이트가 되게 됩니다.
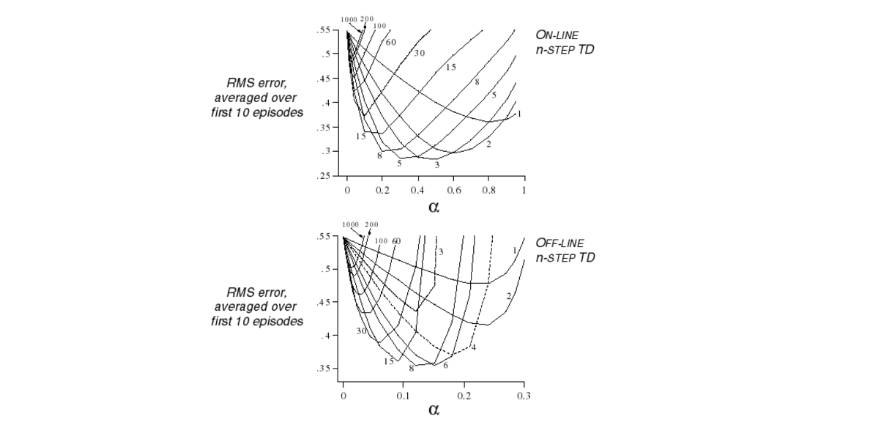
- n 이 몇일때가 가장 최고의 결과값늘 나타낼까? 위에 그래프가 실험에 대한 결과 값입니다.
- 실시간 업데이트하는 온라인 방식, 에피소드 완료후 업데이트하는 오프라인 방식에 대한 결과는 비슷하게 나온다.
- n이 커질수록 에러가 커지는 것을 볼 수 있다.
- 3~5 step 이 좋은거 같다.
- n-step 에서 보상값을 다른 값으로 평균을 낼 수 있다.
- 하지만 2~4 step에서의 평균을 내어보면 위와 같은 식이 될 것이다.
- 이 두가지를 결합하여 효율적으로 만들수 있을까?
- 답은 가능하다
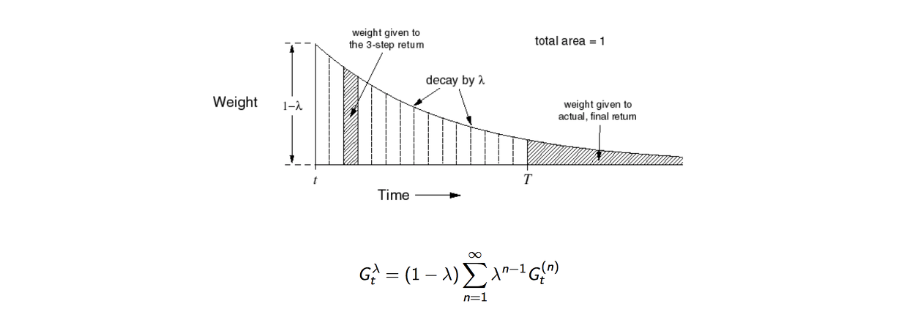
- 여기서 람다 보상은 모든 n-step 까지의 가중평균된 보상이다.
- 기존에 n-step에서 사용한 보상은 총합이였다.
- 이렇게 평균을 이용하는 방식은 오류를 더 낮출 수 있다.
- 람다의 총합이 1 되도록 하기 위해 (1-lamda)계수로 노멀라이즈를 하여 0부터 1까지의 값을 갖도록 합니다.
- 람다는 n-step이 커질 수록 보상에 대한 값을 감소시키게 합니다.
- 마지막에 공식이 TD-Lamda 의 Value 함수입니다.
- Step 시간이 흐를수록 weight가 지수형태로 감소하는 것을 볼수 있다.
- 그리고 이들의 총합은 1이 된다.
- 지수형태의 가중치 를 사용하는 것이 알고리즘 연상에 효율성을 주고 메모리를 덜 사용하게 되는 이점이 있다.
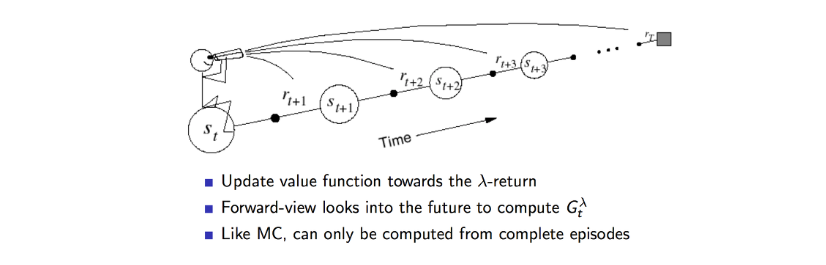
- Value 함수가 업데이트 하는 과정
- 동일하게 n-step까지 도닿라고 나서 얻은 보상들을 lamda를 이용하여 보상값을 업데이트 하게 된다.
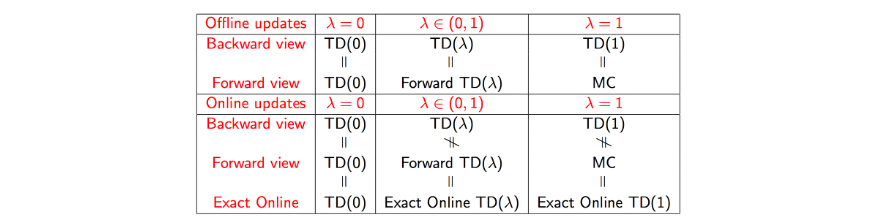
- 정방향의 관점에서 보면 이론접이다.
- 반대방향 관점에서 보면 컴퓨터 적이다.
- 반대 방향으로 보면 TD(Lamda) 알고리즘은 온라인 방식과 같이 매 step마다 업데이트가 된다.
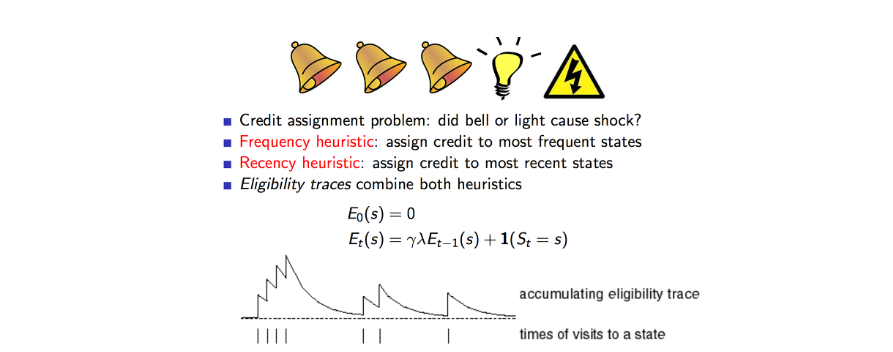
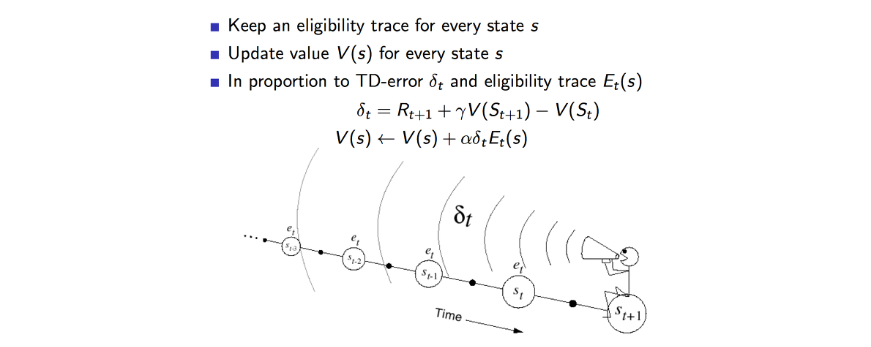
- 위에서 번개가 발생한 이유는 자주 발생한 것이 영향이 큰지 최근에 발생한 것이 영향이 큰지를 결합하여 사용할 수 있다.
- 하나의 특정한 state를 방문하는 횟수에 따라서 Eligibility Traces해보면 위에와 같이 나온다.
- 이를 적용해보면 각 state 마다 업데이트가 발생 될때 TD에러의 비율 만큼 업데이트를 가중적용하는 한다.
- 이것은 에피소드의 길이보다 짧은 기억을 하는 단기 메모리 같은 역할을 한다.
- lamda는 얼마나 빨리 값을 감소시키는가를 의미한다.
- lamda의 값이 0이 되면 완전 가파르게 decay가 발생할 것이다.
- 결국 현재 state의 value 함수만 업데이트가 되며 니는 TD(0)가 동일한 방식이 된다.
- 반대로 lamda가 1이 되면 에피소드를 모두 커버하게 된다.
- MC와 같은 방식으로 오프라인 업데이트가 된다.
- value function can be described recursively(bellman’s equation)
- we can estimate V by taking the sample mean of G’s
- TD(0) is to combine these 2 things to estimate G itself(all we know for sure is r)
- All we know for sure is R
- it’s plausible(有道理的) to ask: what if we use more r’s and less of V?
- Monte Carlo is just the extreme of this, where we don’t use V at all
- Let’s superscript G to tell us how many R’s we are using
- gives us a discrete transition from TD(0) to Monte Carlo
- TD(0) - wait 1 step to update V
- Monte Carlo - Wait until end of episode to update V
- N-step -wait N step to update V
- why? we need to collect all the R’s
- For the actual update(which is in terms of G already). no change is needed
- the only change is to G itself
Control
- Use Q instead of V
- Ex. SARSA
Code
# https://deeplearningcourses.com/c/deep-reinforcement-learning-in-python
# https://www.udemy.com/deep-reinforcement-learning-in-python
from __future__ import print_function, division
from builtins import range
# Note: you may need to update your version of future
# sudo pip install -U future
#
# Note: gym changed from version 0.7.3 to 0.8.0
# MountainCar episode length is capped at 200 in later versions.
# This means your agent can't learn as much in the earlier episodes
# since they are no longer as long.
#
# Adapt Q-Learning script to use N-step method instead
import gym
import os
import sys
import numpy as np
import matplotlib.pyplot as plt
from gym import wrappers
from datetime import datetime
# code we already wrote
import q_learning
from q_learning import plot_cost_to_go, FeatureTransformer, Model, plot_running_avg
SGDRegressor
class SGDRegressor:
def __init__(self, **kwargs):
self.w = None
self.lr = 1e-2
def partial_fit(self, X, Y):
if self.w is None:
D = X.shape[1]
self.w = np.random.randn(D) / np.sqrt(D)
self.w += self.lr*(Y - X.dot(self.w)).dot(X)
def predict(self, X):
return X.dot(self.w)
# replace SKLearn Regressor
q_learning.SGDRegressor = SGDRegressor
# calculate everything up to max[Q(s,a)]
# Ex.
# R(t) + gamma*R(t+1) + ... + (gamma^(n-1))*R(t+n-1) + (gamma^n)*max[Q(s(t+n), a(t+n))]
# def calculate_return_before_prediction(rewards, gamma):
# ret = 0
# for r in reversed(rewards[1:]):
# ret += r + gamma*ret
# ret += rewards[0]
# return ret
play
# returns a list of states_and_rewards, and the total reward
def play_one(model, eps, gamma, n=5):
# n is n-step
observation = env.reset()
done = False
totalreward = 0
rewards = []
states = []
actions = []
iters = 0
# array of [gamma^0, gamma^1, ..., gamma^(n-1)]
multiplier = np.array([gamma]*n)**np.arange(n)
# while not done and iters < 200:
while not done and iters < 10000:
# in earlier versions of gym, episode doesn't automatically
# end when you hit 200 steps
action = model.sample_action(observation, eps)
states.append(observation)
actions.append(action)
prev_observation = observation
observation, reward, done, info = env.step(action)
rewards.append(reward)
# update the model
if len(rewards) >= n:
# return_up_to_prediction = calculate_return_before_prediction(rewards, gamma)
return_up_to_prediction = multiplier.dot(rewards[-n:])
G = return_up_to_prediction + (gamma**n)*np.max(model.predict(observation)[0])
model.update(states[-n], actions[-n], G)
# if len(rewards) > n:
# rewards.pop(0)
# states.pop(0)
# actions.pop(0)
# assert(len(rewards) <= n)
totalreward += reward
iters += 1
# empty the cache
if n == 1:
rewards = []
states = []
actions = []
else:
rewards = rewards[-n+1:]
states = states[-n+1:]
actions = actions[-n+1:]
# unfortunately, new version of gym cuts you off at 200 steps
# even if you haven't reached the goal.
# it's not good to do this UNLESS you've reached the goal.
# we are "really done" if position >= 0.5
if observation[0] >= 0.5:
# we actually made it to the goal
# print("made it!")
while len(rewards) > 0:
G = multiplier[:len(rewards)].dot(rewards)
model.update(states[0], actions[0], G)
rewards.pop(0)
states.pop(0)
actions.pop(0)
else:
# we did not make it to the goal
# print("didn't make it...")
while len(rewards) > 0:
guess_rewards = rewards + [-1]*(n - len(rewards))
G = multiplier.dot(guess_rewards)
model.update(states[0], actions[0], G)
rewards.pop(0)
states.pop(0)
actions.pop(0)
return totalreward
main
if __name__ == '__main__':
env = gym.make('MountainCar-v0')
ft = FeatureTransformer(env)
model = Model(env, ft, "constant")
gamma = 0.99
if 'monitor' in sys.argv:
filename = os.path.basename(__file__).split('.')[0]
monitor_dir = './' + filename + '_' + str(datetime.now())
env = wrappers.Monitor(env, monitor_dir)
N = 300
totalrewards = np.empty(N)
costs = np.empty(N)
for n in range(N):
# eps = 1.0/(0.1*n+1)
eps = 0.1*(0.97**n)
totalreward = play_one(model, eps, gamma)
totalrewards[n] = totalreward
print("episode:", n, "total reward:", totalreward)
print("avg reward for last 100 episodes:", totalrewards[-100:].mean())
print("total steps:", -totalrewards.sum())
plt.plot(totalrewards)
plt.title("Rewards")
plt.show()
plot_running_avg(totalrewards)
# plot the optimal state-value function
plot_cost_to_go(env, model)
Reference:
Artificial Intelligence Reinforcement Learning
N-step Methods
- N-step Methods : Further our understanding of TD methods
- we know so far: TD(0)
- we will learn :
- λ = 0 gives us TD(0), λ = 1 gives us monte Carlo
- any other λ is a trade-off(协调) between the two
- 1-Step TD의 step을 증가시켜 나가면서 n까지 보게 된다면 n-step TD로 일반화 할 수 있다.
- 만약 step이 무한대에 가깝게 되면 MC와 동일하게 될 것이다.
- 2-Step TD에서 업데이트 방식은 척번째 보상과 두번째 보상 그리고 부전째 상태에서의 Value function의 합으로 업데이트가 된다.
- n step TD에서의 Value 함수는 N-step 에서 얻은 총 보상에서 기존 Value 함수값과 차이를 알파만큼 가중치하여 더함으로서 업데이트가 되게 됩니다.
- n 이 몇일때가 가장 최고의 결과값늘 나타낼까? 위에 그래프가 실험에 대한 결과 값입니다.
- 실시간 업데이트하는 온라인 방식, 에피소드 완료후 업데이트하는 오프라인 방식에 대한 결과는 비슷하게 나온다.
- n이 커질수록 에러가 커지는 것을 볼 수 있다.
- 3~5 step 이 좋은거 같다.
- n-step 에서 보상값을 다른 값으로 평균을 낼 수 있다.
- 하지만 2~4 step에서의 평균을 내어보면 위와 같은 식이 될 것이다.
- 이 두가지를 결합하여 효율적으로 만들수 있을까?
- 답은 가능하다
- 여기서 람다 보상은 모든 n-step 까지의 가중평균된 보상이다.
- 기존에 n-step에서 사용한 보상은 총합이였다.
- 이렇게 평균을 이용하는 방식은 오류를 더 낮출 수 있다.
- 람다의 총합이 1 되도록 하기 위해 (1-lamda)계수로 노멀라이즈를 하여 0부터 1까지의 값을 갖도록 합니다.
- 람다는 n-step이 커질 수록 보상에 대한 값을 감소시키게 합니다.
- 마지막에 공식이 TD-Lamda 의 Value 함수입니다.
- Step 시간이 흐를수록 weight가 지수형태로 감소하는 것을 볼수 있다.
- 그리고 이들의 총합은 1이 된다.
- 지수형태의 가중치 를 사용하는 것이 알고리즘 연상에 효율성을 주고 메모리를 덜 사용하게 되는 이점이 있다.
- Value 함수가 업데이트 하는 과정
- 동일하게 n-step까지 도닿라고 나서 얻은 보상들을 lamda를 이용하여 보상값을 업데이트 하게 된다.
- 정방향의 관점에서 보면 이론접이다.
- 반대방향 관점에서 보면 컴퓨터 적이다.
- 반대 방향으로 보면 TD(Lamda) 알고리즘은 온라인 방식과 같이 매 step마다 업데이트가 된다.
- 위에서 번개가 발생한 이유는 자주 발생한 것이 영향이 큰지 최근에 발생한 것이 영향이 큰지를 결합하여 사용할 수 있다.
- 하나의 특정한 state를 방문하는 횟수에 따라서 Eligibility Traces해보면 위에와 같이 나온다.
- 이를 적용해보면 각 state 마다 업데이트가 발생 될때 TD에러의 비율 만큼 업데이트를 가중적용하는 한다.
- 이것은 에피소드의 길이보다 짧은 기억을 하는 단기 메모리 같은 역할을 한다.
- lamda는 얼마나 빨리 값을 감소시키는가를 의미한다.
- lamda의 값이 0이 되면 완전 가파르게 decay가 발생할 것이다.
- 결국 현재 state의 value 함수만 업데이트가 되며 니는 TD(0)가 동일한 방식이 된다.
- 반대로 lamda가 1이 되면 에피소드를 모두 커버하게 된다.
- MC와 같은 방식으로 오프라인 업데이트가 된다.
- value function can be described recursively(bellman’s equation)
- we can estimate V by taking the sample mean of G’s
- TD(0) is to combine these 2 things to estimate G itself(all we know for sure is r)
- All we know for sure is R
- it’s plausible(有道理的) to ask: what if we use more r’s and less of V?
- Monte Carlo is just the extreme of this, where we don’t use V at all
- Let’s superscript G to tell us how many R’s we are using
- gives us a discrete transition from TD(0) to Monte Carlo
- TD(0) - wait 1 step to update V
- Monte Carlo - Wait until end of episode to update V
- N-step -wait N step to update V
- why? we need to collect all the R’s
- For the actual update(which is in terms of G already). no change is needed
- the only change is to G itself
Control
- Use Q instead of V
- Ex. SARSA
Code
# https://deeplearningcourses.com/c/deep-reinforcement-learning-in-python
# https://www.udemy.com/deep-reinforcement-learning-in-python
from __future__ import print_function, division
from builtins import range
# Note: you may need to update your version of future
# sudo pip install -U future
#
# Note: gym changed from version 0.7.3 to 0.8.0
# MountainCar episode length is capped at 200 in later versions.
# This means your agent can't learn as much in the earlier episodes
# since they are no longer as long.
#
# Adapt Q-Learning script to use N-step method instead
import gym
import os
import sys
import numpy as np
import matplotlib.pyplot as plt
from gym import wrappers
from datetime import datetime
# code we already wrote
import q_learning
from q_learning import plot_cost_to_go, FeatureTransformer, Model, plot_running_avg
SGDRegressor
class SGDRegressor:
def __init__(self, **kwargs):
self.w = None
self.lr = 1e-2
def partial_fit(self, X, Y):
if self.w is None:
D = X.shape[1]
self.w = np.random.randn(D) / np.sqrt(D)
self.w += self.lr*(Y - X.dot(self.w)).dot(X)
def predict(self, X):
return X.dot(self.w)
# replace SKLearn Regressor
q_learning.SGDRegressor = SGDRegressor
# calculate everything up to max[Q(s,a)]
# Ex.
# R(t) + gamma*R(t+1) + ... + (gamma^(n-1))*R(t+n-1) + (gamma^n)*max[Q(s(t+n), a(t+n))]
# def calculate_return_before_prediction(rewards, gamma):
# ret = 0
# for r in reversed(rewards[1:]):
# ret += r + gamma*ret
# ret += rewards[0]
# return ret
play
# returns a list of states_and_rewards, and the total reward
def play_one(model, eps, gamma, n=5):
# n is n-step
observation = env.reset()
done = False
totalreward = 0
rewards = []
states = []
actions = []
iters = 0
# array of [gamma^0, gamma^1, ..., gamma^(n-1)]
multiplier = np.array([gamma]*n)**np.arange(n)
# while not done and iters < 200:
while not done and iters < 10000:
# in earlier versions of gym, episode doesn't automatically
# end when you hit 200 steps
action = model.sample_action(observation, eps)
states.append(observation)
actions.append(action)
prev_observation = observation
observation, reward, done, info = env.step(action)
rewards.append(reward)
# update the model
if len(rewards) >= n:
# return_up_to_prediction = calculate_return_before_prediction(rewards, gamma)
return_up_to_prediction = multiplier.dot(rewards[-n:])
G = return_up_to_prediction + (gamma**n)*np.max(model.predict(observation)[0])
model.update(states[-n], actions[-n], G)
# if len(rewards) > n:
# rewards.pop(0)
# states.pop(0)
# actions.pop(0)
# assert(len(rewards) <= n)
totalreward += reward
iters += 1
# empty the cache
if n == 1:
rewards = []
states = []
actions = []
else:
rewards = rewards[-n+1:]
states = states[-n+1:]
actions = actions[-n+1:]
# unfortunately, new version of gym cuts you off at 200 steps
# even if you haven't reached the goal.
# it's not good to do this UNLESS you've reached the goal.
# we are "really done" if position >= 0.5
if observation[0] >= 0.5:
# we actually made it to the goal
# print("made it!")
while len(rewards) > 0:
G = multiplier[:len(rewards)].dot(rewards)
model.update(states[0], actions[0], G)
rewards.pop(0)
states.pop(0)
actions.pop(0)
else:
# we did not make it to the goal
# print("didn't make it...")
while len(rewards) > 0:
guess_rewards = rewards + [-1]*(n - len(rewards))
G = multiplier.dot(guess_rewards)
model.update(states[0], actions[0], G)
rewards.pop(0)
states.pop(0)
actions.pop(0)
return totalreward
main
if __name__ == '__main__':
env = gym.make('MountainCar-v0')
ft = FeatureTransformer(env)
model = Model(env, ft, "constant")
gamma = 0.99
if 'monitor' in sys.argv:
filename = os.path.basename(__file__).split('.')[0]
monitor_dir = './' + filename + '_' + str(datetime.now())
env = wrappers.Monitor(env, monitor_dir)
N = 300
totalrewards = np.empty(N)
costs = np.empty(N)
for n in range(N):
# eps = 1.0/(0.1*n+1)
eps = 0.1*(0.97**n)
totalreward = play_one(model, eps, gamma)
totalrewards[n] = totalreward
print("episode:", n, "total reward:", totalreward)
print("avg reward for last 100 episodes:", totalrewards[-100:].mean())
print("total steps:", -totalrewards.sum())
plt.plot(totalrewards)
plt.title("Rewards")
plt.show()
plot_running_avg(totalrewards)
# plot the optimal state-value function
plot_cost_to_go(env, model)
Reference:
Artificial Intelligence Reinforcement Learning







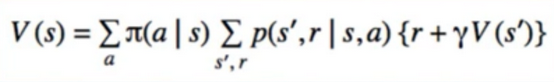
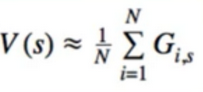

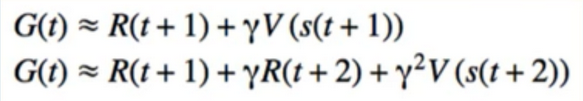
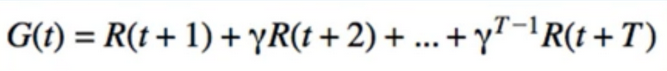
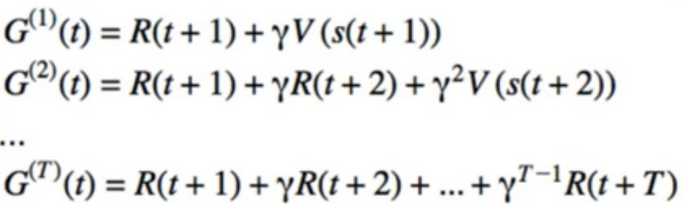
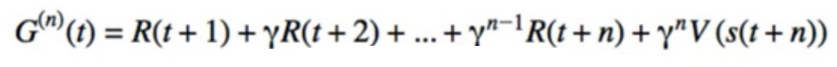
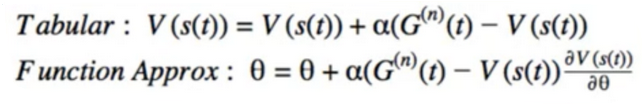
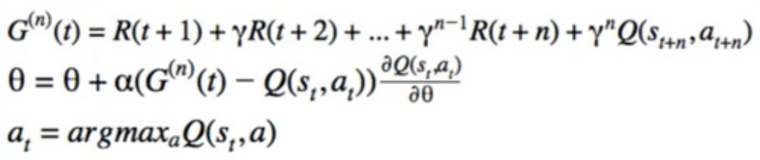
Comments