24. TD LAMDA
08 Oct 2019 | Reinforcement Learning
TD(λ)
- Generalize N-step method
- λ is associated with something called the []”eligibility trace”(전격 흔적)](https://sumniya.tistory.com/14)
- eligibility trace라는 개념 : 이는 과거에 방문했던 state 중에서 현재 얻게 되는 reward에 영향을 주는 state를 판단하여, 현재 얻게 되는 reward을 해당 state에 나누어주는 것입니다. 이때, 영향을 주었다고 판단하는 index를 credit이라고하고 이 credit을 assign할 때, 두 가지 기준을 씁니다. 1) Frequency heuristic(얼마나 자주 방문했는가?) 2) Recency heuristic(얼마나 최근에 방문 했는가?)
- N-step method code is complicated - not trivial to keep track of all rewards(then flush them once episode is over)
- TD(λ) allows us a more elegant method to trade-off between TD(0) and MC
- can update after just 1 step
- λ = 0 gives us TD(0), λ=1 gives us Monte Carlo
N-step method
- Recall:
- strange idea: combine these :
TD(λ)
- let’s take this strangeness to the next level - let’s combine more G’s, even an infinite number of G’s
- λ must sum to 1 so that the result is on the same scale as individual G’s
- in TD(λ). we make the coefficients decrease geometrically
- Problem: these don’t sum to 1
- we are most interested in the case when n - > ∞
- we know this from calculus:
- therefore, we should scale the sum by thins amount
- we call this the **
- we assume our episode will end at some point(say, time step T)
- when we reach step T - t, the episode is over, so any N-step return beyond this is the Full MC return, G(t)
- separate the partial N-step returns and the full returns
- manipulate 2nd term to simplify the sum
- simplify further
- when λ=0, we get the TD(0) return since $0^0$ = 1
- when λ=1, we get the full return(MC)
- any λ between 0 and 1 gives us a combination of individual returns(with geometrically decreasing weight)
- isn’t this much more computational effort than both MC and N-step methods?
- yes, we would need to calculate G(t), $G^1$(t),…,$G^t$(t)
- lots of work (benefit is not clear)
- the algorithm we’re about to learn is an approximation to calculate the true λ-return(since that would be computationally infeasible)
TD(0)
- let’s go back to TD(0) for a moment
- we call target - prediction the TD error
- parameter update is still gradient descent
- Eligibility trace is a vector the same size as parameter vector:
- Eligibility Trace/ vector keeps track of old gradients, much like momentum from deep learning
- λ tell us “how much” of the past we want to keep
- $e_0$ = 0, $e_t$ = $∇0$V($s_t$) + ɣλe(t_1)
back to TD(λ)
- redefine the parameter update to use e instead of only gradient
- recall how momentum works
- update only depends on next state
- we can do updates in 1 step rather than waiting N steps
- but still, just an approximation to using true λ-return
- N-step method and true λ-return require waiting for future rewards
- we call this the “forward view”
- in TD(λ), we update the current param based on past errors
- we call this the “backward view”
Code
# https://deeplearningcourses.com/c/deep-reinforcement-learning-in-python
# https://www.udemy.com/deep-reinforcement-learning-in-python
from __future__ import print_function, division
from builtins import range
# Note: you may need to update your version of future
# sudo pip install -U future
#
# Note: gym changed from version 0.7.3 to 0.8.0
# MountainCar episode length is capped at 200 in later versions.
# This means your agent can't learn as much in the earlier episodes
# since they are no longer as long.
#
# Adapt Q-Learning script to use TD(lambda) method instead
import gym
import os
import sys
import numpy as np
import matplotlib.pyplot as plt
from gym import wrappers
from datetime import datetime
# code we already wrote
from q_learning import plot_cost_to_go, FeatureTransformer, plot_running_avg
Base model
class BaseModel:
# this is eligience traces
def __init__(self, D):
self.w = np.random.randn(D) / np.sqrt(D)
def partial_fit(self, input_, target, eligibility, lr=1e-2):
self.w += lr*(target - input_.dot(self.w))*eligibility
def predict(self, X):
X = np.array(X)
return X.dot(self.w)
model
# Holds one BaseModel for each action
class Model:
def __init__(self, env, feature_transformer):
self.env = env
self.models = []
self.feature_transformer = feature_transformer
D = feature_transformer.dimensions # 2000 D
self.eligibilities = np.zeros((env.action_space.n, D))
for i in range(env.action_space.n):
model = BaseModel(D)
self.models.append(model)
def predict(self, s):
X = self.feature_transformer.transform([s])
assert(len(X.shape) == 2)
result = np.stack([m.predict(X) for m in self.models]).T
assert(len(result.shape) == 2)
return result
def update(self, s, a, G, gamma, lambda_):
X = self.feature_transformer.transform([s])
assert(len(X.shape) == 2)
self.eligibilities *= gamma*lambda_
self.eligibilities[a] += X[0]
self.models[a].partial_fit(X[0], G, self.eligibilities[a])
def sample_action(self, s, eps):
if np.random.random() < eps:
return self.env.action_space.sample()
else:
return np.argmax(self.predict(s))
play
# returns a list of states_and_rewards, and the total reward
def play_one(model, env, eps, gamma, lambda_):
observation = env.reset()
done = False
totalreward = 0
iters = 0
# while not done and iters < 200:
while not done and iters < 10000:
action = model.sample_action(observation, eps)
prev_observation = observation
observation, reward, done, info = env.step(action)
# update the model
next = model.predict(observation)
assert(next.shape == (1, env.action_space.n))
G = reward + gamma*np.max(next[0])
model.update(prev_observation, action, G, gamma, lambda_)
totalreward += reward
iters += 1
return totalreward
main
if __name__ == '__main__':
env = gym.make('MountainCar-v0')
ft = FeatureTransformer(env)
model = Model(env, ft)
gamma = 0.9999
lambda_ = 0.7
if 'monitor' in sys.argv:
filename = os.path.basename(__file__).split('.')[0]
monitor_dir = './' + filename + '_' + str(datetime.now())
env = wrappers.Monitor(env, monitor_dir)
N = 300
totalrewards = np.empty(N)
costs = np.empty(N)
for n in range(N):
# eps = 1.0/(0.1*n+1)
eps = 0.1*(0.97**n)
# eps = 0.5/np.sqrt(n+1)
totalreward = play_one(model, env, eps, gamma, lambda_)
totalrewards[n] = totalreward
# print("episode:", n, "total reward:", totalreward)
print("avg reward for last 100 episodes:", totalrewards[-100:].mean())
print("total steps:", -totalrewards.sum())
plt.plot(totalrewards)
plt.title("Rewards")
plt.show()
plot_running_avg(totalrewards)
# plot the optimal state-value function
plot_cost_to_go(env, model)
TD LAMDA summary
- we learned techniques that can be applied anywhere we would use Qlearning or SARSA
- general tools that we can test in a variety of situations
- “technically” got more practice with RBF networks too
N-step Methods
- we saw how N-step methods provide a “bridge” between TD(0) and MC
- we saw that we can combine all the N-step returns
- this gives us the λ-return
- we saw that λ=0 gives us TD(0). λ=1 gives us MC
Eligibility Traces
- we looked at the use of eligibility traces to approximate TD(λ) using the true λ-return(since actually calculating it would be lots of effort)
- we saw that it looks a lot like deep learning momentum
- new tools for our toolbox
- not guaranteed that any particular algorithm will work for our problem, but more tools = more thing to try
```
Reference:
Artificial Intelligence Reinforcement Learning
TD(λ)
- Generalize N-step method
- λ is associated with something called the []”eligibility trace”(전격 흔적)](https://sumniya.tistory.com/14)
- eligibility trace라는 개념 : 이는 과거에 방문했던 state 중에서 현재 얻게 되는 reward에 영향을 주는 state를 판단하여, 현재 얻게 되는 reward을 해당 state에 나누어주는 것입니다. 이때, 영향을 주었다고 판단하는 index를 credit이라고하고 이 credit을 assign할 때, 두 가지 기준을 씁니다. 1) Frequency heuristic(얼마나 자주 방문했는가?) 2) Recency heuristic(얼마나 최근에 방문 했는가?)
- N-step method code is complicated - not trivial to keep track of all rewards(then flush them once episode is over)
- TD(λ) allows us a more elegant method to trade-off between TD(0) and MC
- can update after just 1 step
- λ = 0 gives us TD(0), λ=1 gives us Monte Carlo
N-step method
- Recall:
- strange idea: combine these :
TD(λ)
- let’s take this strangeness to the next level - let’s combine more G’s, even an infinite number of G’s
- λ must sum to 1 so that the result is on the same scale as individual G’s
- in TD(λ). we make the coefficients decrease geometrically
- Problem: these don’t sum to 1
- we are most interested in the case when n - > ∞
- we know this from calculus:
- therefore, we should scale the sum by thins amount
- we call this the **
- we assume our episode will end at some point(say, time step T)
- when we reach step T - t, the episode is over, so any N-step return beyond this is the Full MC return, G(t)
- separate the partial N-step returns and the full returns
- manipulate 2nd term to simplify the sum
- simplify further
- when λ=0, we get the TD(0) return since $0^0$ = 1
- when λ=1, we get the full return(MC)
- any λ between 0 and 1 gives us a combination of individual returns(with geometrically decreasing weight)
- isn’t this much more computational effort than both MC and N-step methods?
- yes, we would need to calculate G(t), $G^1$(t),…,$G^t$(t)
- lots of work (benefit is not clear)
- the algorithm we’re about to learn is an approximation to calculate the true λ-return(since that would be computationally infeasible)
TD(0)
- let’s go back to TD(0) for a moment
- we call target - prediction the TD error
- parameter update is still gradient descent
- Eligibility trace is a vector the same size as parameter vector:
- Eligibility Trace/ vector keeps track of old gradients, much like momentum from deep learning
- λ tell us “how much” of the past we want to keep
- $e_0$ = 0, $e_t$ = $∇0$V($s_t$) + ɣλe(t_1)
back to TD(λ)
- redefine the parameter update to use e instead of only gradient
- recall how momentum works
- update only depends on next state
- we can do updates in 1 step rather than waiting N steps
- but still, just an approximation to using true λ-return
- N-step method and true λ-return require waiting for future rewards
- we call this the “forward view”
- in TD(λ), we update the current param based on past errors
- we call this the “backward view”
Code
# https://deeplearningcourses.com/c/deep-reinforcement-learning-in-python
# https://www.udemy.com/deep-reinforcement-learning-in-python
from __future__ import print_function, division
from builtins import range
# Note: you may need to update your version of future
# sudo pip install -U future
#
# Note: gym changed from version 0.7.3 to 0.8.0
# MountainCar episode length is capped at 200 in later versions.
# This means your agent can't learn as much in the earlier episodes
# since they are no longer as long.
#
# Adapt Q-Learning script to use TD(lambda) method instead
import gym
import os
import sys
import numpy as np
import matplotlib.pyplot as plt
from gym import wrappers
from datetime import datetime
# code we already wrote
from q_learning import plot_cost_to_go, FeatureTransformer, plot_running_avg
Base model
class BaseModel:
# this is eligience traces
def __init__(self, D):
self.w = np.random.randn(D) / np.sqrt(D)
def partial_fit(self, input_, target, eligibility, lr=1e-2):
self.w += lr*(target - input_.dot(self.w))*eligibility
def predict(self, X):
X = np.array(X)
return X.dot(self.w)
model
# Holds one BaseModel for each action
class Model:
def __init__(self, env, feature_transformer):
self.env = env
self.models = []
self.feature_transformer = feature_transformer
D = feature_transformer.dimensions # 2000 D
self.eligibilities = np.zeros((env.action_space.n, D))
for i in range(env.action_space.n):
model = BaseModel(D)
self.models.append(model)
def predict(self, s):
X = self.feature_transformer.transform([s])
assert(len(X.shape) == 2)
result = np.stack([m.predict(X) for m in self.models]).T
assert(len(result.shape) == 2)
return result
def update(self, s, a, G, gamma, lambda_):
X = self.feature_transformer.transform([s])
assert(len(X.shape) == 2)
self.eligibilities *= gamma*lambda_
self.eligibilities[a] += X[0]
self.models[a].partial_fit(X[0], G, self.eligibilities[a])
def sample_action(self, s, eps):
if np.random.random() < eps:
return self.env.action_space.sample()
else:
return np.argmax(self.predict(s))
play
# returns a list of states_and_rewards, and the total reward
def play_one(model, env, eps, gamma, lambda_):
observation = env.reset()
done = False
totalreward = 0
iters = 0
# while not done and iters < 200:
while not done and iters < 10000:
action = model.sample_action(observation, eps)
prev_observation = observation
observation, reward, done, info = env.step(action)
# update the model
next = model.predict(observation)
assert(next.shape == (1, env.action_space.n))
G = reward + gamma*np.max(next[0])
model.update(prev_observation, action, G, gamma, lambda_)
totalreward += reward
iters += 1
return totalreward
main
if __name__ == '__main__':
env = gym.make('MountainCar-v0')
ft = FeatureTransformer(env)
model = Model(env, ft)
gamma = 0.9999
lambda_ = 0.7
if 'monitor' in sys.argv:
filename = os.path.basename(__file__).split('.')[0]
monitor_dir = './' + filename + '_' + str(datetime.now())
env = wrappers.Monitor(env, monitor_dir)
N = 300
totalrewards = np.empty(N)
costs = np.empty(N)
for n in range(N):
# eps = 1.0/(0.1*n+1)
eps = 0.1*(0.97**n)
# eps = 0.5/np.sqrt(n+1)
totalreward = play_one(model, env, eps, gamma, lambda_)
totalrewards[n] = totalreward
# print("episode:", n, "total reward:", totalreward)
print("avg reward for last 100 episodes:", totalrewards[-100:].mean())
print("total steps:", -totalrewards.sum())
plt.plot(totalrewards)
plt.title("Rewards")
plt.show()
plot_running_avg(totalrewards)
# plot the optimal state-value function
plot_cost_to_go(env, model)
TD LAMDA summary
- we learned techniques that can be applied anywhere we would use Qlearning or SARSA
- general tools that we can test in a variety of situations
- “technically” got more practice with RBF networks too
N-step Methods
- we saw how N-step methods provide a “bridge” between TD(0) and MC
- we saw that we can combine all the N-step returns
- this gives us the λ-return
- we saw that λ=0 gives us TD(0). λ=1 gives us MC
Eligibility Traces
- we looked at the use of eligibility traces to approximate TD(λ) using the true λ-return(since actually calculating it would be lots of effort)
- we saw that it looks a lot like deep learning momentum
- new tools for our toolbox
- not guaranteed that any particular algorithm will work for our problem, but more tools = more thing to try
``` Reference:
Artificial Intelligence Reinforcement Learning

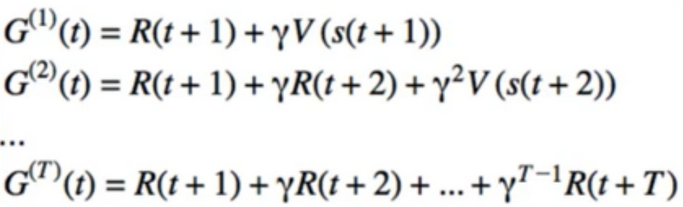
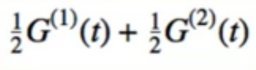

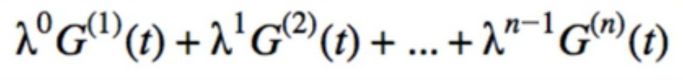
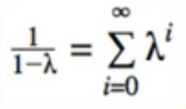
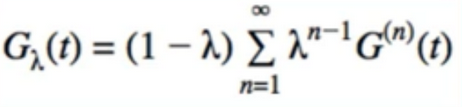
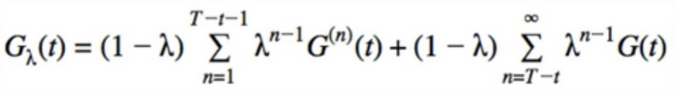
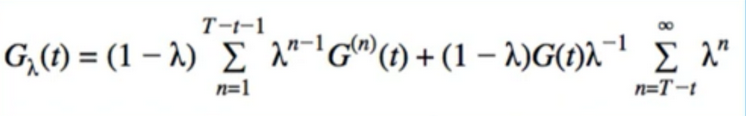
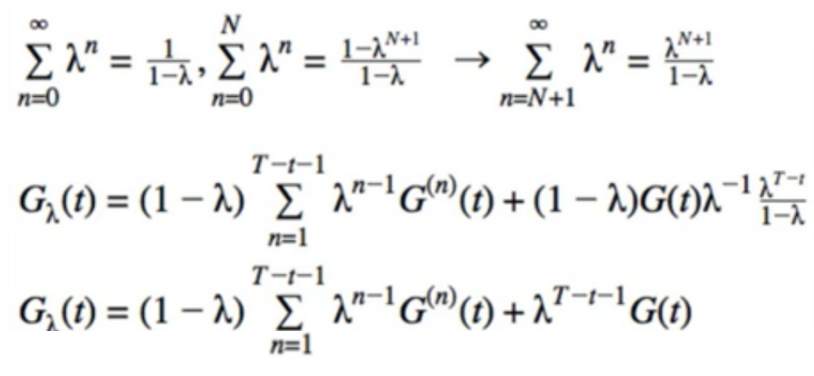
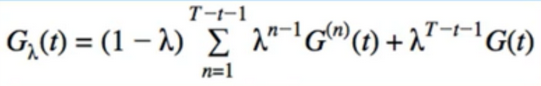
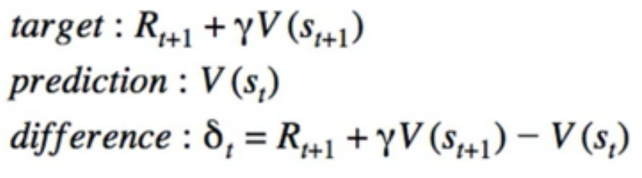
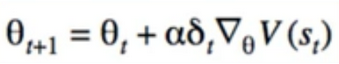

Comments