Multi-Agent path finding(MAPF) & Search algorithm
26 Sep 2019 | ROBOTICS
Multi-Agent path finding(MAPF)
- Multi-Agent(many robot) play to find the target position and move
- MAPF problem: Find a collision-free plan(path) for each agent
- Another name we called it : Cooperative path finding(CPF), Multi-robot path planning, pebble(鹅卵石) motion
1) Introduction to MAPF
- a graph (directed or undirected)
- a set of agents(robot), each agent is assigned to two locations(nodes) in the graph(start, destination)
- Each agent can perform either move(to a neighbouring node) or wait(in the same node) actions
Typical Assumption:
all move and wait actions have identical durations(plans for agents are synchronized)
- Plan is a sequence of actions for the agent leading from its start location to its destination
- the length of plan(for an agent) is defined by the time when the agent reaches its destination and does not leave it anymore.
- Find Plans for all agents such that the plans do not collide in time and space (no two agents are at the same location at the same time)
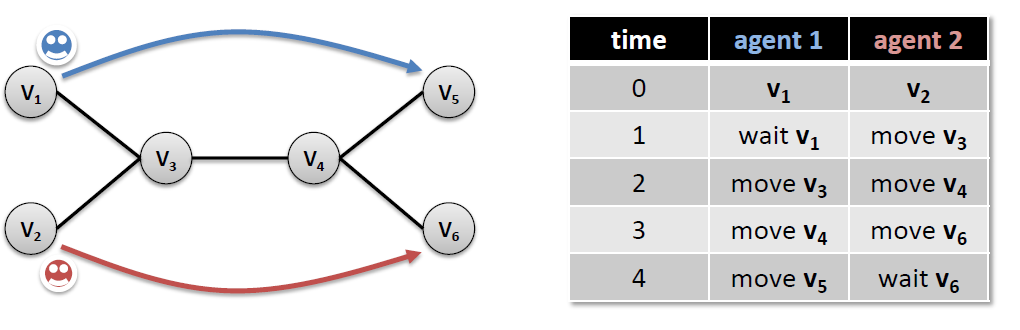
- some necessary conditions for plan existence:
- no two agents are at the same start node
- no two agents share the same destination node(unless an agent disappears when reaching its destination)
- the number of agents is strictly smaller than the number of nodes
- agent at $v_i$ cannot perform move $v_j$ at the same time when agent at $v_j$ perform move $v_i$
- Agents may swap position. but agents use the same edges at the same time, swap is not allowed
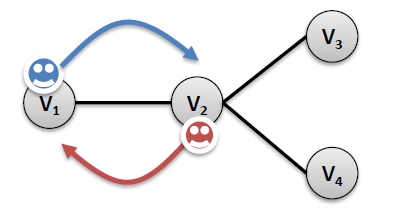
- Agent can approach node that is currently occupied but will be free before arrival(Agent at $v_i$ cannot perform move $v_j$ if there is another agent at $v_j$)
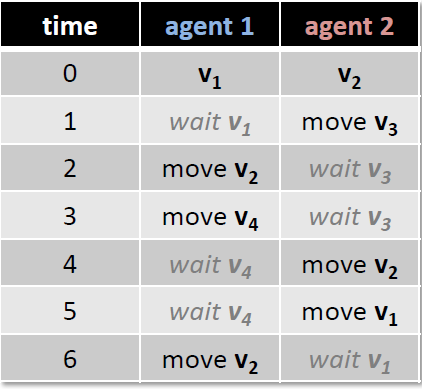
- if any agent is delayed then trains may cause collision during execution
- to prevent such collisions we may introduce more space between agents
K-robustness
- An agent can visit a node, if that node has not been occupied in recent k steps.
- 1-robustness covers both no-swap and no-train constraints (1번밖에 못 거치는것)
Other constraints
- No Plan(path) has a cycle
- No Two plans(paths) visit the same location
- waiting is not allowed
- some specific locations must be visited
How to Measure Quality of plans?
There are two typical criteria(to minimize):
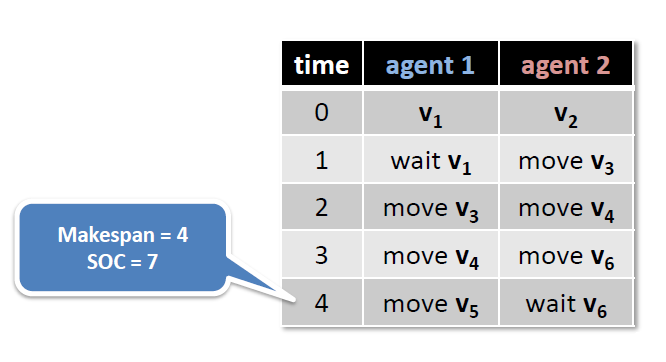
- Makespan
- distance between the start time of the first agent and the complete time of the last agent(아무개 에이전트의 시작과 아무개 에이전트의 마지막 동작)
- maximum of lengths of plans(end times)
- Sum of costs(SOC)
- Sum of lengths of plans(end times)
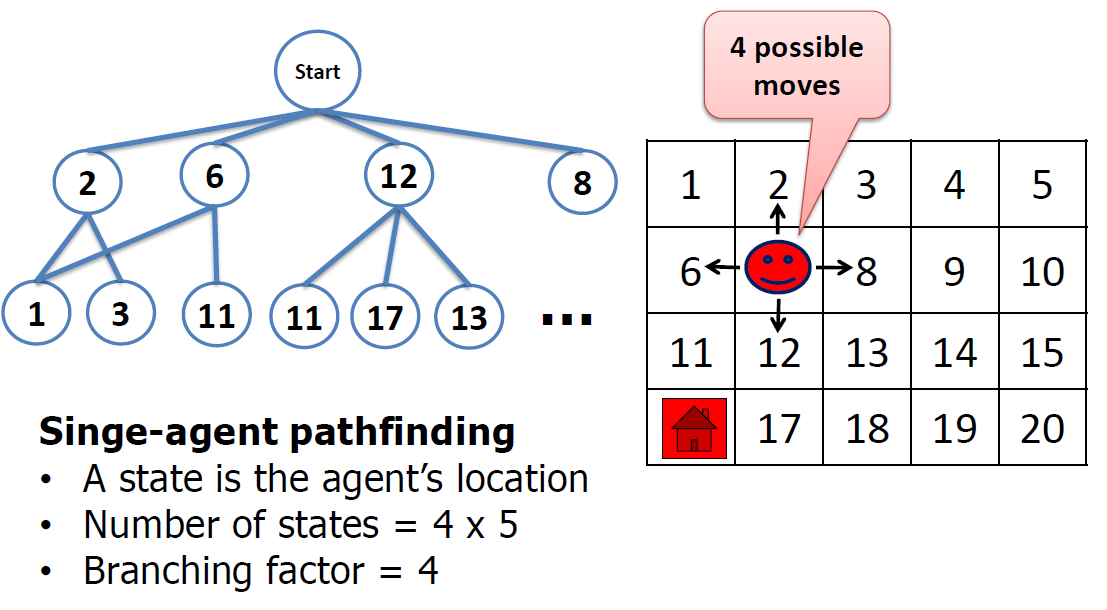
- Optimal single agent path finding is tractable(易处理的)
- e.g. Dijkstra’s algorithm
- Sub-optimal Multi-Agent path finding(with two free unoccupied nodes) is tractable
- e.g algorithm Push and Rotate
- MARF, where agents have joint goal nodes(it does not matter which agent reaches which goal) is tractable
- reduction to min-cost flow problem
- Optimal(Makespan,SOC) multi-agent path finding is NP-HARD
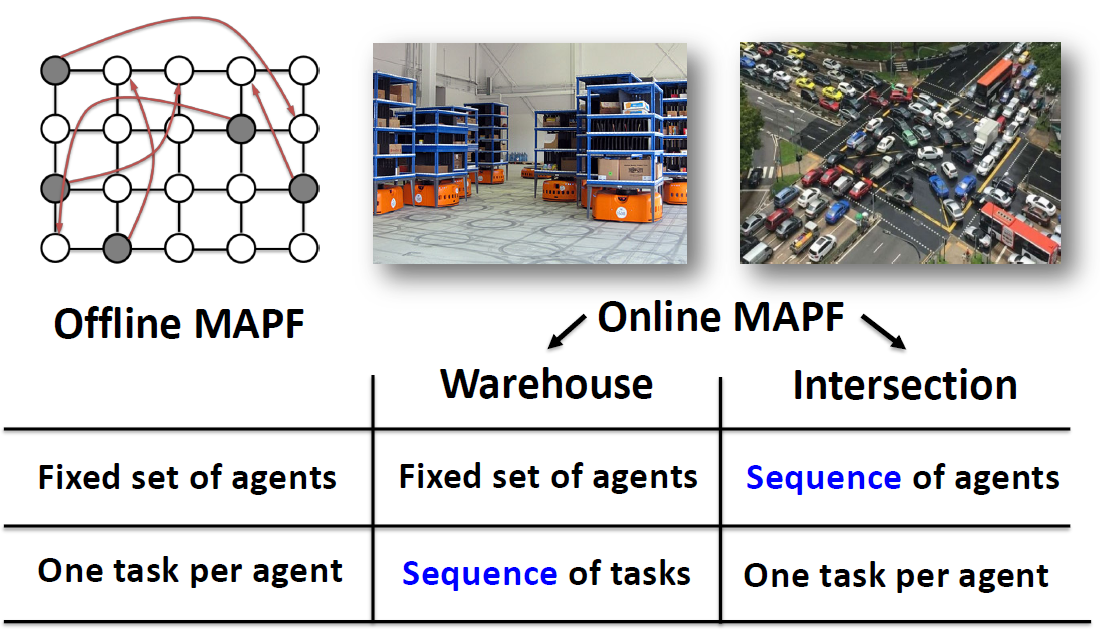
Solving approaches
- Search-Based Techniques
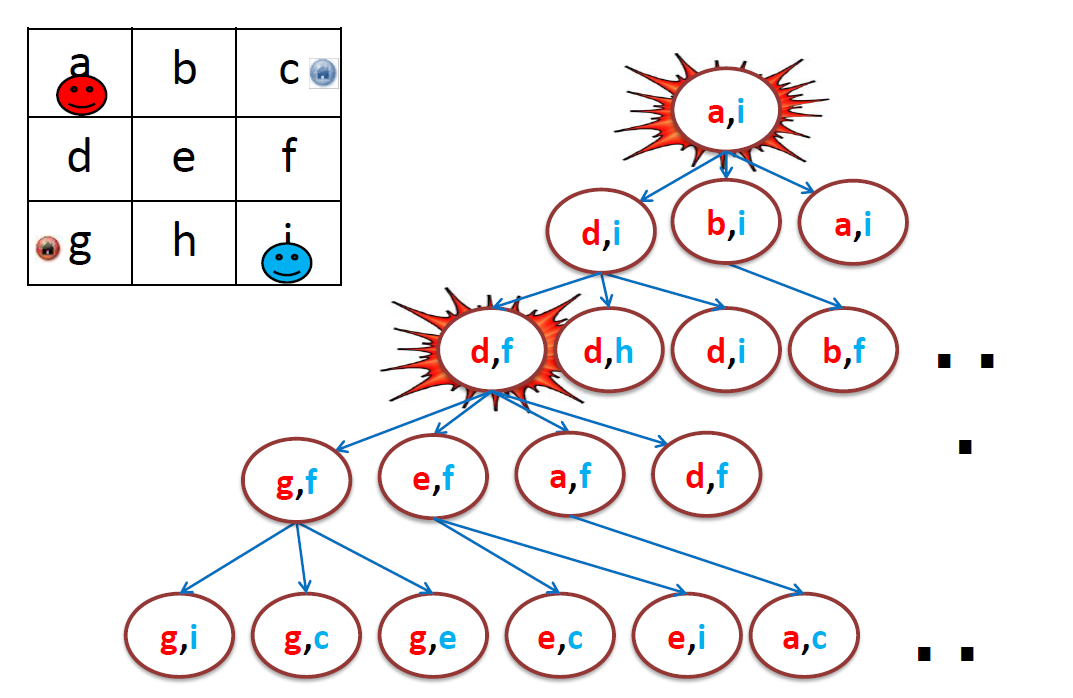
- state-space search(A*)
- state = location of agents at nodes
- transition = performing one action for each agent
- Conflict-based search
- ** Reduction-based Techniques
- Translate the problem to another formalism(形式主义)
- SAT/CSP/ASP …
2. Search-Based Solvers
- Search is a General Problem solving technique
- To expand or not expand, this is the question
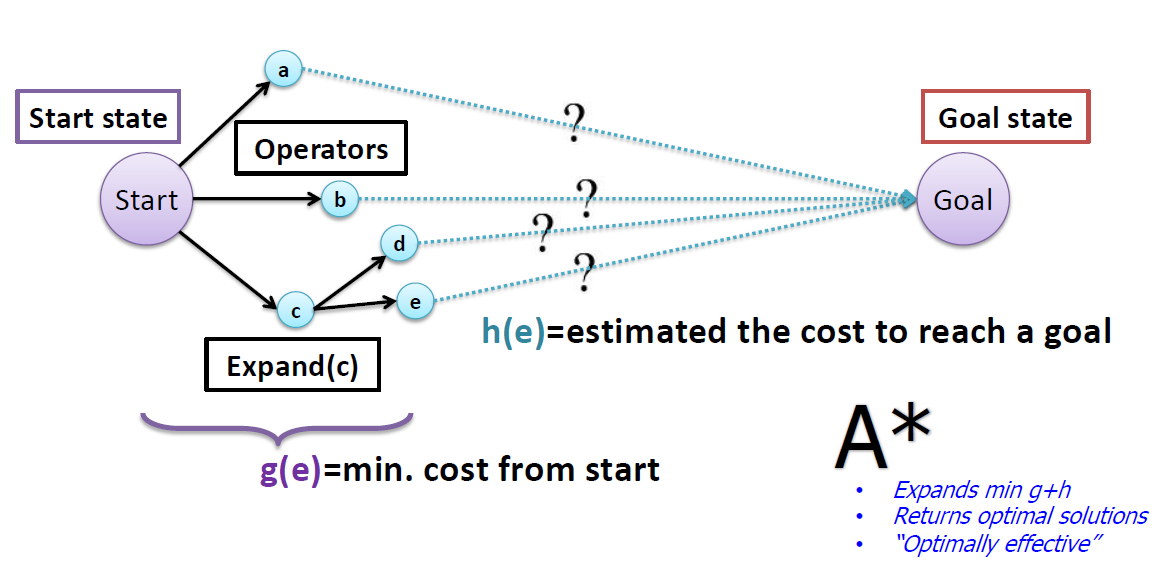
- Why do we need SEARCH for MAPF? Because it is Finding an optimal solution to hundreds of agents
- this is classical application of Search

- Solving Multi-Agent Path Finding with Search
- From A* to prioritized planners
- From prioritized(按重要性排列) planners back to A*
- The Increasing Cost tree search(ICTS)
- The Conflict-Based Search(CBS) framework
- Approximately optimal search-based solvers
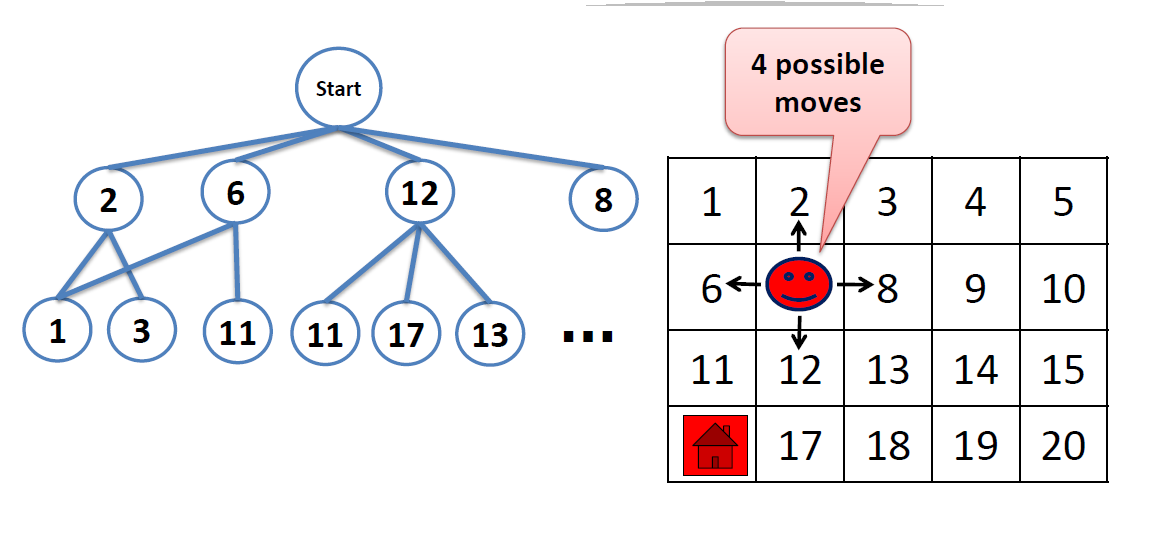
- Single Agent Search Problem Properties
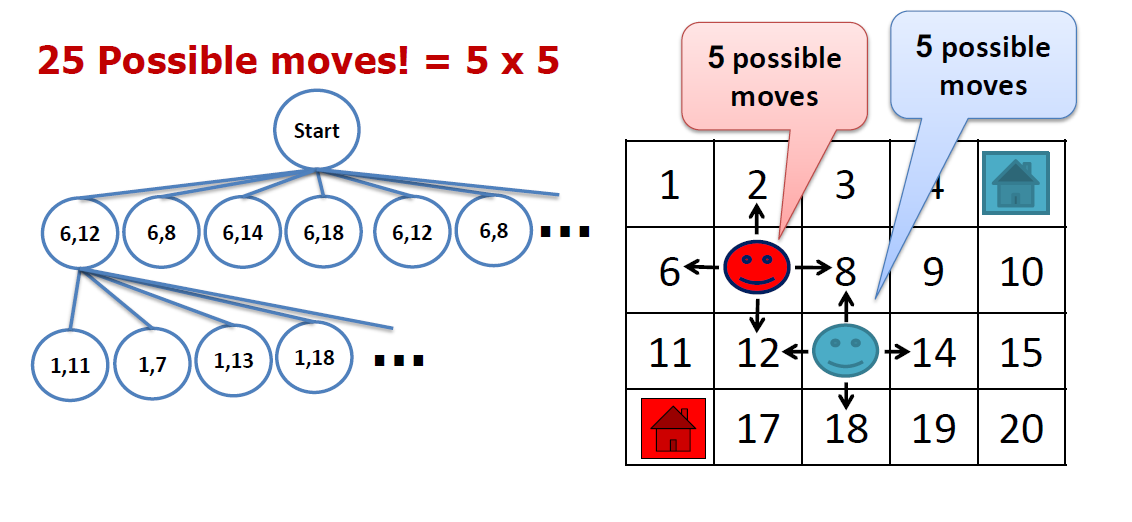
- Two Agent Search Problem Properties
- Number of States = ? ($20^2$)
- Branching factor = ? ($5^2$)
- then, What about K Agents?
- Number of States = ($20^k$)
- Branching factor = ($5^k$)
- IT IS VERY HARD PROBLEM
- SO Key Idea: Plan for each agent seperately
- Challenge: Maintaining soundness, completeness, and optimality
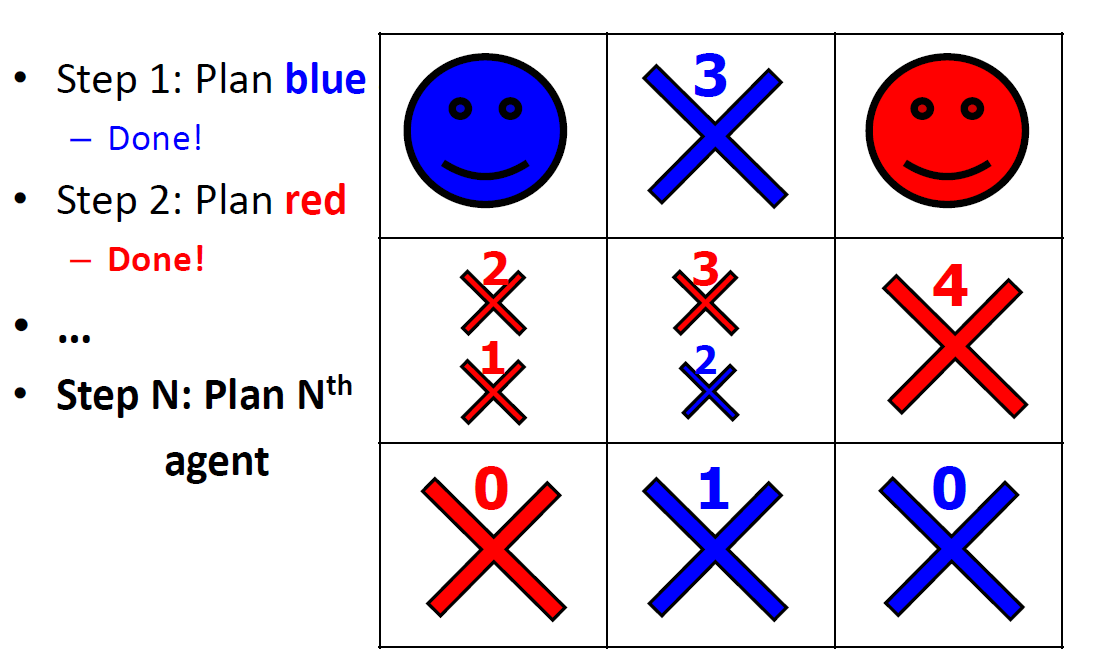
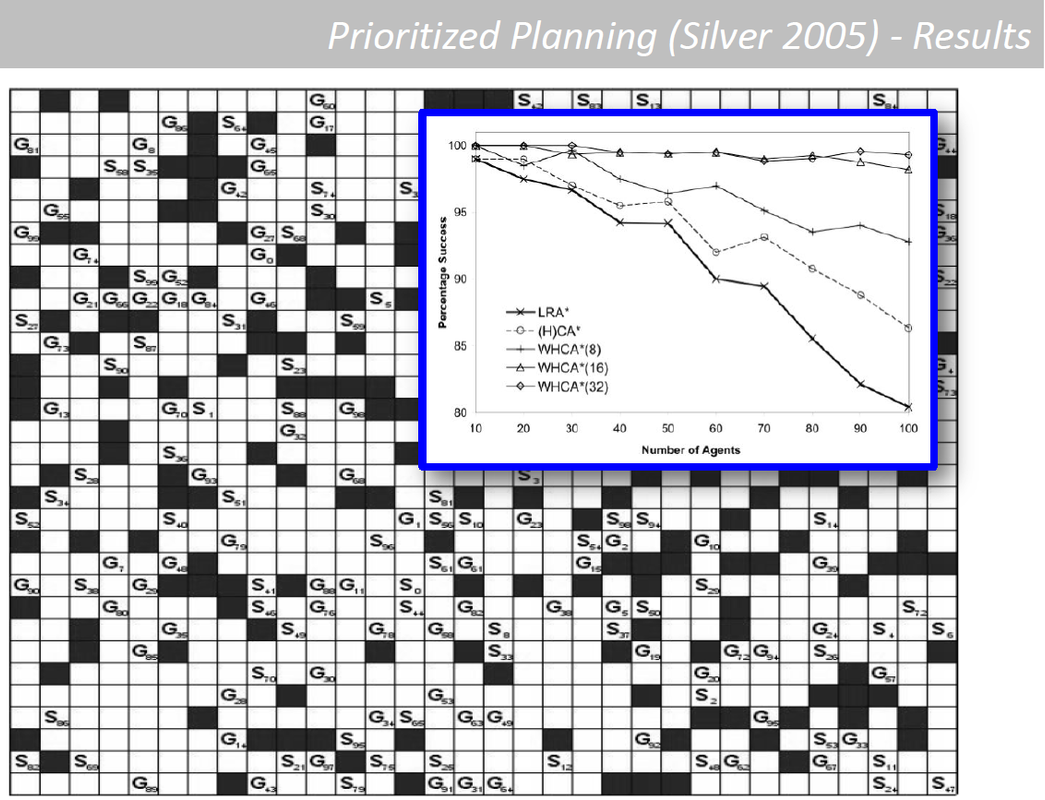
Prioritized Planning (Silver 2005) Analysis: First Agent
Prioritized Planning (Silver 2005) Analysis: Second Agent
- Complexity?
- Polynomial in the grid size and max time
- Soundness?
- Yes
- Complete? Optimal?
- No
- Smart Agent Prioritization
- conflict oriented WHCA*[Bnaya and Felner ‘14]
- Re-prioritization and safe intervals [Andreychuk and Yakovlev ‘18]
- Integrate planning and execution
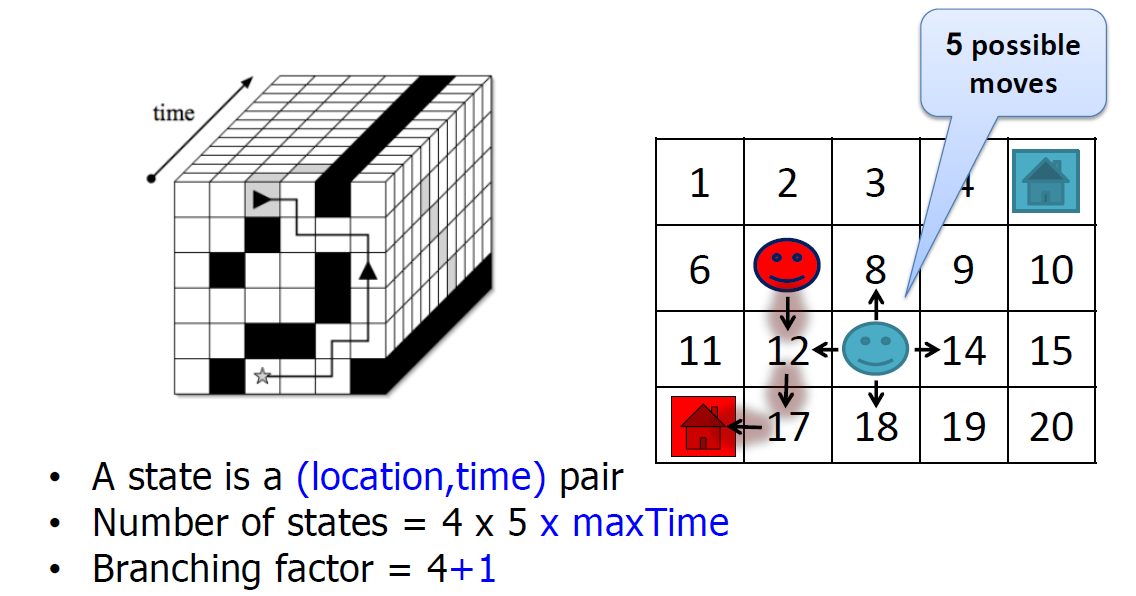
- High-level idea : reservation-based planning (ex) Number of states = 4 x 5 x maxTime)
- FAST, requires almost no coordination
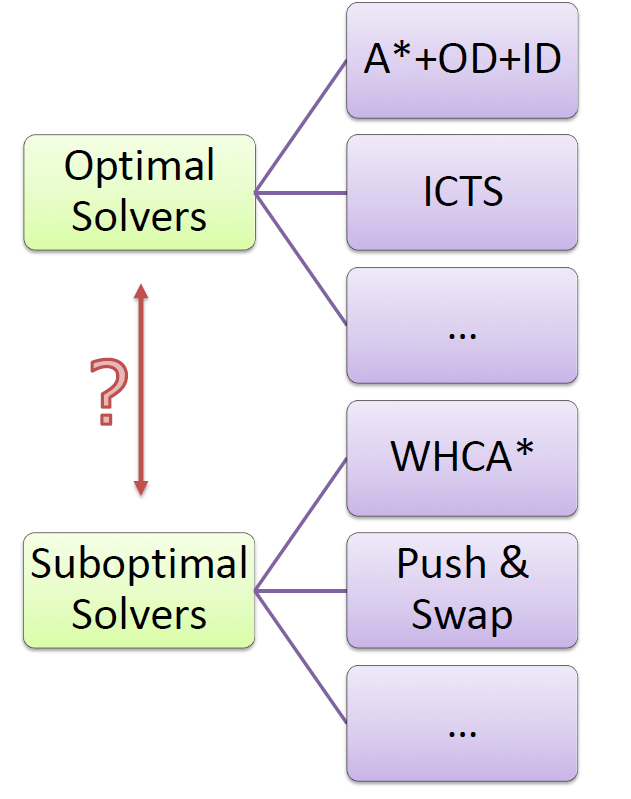
- Can MARF algorithm be Complete and efficient?
MAPF as a puzzle
- MAPF is highly related to pebble motion problems
- Each agent is a pebble(조약돌)
- Need to move each pebble to its goal
- cannot put two pebbles in one hole
- Pebble Motion can be solved Polynomial
- but far from optimally
- complex formulation
- Similar approaches
- slidable(滑动) Multi-Agent Path Planning[Wang & Botea, IJCAI, 2009]
- Push and Swap [Luna & Bekris, IJCAI, 2011]
- Parallel push and swap [Sajid, Luna, and Bekris, SoCS 2012]
- Push and Rotate [de Wilde et al. AAMAS 2013]
- Tree-based agent swapping strategy [Khorshid at el. SOCS, 2011]
Examples
Search based solver Summary
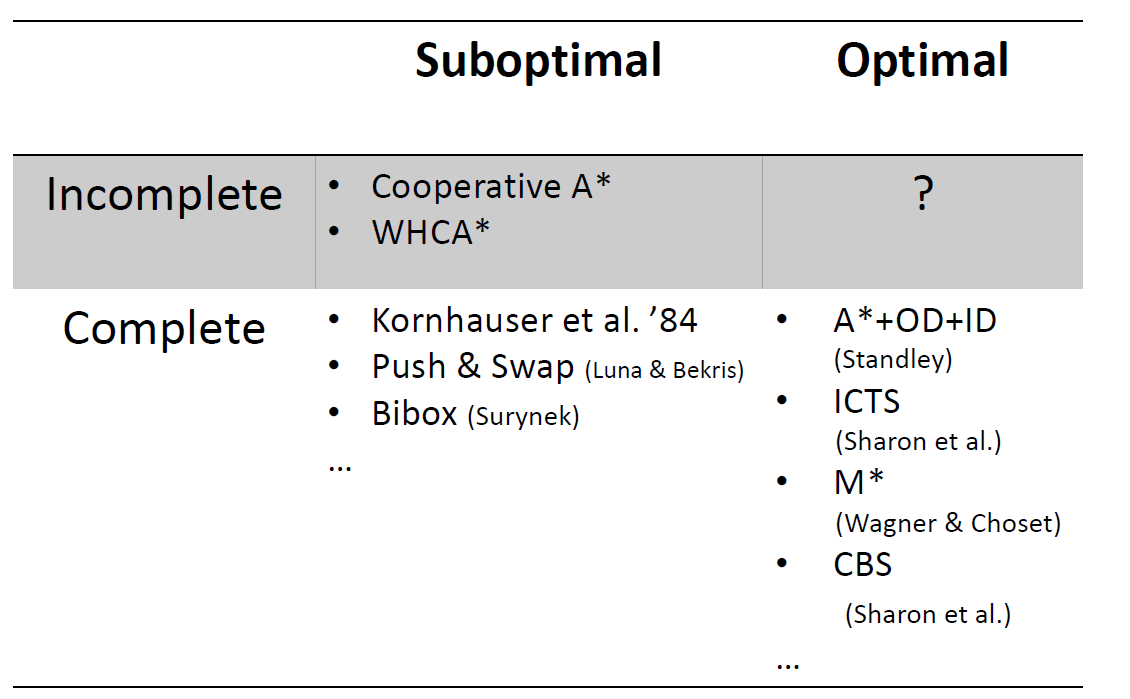
Can a MAPF algorithm be complete and efficient and optimal?
 On the Complexity of Optimal Parallel Cooperative Path-Finding, Surynek 2015
Planning Optimal Paths for Multiple Robots on Graphs, Yu and LaValle, 2013
On the Complexity of Optimal Parallel Cooperative Path-Finding, Surynek 2015
Planning Optimal Paths for Multiple Robots on Graphs, Yu and LaValle, 2013
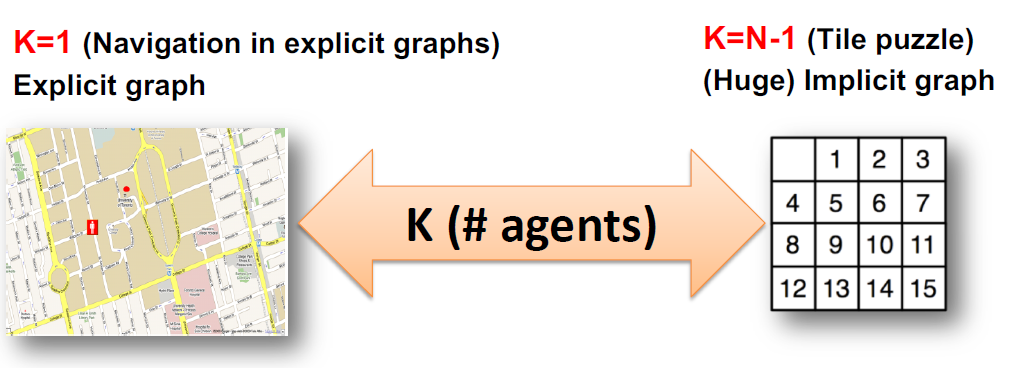
From Tiles to Agents
- Can we adpat technique from these extreme cases? answer is YES(invent some new techniques also(optimal MAPF))
- Searching the k-agent search space
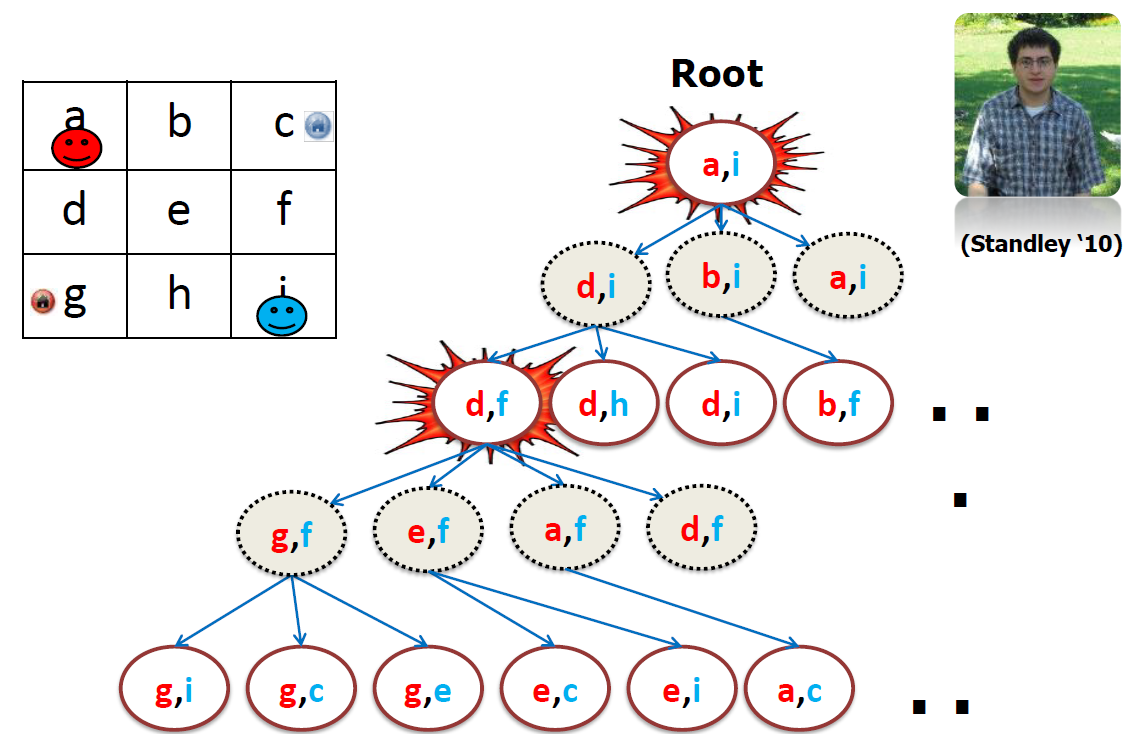
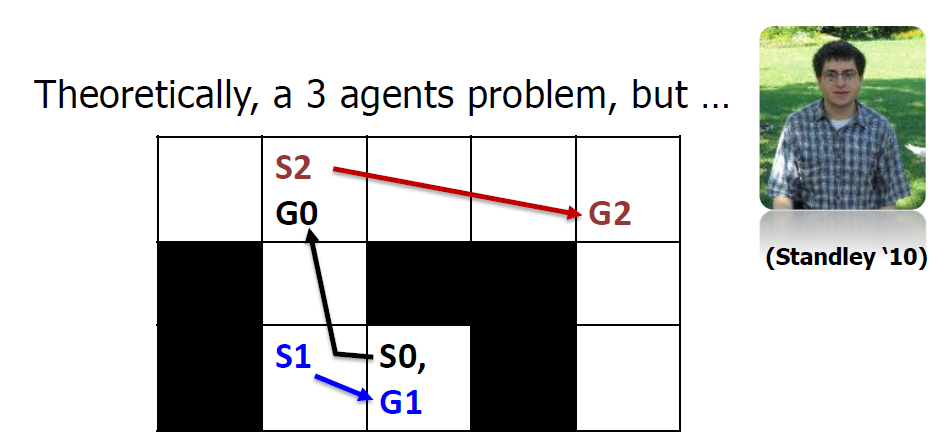
- A*+OD+ID [Standley ‘10]
- EPEA* [Felner ‘X, Goldenberg ‘Y]
- M* [Wagner & Choset ‘Z]
- Other search-based approaches
- ICTS [Sharon et al ‘13]
- CBS [Sharon et al ’15]
Optimal MARF with A*
- A* expands nodes
- A* gain efficiency by choosing which node to expand
What is the complexity of expanding a single node in MARF with 20 agents?
$5^20$ = 95,367,431,640,625
Search Tree Growth with Operator Decomposition
- Pros
- Branching factor is reduced to 5(= single agent)
- with a perfect heuristic can solve the problem
- Cons
- Solution is deeper by a factor of k
- More nodes may be expanded, due to intermediates
Enhanced Partial Expansion A*
Independence Detection
- Simple Independence Detection
- Independence Detection
- Solve optimally each agent separately
- While some agents conflict
-
- Try to avoid conflict, with the same cost
-
- Merge conflicting agents to one group
-
- Solve optimally new group
- but what if we have an environment like that
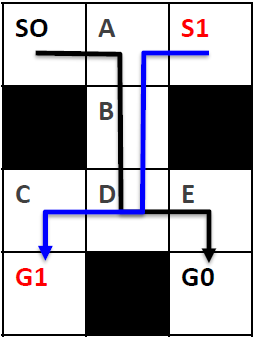
M* (Wagner & Choset ‘11,’14)
- Find optimal path for each agent individually

- Start the search. Generate only nodes on optimal paths

- If conflict occurs – backtrack and consider all ignored actions
Recursive M* (Wagner & Choset ‘11,’14)
- Recursive M*
- Find optimal path for each agent individually
- Start the search. Generate only nodes on optimal paths
- If conflict occurs – backtrack and consider all ignored actions
- Apply M* recursively after backtracking
- but problem is :
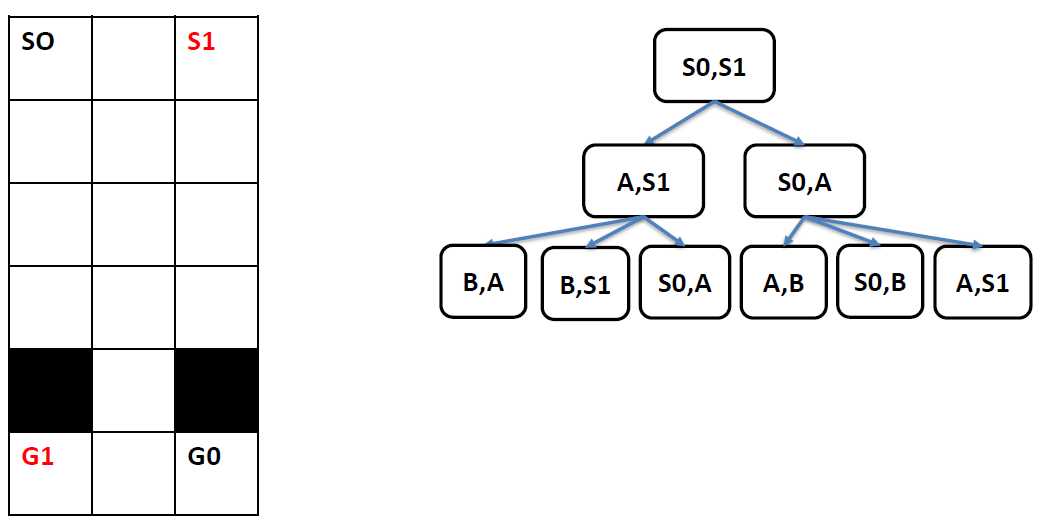
- joint path up to bottleneck can be long
Other Search-based approaches(ICTS,CBS)
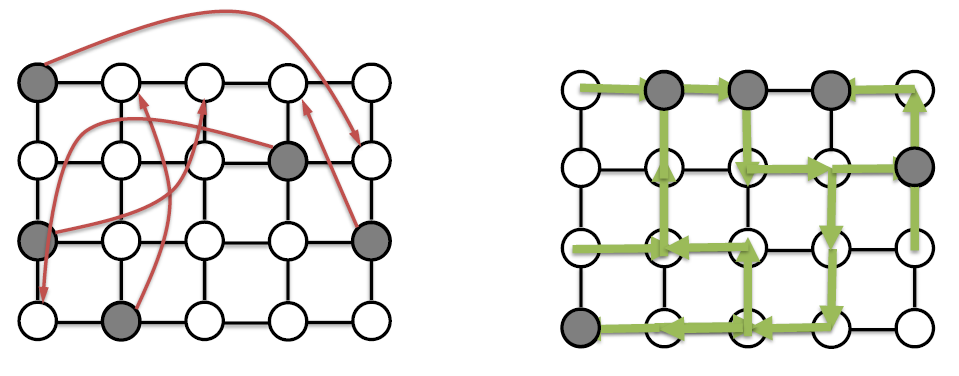
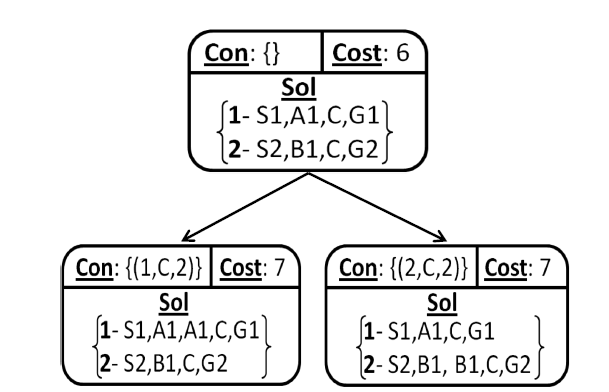
- Increasing Cost Tree Search (Sharon et al. ‘12)

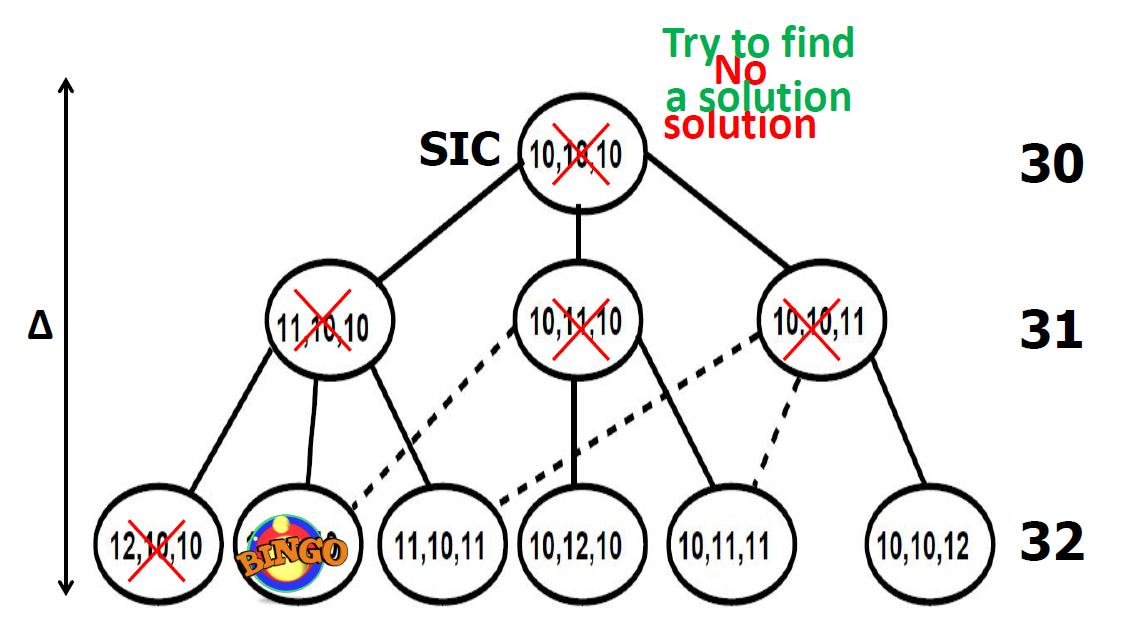

- Conflict Based Search(CBS)
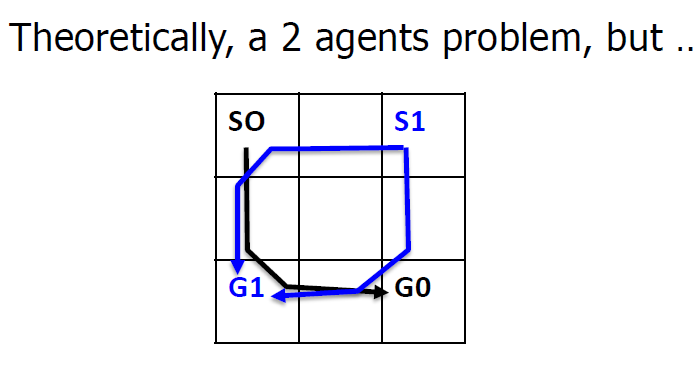
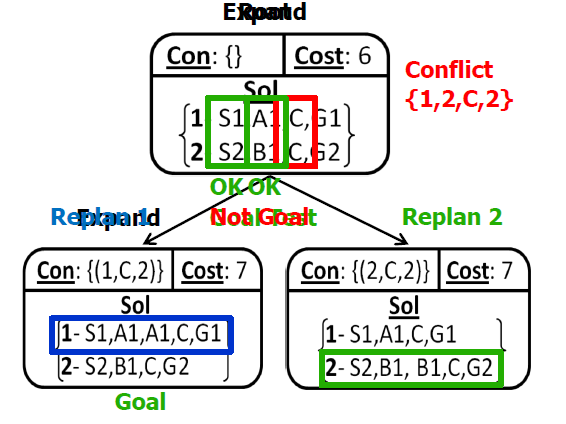
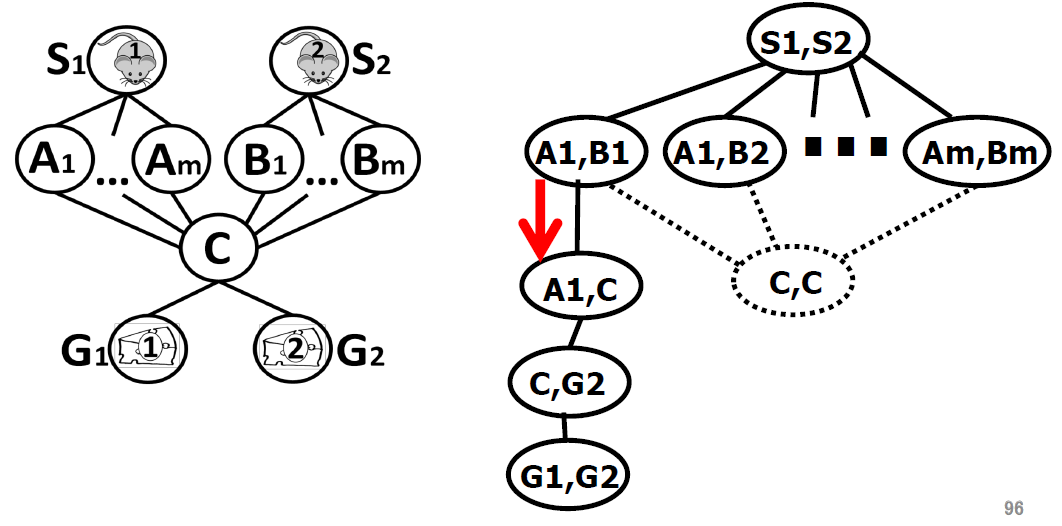
- Analysis: *Example 1**
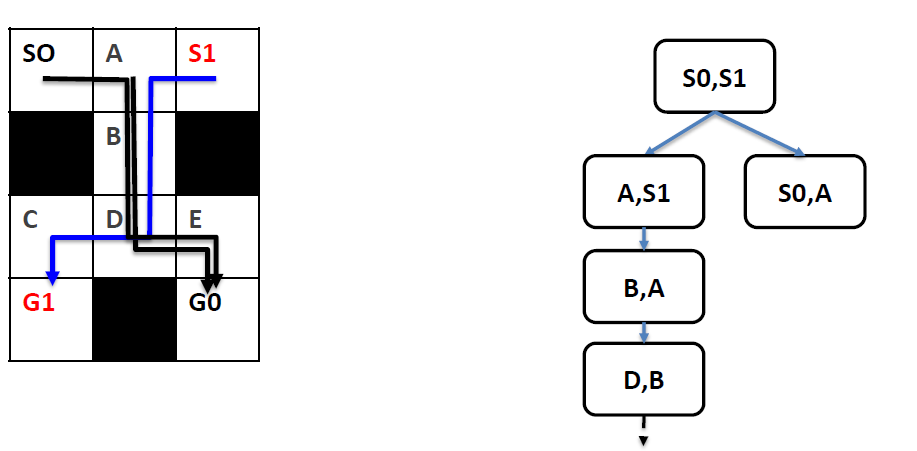
- Analysis: *Example 2**
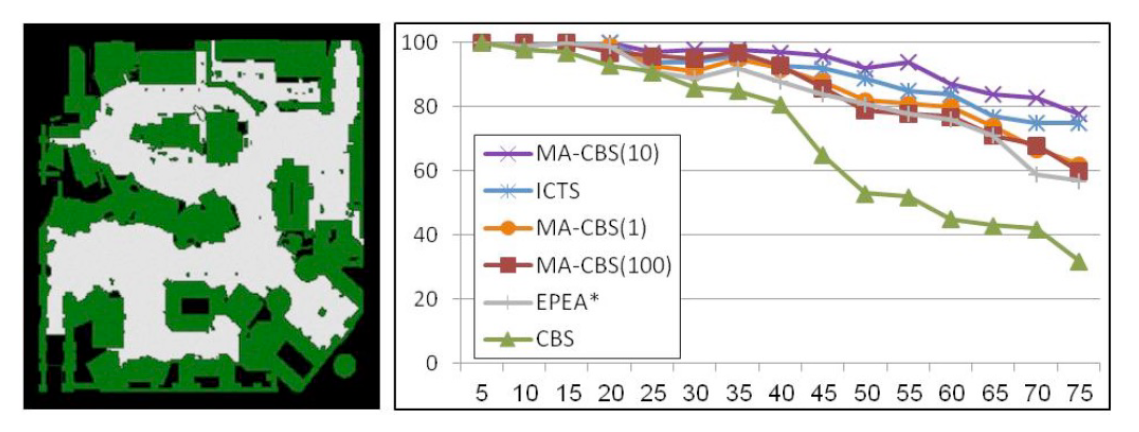
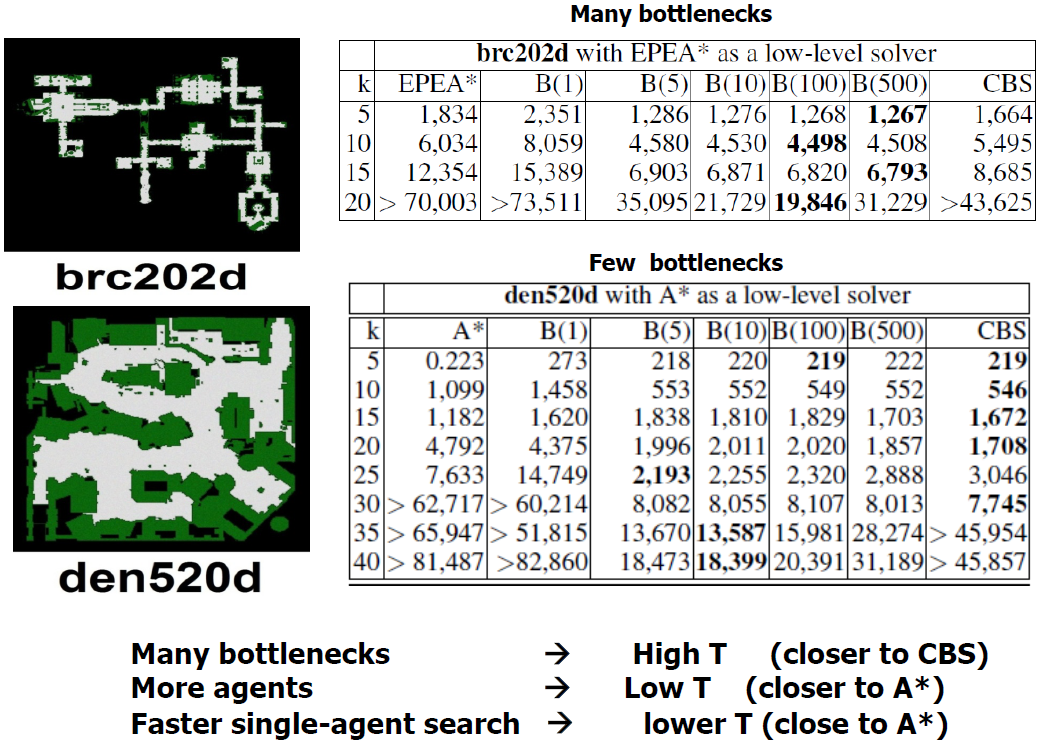
- Trends observed
- In open spaces: use A*
- In bottlenecks: use CBS
- What if we have both?
Meta-Agent CBS (MA-CBS)
- Plan for each agent individually
- Validate(确证) plans
- If the plans of agents A and B conflict
If (should merge(A,B))
merge A and B into a meta-agent
and solve with A*
Else
- Constrain A to avoid the conflicts or Constrain B to avoid the conflict
- Should Merge(A,B) (simple rule):
CBS Enhancements
- Which conflict to resolve? [Boyarski et al. ‘16]
- What to do after merging? [Boyarski et al. ‘16]
- Heuristics for the constraint tree search [Felner et al. ‘18]
- Augmenting CBS with human knowledge [Cohen et al.]
- Which low-level solver to use?
- When to merge the agents ?
Summary
- A* (M, EPEA, A*+OD+ID)
- Main factors: #agents, graph size, heuristic accuracy
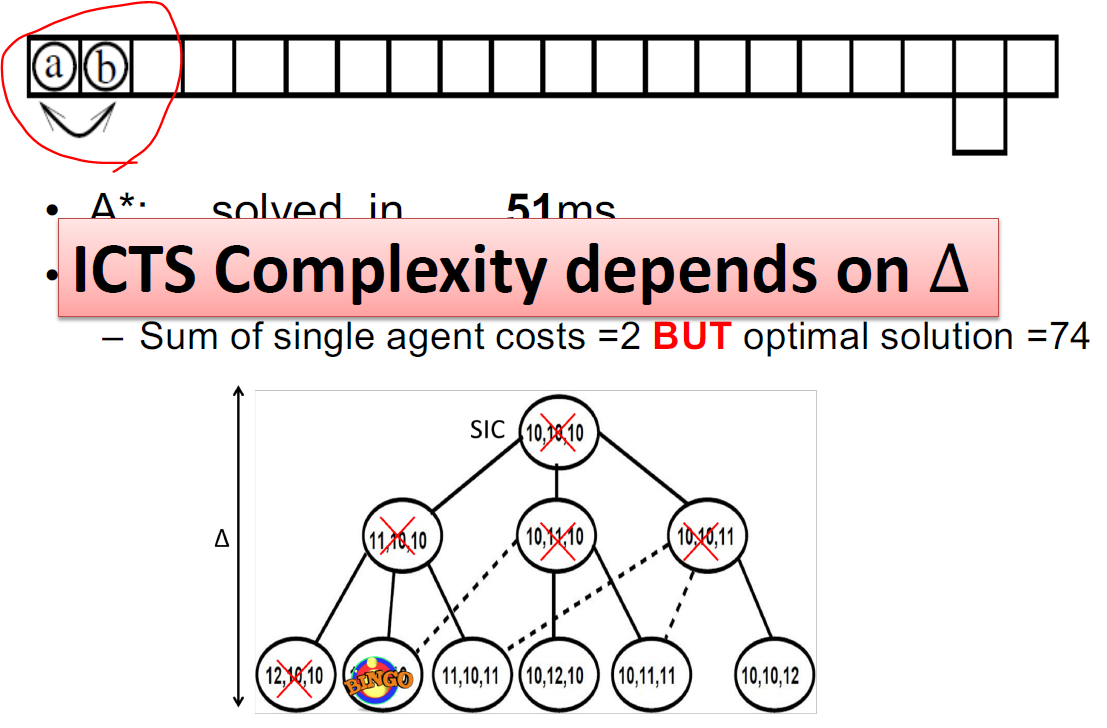
- ICTS
- Main factors: #agents, Δ, graph size
- CBS and its variants
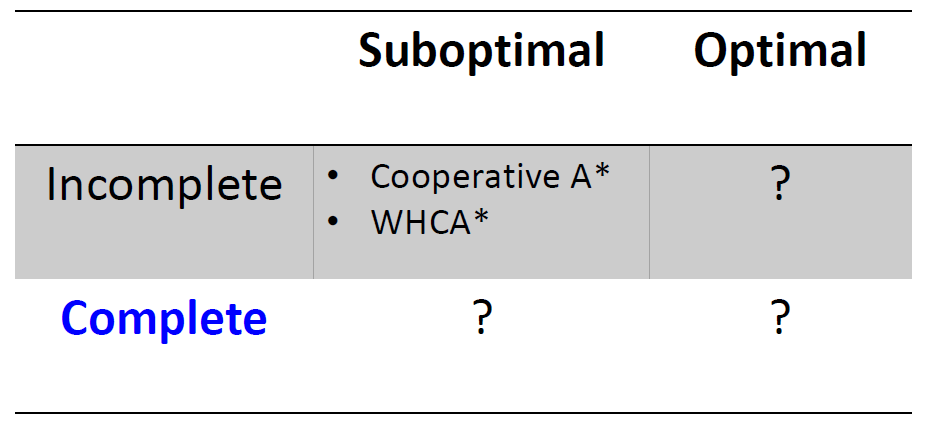
Solving MAPF
Bounded Suboptimal Algorithms
- An algorithm is bounded suboptimal iff
- It accepts a parameter !
- It outputs a solution whose cost is at most 1 + ! ⋅Optimal
- How to create a bounded suboptimal algorithm?
- Different search algorithms
- Inadmissible(不允许的) heuristics
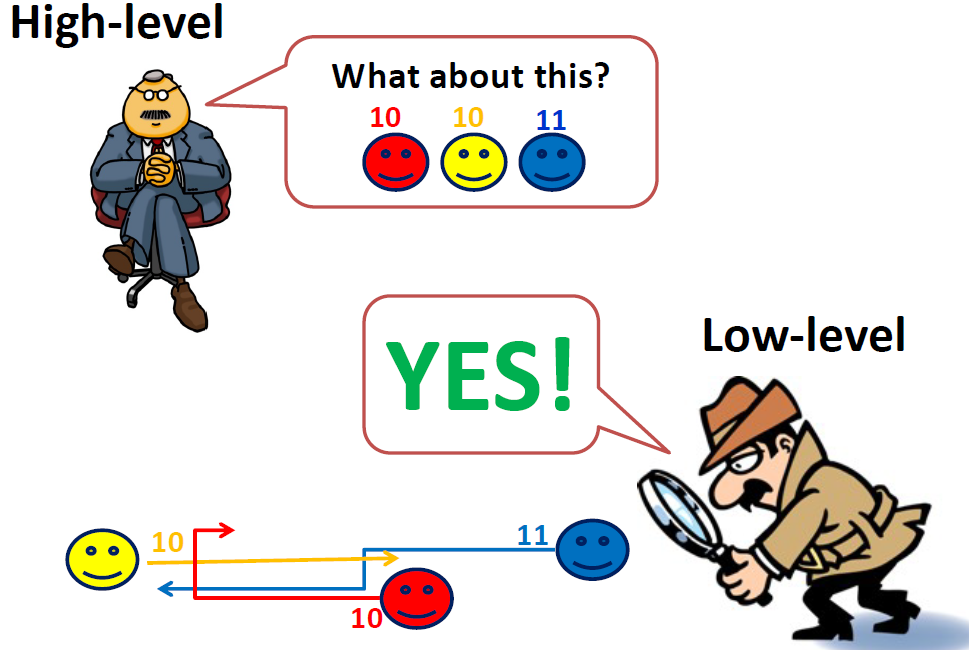
Suboptimal ICTS
Suboptimal A*
Suboptimal M*
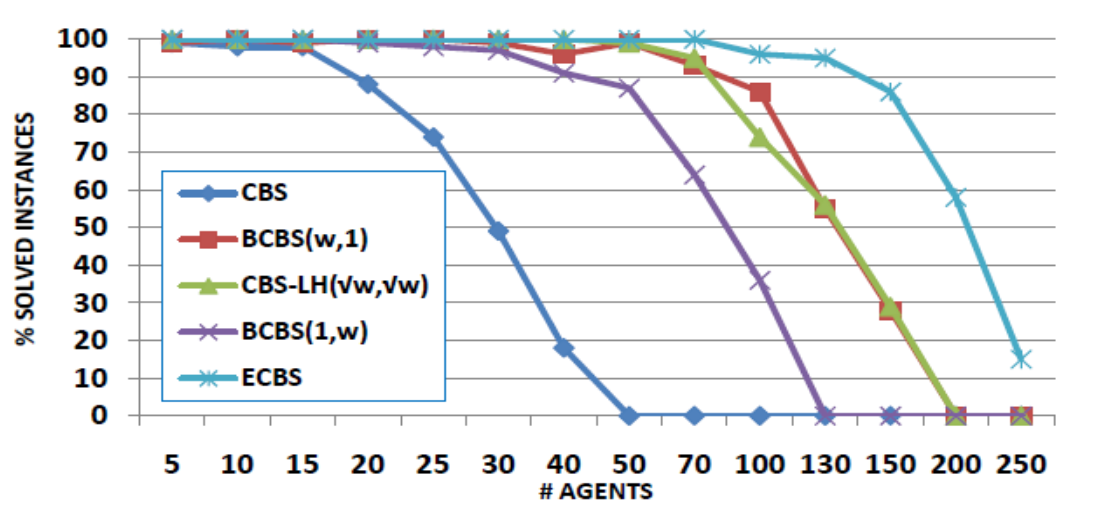
Suboptimal CBS
- Observation: Suboptimality can be introduced in both levels
Advanced Issues in Search-based MAPF Algorithms
- When to use which algorithm? Ensembles(全体)?
- Using knowledge about past plans (Cohen et al. ’15)
- Stronger heuristics for all algorithms
- Deeper analysis of algorithms’ complexity
- Beyond grid worlds
- Kinematic constraints (Ma et al. ‘16)
- Any-angle planning (Yakovlev et al. ‘17)
- Hierarchical environments (Walker et al. ’17)
- Large agents (Li et al. ‘19)
- Priorized planning based on CBS (Ma et al. ‘19)
- Planning & execution
Reference: postassco
Multi-Agent path finding(MAPF)
- Multi-Agent(many robot) play to find the target position and move
- MAPF problem: Find a collision-free plan(path) for each agent
- Another name we called it : Cooperative path finding(CPF), Multi-robot path planning, pebble(鹅卵石) motion
1) Introduction to MAPF
- a graph (directed or undirected)
- a set of agents(robot), each agent is assigned to two locations(nodes) in the graph(start, destination)
- Each agent can perform either move(to a neighbouring node) or wait(in the same node) actions
Typical Assumption: all move and wait actions have identical durations(plans for agents are synchronized)
- Plan is a sequence of actions for the agent leading from its start location to its destination
- the length of plan(for an agent) is defined by the time when the agent reaches its destination and does not leave it anymore.
- Find Plans for all agents such that the plans do not collide in time and space (no two agents are at the same location at the same time)

- some necessary conditions for plan existence:
- no two agents are at the same start node
- no two agents share the same destination node(unless an agent disappears when reaching its destination)
- the number of agents is strictly smaller than the number of nodes
- agent at $v_i$ cannot perform move $v_j$ at the same time when agent at $v_j$ perform move $v_i$
- Agents may swap position. but agents use the same edges at the same time, swap is not allowed

- Agent can approach node that is currently occupied but will be free before arrival(Agent at $v_i$ cannot perform move $v_j$ if there is another agent at $v_j$)

- if any agent is delayed then trains may cause collision during execution
- to prevent such collisions we may introduce more space between agents
K-robustness
- An agent can visit a node, if that node has not been occupied in recent k steps.
- 1-robustness covers both no-swap and no-train constraints (1번밖에 못 거치는것)
Other constraints
- No Plan(path) has a cycle
- No Two plans(paths) visit the same location
- waiting is not allowed
- some specific locations must be visited
How to Measure Quality of plans?
There are two typical criteria(to minimize):

- Makespan
- distance between the start time of the first agent and the complete time of the last agent(아무개 에이전트의 시작과 아무개 에이전트의 마지막 동작)
- maximum of lengths of plans(end times)
- Sum of costs(SOC)
- Sum of lengths of plans(end times)
- Optimal single agent path finding is tractable(易处理的)
- e.g. Dijkstra’s algorithm
- Sub-optimal Multi-Agent path finding(with two free unoccupied nodes) is tractable
- e.g algorithm Push and Rotate
- MARF, where agents have joint goal nodes(it does not matter which agent reaches which goal) is tractable
- reduction to min-cost flow problem
- Optimal(Makespan,SOC) multi-agent path finding is NP-HARD

Solving approaches
- Search-Based Techniques
- state-space search(A*)
- state = location of agents at nodes
- transition = performing one action for each agent
- Conflict-based search
- state-space search(A*)
- ** Reduction-based Techniques
- Translate the problem to another formalism(形式主义)
- SAT/CSP/ASP …
- Translate the problem to another formalism(形式主义)
2. Search-Based Solvers
- Search is a General Problem solving technique
- To expand or not expand, this is the question

- Why do we need SEARCH for MAPF? Because it is Finding an optimal solution to hundreds of agents
- this is classical application of Search

- Solving Multi-Agent Path Finding with Search

- From A* to prioritized planners
- From prioritized(按重要性排列) planners back to A*
- The Increasing Cost tree search(ICTS)
- The Conflict-Based Search(CBS) framework
- Approximately optimal search-based solvers

- Single Agent Search Problem Properties
- Two Agent Search Problem Properties
- Number of States = ? ($20^2$)
- Branching factor = ? ($5^2$)
- then, What about K Agents?
- Number of States = ($20^k$)
- Branching factor = ($5^k$)
- IT IS VERY HARD PROBLEM
- SO Key Idea: Plan for each agent seperately
- Challenge: Maintaining soundness, completeness, and optimality

Prioritized Planning (Silver 2005) Analysis: First Agent
Prioritized Planning (Silver 2005) Analysis: Second Agent
- Complexity?
- Polynomial in the grid size and max time
- Soundness?
- Yes
- Complete? Optimal?
- No
- Smart Agent Prioritization
- conflict oriented WHCA*[Bnaya and Felner ‘14]
- Re-prioritization and safe intervals [Andreychuk and Yakovlev ‘18]
- Integrate planning and execution
- High-level idea : reservation-based planning (ex) Number of states = 4 x 5 x maxTime)
- FAST, requires almost no coordination
- Can MARF algorithm be Complete and efficient?
MAPF as a puzzle
- MAPF is highly related to pebble motion problems
- Each agent is a pebble(조약돌)
- Need to move each pebble to its goal
- cannot put two pebbles in one hole
- Pebble Motion can be solved Polynomial
- but far from optimally
- complex formulation
- Similar approaches
- slidable(滑动) Multi-Agent Path Planning[Wang & Botea, IJCAI, 2009]
- Push and Swap [Luna & Bekris, IJCAI, 2011]
- Parallel push and swap [Sajid, Luna, and Bekris, SoCS 2012]
- Push and Rotate [de Wilde et al. AAMAS 2013]
- Tree-based agent swapping strategy [Khorshid at el. SOCS, 2011]
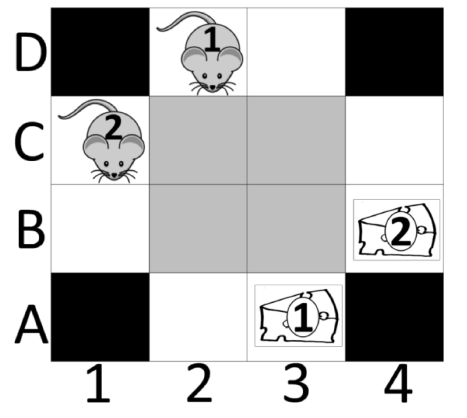
Examples
Search based solver Summary
Can a MAPF algorithm be complete and efficient and optimal?
 On the Complexity of Optimal Parallel Cooperative Path-Finding, Surynek 2015
Planning Optimal Paths for Multiple Robots on Graphs, Yu and LaValle, 2013
On the Complexity of Optimal Parallel Cooperative Path-Finding, Surynek 2015
Planning Optimal Paths for Multiple Robots on Graphs, Yu and LaValle, 2013
From Tiles to Agents
- Can we adpat technique from these extreme cases? answer is YES(invent some new techniques also(optimal MAPF))

- Searching the k-agent search space
- A*+OD+ID [Standley ‘10]
- EPEA* [Felner ‘X, Goldenberg ‘Y]
- M* [Wagner & Choset ‘Z]
- Other search-based approaches
- ICTS [Sharon et al ‘13]
- CBS [Sharon et al ’15]
Optimal MARF with A*
- A* expands nodes
- A* gain efficiency by choosing which node to expand
What is the complexity of expanding a single node in MARF with 20 agents?
$5^20$ = 95,367,431,640,625
Search Tree Growth with Operator Decomposition
- Pros
- Branching factor is reduced to 5(= single agent)
- with a perfect heuristic can solve the problem
- Cons
- Solution is deeper by a factor of k
- More nodes may be expanded, due to intermediates
Enhanced Partial Expansion A*
Independence Detection
- Simple Independence Detection
- Independence Detection
- Solve optimally each agent separately
- While some agents conflict
-
- Try to avoid conflict, with the same cost
-
- Merge conflicting agents to one group
-
- Solve optimally new group
-
- but what if we have an environment like that

M* (Wagner & Choset ‘11,’14)
- Find optimal path for each agent individually

- Start the search. Generate only nodes on optimal paths

- If conflict occurs – backtrack and consider all ignored actions
Recursive M* (Wagner & Choset ‘11,’14)
- Recursive M*
- Find optimal path for each agent individually
- Start the search. Generate only nodes on optimal paths
- If conflict occurs – backtrack and consider all ignored actions
- Apply M* recursively after backtracking
- but problem is :

- joint path up to bottleneck can be long
Other Search-based approaches(ICTS,CBS)
- Increasing Cost Tree Search (Sharon et al. ‘12)




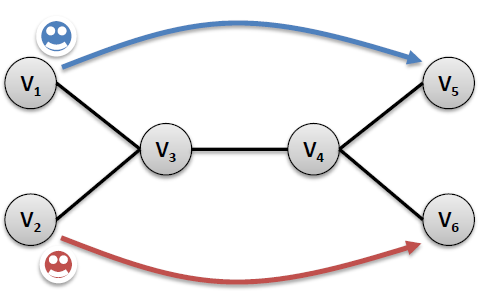
- Conflict Based Search(CBS)
- Analysis: *Example 1**
- Analysis: *Example 2**
- Trends observed
- In open spaces: use A*
- In bottlenecks: use CBS
- What if we have both?
Meta-Agent CBS (MA-CBS)
- Plan for each agent individually
- Validate(确证) plans
- If the plans of agents A and B conflict
If (should merge(A,B)) merge A and B into a meta-agent and solve with A* Else - Constrain A to avoid the conflicts or Constrain B to avoid the conflict
- Should Merge(A,B) (simple rule):
CBS Enhancements
- Which conflict to resolve? [Boyarski et al. ‘16]
- What to do after merging? [Boyarski et al. ‘16]
- Heuristics for the constraint tree search [Felner et al. ‘18]
- Augmenting CBS with human knowledge [Cohen et al.]
- Which low-level solver to use?
- When to merge the agents ?
Summary
- A* (M, EPEA, A*+OD+ID)
- Main factors: #agents, graph size, heuristic accuracy
- ICTS
- Main factors: #agents, Δ, graph size
- CBS and its variants
Solving MAPF
Bounded Suboptimal Algorithms
- An algorithm is bounded suboptimal iff
- It accepts a parameter !
- It outputs a solution whose cost is at most 1 + ! ⋅Optimal
- How to create a bounded suboptimal algorithm?
- Different search algorithms
- Inadmissible(不允许的) heuristics
Suboptimal ICTS
Suboptimal A*
Suboptimal M*
Suboptimal CBS
- Observation: Suboptimality can be introduced in both levels
Advanced Issues in Search-based MAPF Algorithms
- When to use which algorithm? Ensembles(全体)?
- Using knowledge about past plans (Cohen et al. ’15)
- Stronger heuristics for all algorithms
- Deeper analysis of algorithms’ complexity
- Beyond grid worlds
- Kinematic constraints (Ma et al. ‘16)
- Any-angle planning (Yakovlev et al. ‘17)
- Hierarchical environments (Walker et al. ’17)
- Large agents (Li et al. ‘19)
- Priorized planning based on CBS (Ma et al. ‘19)
- Planning & execution
Reference: postassco











Comments