Multi-Agent path finding(MAPF) & REDUCTION-BASED SOLVERS
27 Sep 2019 | ROBOTICS
REDUCTION-BASED SOLVERS
- How to exploit knowledge of others for solving own problems?
- by translating the problem P to another problem Q (문제를 바꾼다)
- Why is it useful?
- If anybody improves the solver for Q then we get an improved solver for P for free
- Staying on the shoulders of giants
- Reduction, compilation, re-formulation techniques
- Boolean satisfiability
- fast SAT solvers
- Constraint programming
- global constraints for pruning(修剪树枝) search space
- Answer set programming
- declarative(陈述的) framework
- Combinatorial auctions
- a Boolean satisfiability (SAT)
1. Introduction to SAT
- Express (model) the problem as a SAT formula in a conjunctive normal form (CNF)
- a Boolean satisfiability (SAT)
Boolean variables (true/false values)
clause = a disjunction(分离) of literals (variables and negated(使无效) variables)
formula = a conjunction of clauses
solution = an instantiation of variables such that the formula is satisfied
Example:
(X or Y ) and (not X or not Y)
[exactly one of X and Y is true]
- SAT model is expressed as a CNF formulaConjunctive normal form
- We can go beyond CNF and use abstract expressions that are translated to CNF
- We can even use numerical variables (and constraints).
2. SAT encoding: core idea
- In MAPF, we do not know the lengths of plans (due to possible re-visits of nodes)!
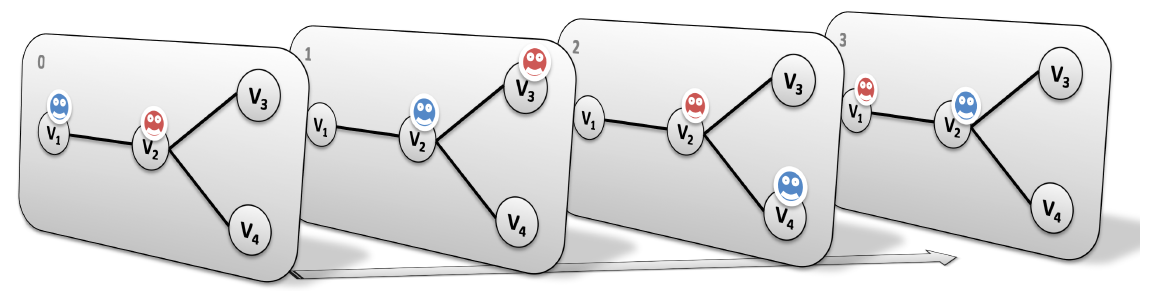
- We can encode(把…译成电码) plans of a known length using a layered graph (temporally extended graph).
- Each layer corresponds to one time slice and indicates positions of agents at that time
3. SAT encoding with all-different
- Uses multi-valued state variables (logarithmic encoding) encoding position of agents in layers (∧ = And, ∨ = OR)
- Agent waits or moves to a neighbor
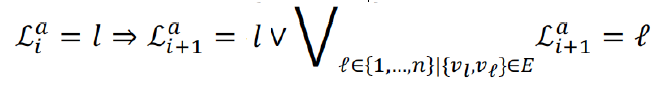
- No-train constraint
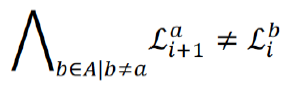
- Agents are not at the same nodes
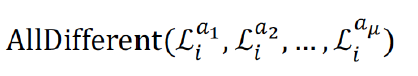
4. Direct SAT encoding
- Directly encodes positions of agents in layers
- Agent is placed at exactly one node in each layer (¬ 논리 부정)
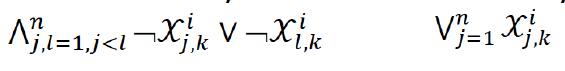
- No two agents are placed at the same node in each layer
- Agent waits or moves to a neighbor
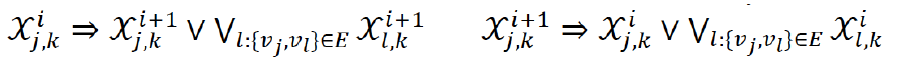
- No-swap and no-train (nodes before and after move are empty)
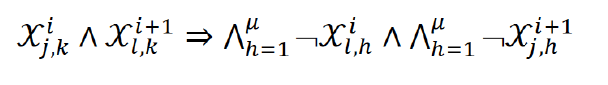
5. Comparison of SAT encodings
Finding makespan optimal solutions
(composition with Independence Detection (OD+ID))
6. Mixed model
- Using layered graph describing agent positions at each time step
- $B_tav$ : agent a occupies vertex(顶点) v at time t
- Constraints:
- each agent occupies exactly one vertex at each time
- no two agents occupy the same vertex at any time.
- if agent a occupies vertex v at time t, then a occupies a neighboring vertex or stay at v at time t + 1.
- Preprocessing:
- $B_tav$ = 0 if agent a cannot reach vertex v at time t or a cannot reach the destination being at v at time t
import sat
def path (N,As):
K = len(As)
lower_upper_bounds(As,LB,UB) # Incremental generation of layers
between(LB,UB,M),
B = new_array(M+1, K,N),
B :: 0..1,
% Initialize the first and last states(Setting the initial and destination locations)
foreach(循环) (A in 1..K)
(V,FV) = As[A]
B[1,A,V] = 1,
B[M+1,A,FV] = 1
end,
% Each agent occupies exactly one vertex
foreach(T in 1..M+1, A in 1..K)
sum([B[T,A,V]] : V in 1..N) #=1
end,
% No two agents occupy the same vertex (No Conflict between agents)
foreach ( T in 1..M+1, V in 1..K)
sum([B[T,A,V] : A in 1..K]) # =1
% Every Transition is valid(Agent moves to a neighboring vertex)
foreach (T in 1..M, A in 1..K, V in 1..N)
neibs(V,neibs),
B[T,A,V] # =>
sum([B[T+1, A, U]: U in neibs]) #>= 1
end,
% K-robustness
foreach(T in 1..M1, A in 1..K, V in 1..N)
B[T,A,V] # => sum([B[Prev,A2,V]:
A2 in 1..K, A2!=A
prev in max(1,T-L)..T]) # = 0
end,
solve(B)
output_plan(B)
- Picat provides assignment and loop statements for programming everyday things.
- a Boolean satisfiability (SAT)
- Assembly Sequence Planning (ASP)
7. Objectives in SAT
- Makespan (minimize the maximum end time)
- incrementally add layers until a solution found
- Sum of cost (minimize the sum of end times)
- incrementally add layers and look for the SOC optimal solution in each iteration (makespan + SOC optimal)
- generate more layers (upper bound) and then optimize SOC (naïve)
- incrementally add layers and increase the cost limit until a solution is found [Surynek et al, ECAI 2016]
8. Real World
- Objective
- How to develop robust and scalable AI technology for dealing with complex dynamic application scenarios?
- What’s needed?
- a model scenario
- Robotic intra-logistics (물류)
- why?
- rich : multi-faceted, full of variations
- scalable : layout, objects, granularity(粒度)
- measurable : makespan, energy, quality of service
- integrative(综合的) : mapf, data, constraints, decisions
- relevant : industry 4.0
- Robotics systems for logistics(物流) and warehouse automation based on many mobile robots and movable shelves
- Main tasks: order fulfillment(routing(路由), order picking, replenishment(补充))
- Many competing industry solutions : Amazon, Dematic, Genzebach, Gray Orange, Swisslog
- what’s in the environment?
- Objects : floor, robots, shelves, products, people, etc
- Relations : positions, carries/d, capacity, orientation, durations, etc
- Actions : move, pickup, putdown, pick, charge, restock, etc.
- Objectives : deadlines, throughput, exploitation, energy management, human machine interaction, etc.
9. Beyond MAPF
- Classified by objects, measurability, constraints, decisions
- MAPF (Multi-Agent Path Finding)
- Most simple, straightforwards extension of APF
- Objects: only robots and the map
- anonymous: n agents, n targets, any agent can be assigned to any target
- non-anonymous: n agents, n targets, each agent is assigned a (pre-defined) target
- TAPF (Combined Target Assignment and Path Finding)
- Proposed in [2]: teams of robots
- Multiple teams of robots (objects: only robots and the map)
- Targets assigned to teams (constraint: one robot - one target)
- Collision free paths for robots to targets (no swapping), with minimal maxspan
- GTAPF (Generalized-TAPF)
- Proposed in [3], inspired by online store order fulfilling requirements
- Order #1
- “Vintage LEGO Kit” and “Programming LEGO”
- Rush order: 2/1/2019
- Order #2
- “Vintage LEGO Kit” and “Dancing with the Stars video”
- International shipping
- requirements
- Group: an order might contain many items
- Deadline: each order needs to be accomplished before a timestamp
- Checkpoint: to fulfill certain item, some checkpoint needs to be visited
- Multiple teams of robots (same as TAPF).
- Sets of orders (multiple targets for an order, #robots 6= #orders possible)
- Checkpoints for robots/teams (certain locations must be visited before targets)
- Deadlines for orders.
- Group completion (one order at a time).
- Collision free paths for robots to targets, with minimal maxspan.
- ASP-based(Answer Set Programming) solutions.
- Others
- inspired by real-world applications, di↵erent considerations:
- Continuous vs. discrete movement
- Online vs. offine
- Checkpoints not to be (can be) revisited
- Suboptimal solutions vs. scalability
- Complex actions: transfers of items/targets between robots when pickup/putdown actions are considered
- Multi-dimensional G-TAPF: on the ground (two dimensions, cars) vs. in the air (three dimensions, drones)
10. ASPRILO
- Standardized benchmark domains
- Concise problem specification
- Domains ranging from MAPF to full order fulfillment
- Formal specification
- Formal elaboration(精心制作)
- Correctness, completeness, optimality
- Versatile instance generator
- Rich set of customization options
- Leverages(杠杆作用) multi-shot ASP for generation
- Visualizer for problems and (candidate) solutions
- Animated playback of plans
- Graphical editor for instances
- Solution checker with error feedback
- Specific error descriptions
- Modular design, easily extensible
- Reference ASP encodings
- High-level, elaboration-tolerant
- Test bed for ASP and KRR technology
11. Conclusion
- A real-world multi-agent application
- A very challenging multi-agent planning problem
- No clear dominant approach (yet)
- Search-based vs. constraints programming vs. SAT vs..
- Execution is bound to differ from the plan (integration…)
- Challenge: MAPF with Self-Interested Agents
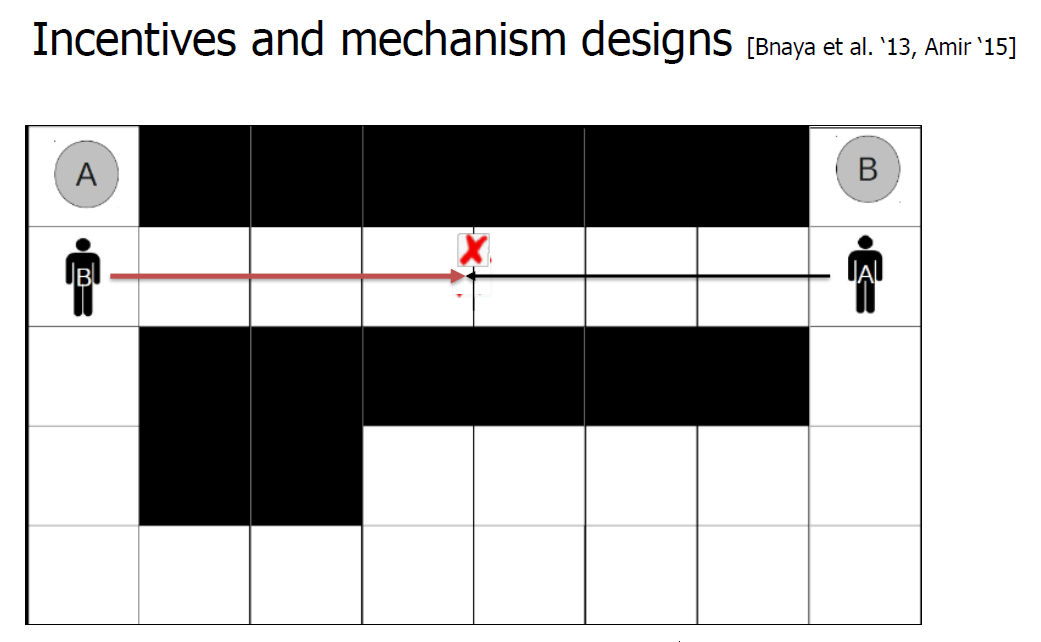
- Incentives and mechanism designs [Bnaya et al. ‘13, Amir ‘15]
- What if the other agent is adversarial(对立的)? or even worse, a human?
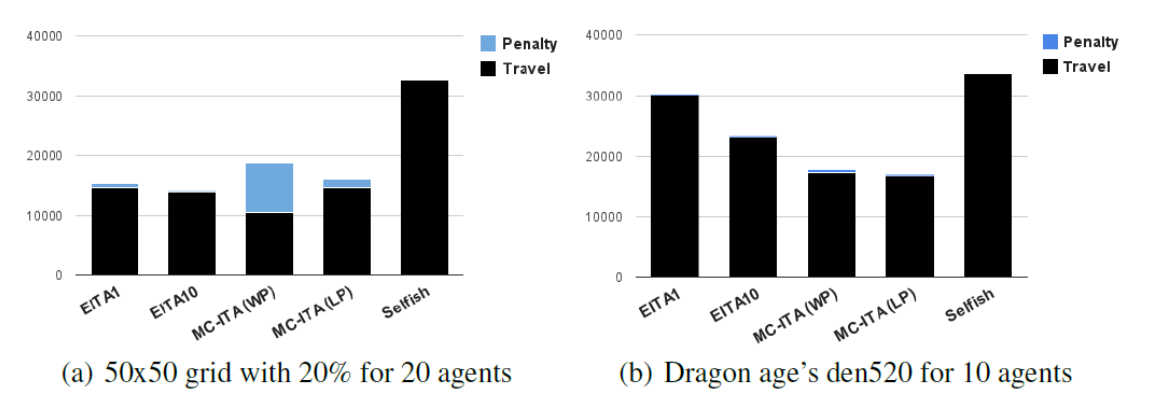
- Challenges: Applying MAPF for Real Problems
- Robotics
- Kinematic constraints (Ma et al. ‘16)
- Uncertainty is a first-class citizen
- Continuous configuration space
- Any-angle motion [Yakovlav et al. ‘17]
- Traffic management
- Flow-based approaches
- No collisions, only traffic jams
- Scale
- Challenge: MAPF as Part of a System
- Task allocation
- Pick up and delivery tasks
- Online settings
- Challenge: Relation to General Multi-Agent Planning
- Cross fertilization((무엇을 발전시키기 위해 다른 분야의 생각들을) 받아들이다) seems natural
- MAPF is a special case of MAP
- MAP
- Many models, rich literature
- Much work on uncertainty
- Poor scaling
- MAPF
- Fewer models, growing literature
- Not much work on uncertainty
- Scales well
Reference: postassco
REDUCTION-BASED SOLVERS
- How to exploit knowledge of others for solving own problems?
- by translating the problem P to another problem Q (문제를 바꾼다)
- Why is it useful?
- If anybody improves the solver for Q then we get an improved solver for P for free
- Staying on the shoulders of giants
- Reduction, compilation, re-formulation techniques
- Boolean satisfiability
- fast SAT solvers
- Constraint programming
- global constraints for pruning(修剪树枝) search space
- Answer set programming
- declarative(陈述的) framework
- Combinatorial auctions
- a Boolean satisfiability (SAT)
1. Introduction to SAT
- Express (model) the problem as a SAT formula in a conjunctive normal form (CNF)
- a Boolean satisfiability (SAT)
Boolean variables (true/false values) clause = a disjunction(分离) of literals (variables and negated(使无效) variables) formula = a conjunction of clauses solution = an instantiation of variables such that the formula is satisfied
Example:
(X or Y ) and (not X or not Y)
[exactly one of X and Y is true]
- SAT model is expressed as a CNF formulaConjunctive normal form
- We can go beyond CNF and use abstract expressions that are translated to CNF
- We can even use numerical variables (and constraints).
2. SAT encoding: core idea
- In MAPF, we do not know the lengths of plans (due to possible re-visits of nodes)!
- We can encode(把…译成电码) plans of a known length using a layered graph (temporally extended graph).
- Each layer corresponds to one time slice and indicates positions of agents at that time
3. SAT encoding with all-different
- Uses multi-valued state variables (logarithmic encoding) encoding position of agents in layers (∧ = And, ∨ = OR)
- Agent waits or moves to a neighbor
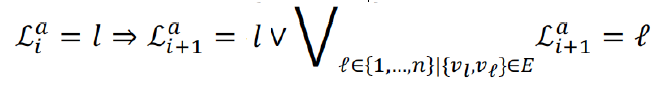
- No-train constraint
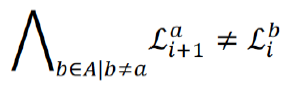
- Agents are not at the same nodes
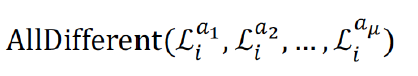
4. Direct SAT encoding
- Directly encodes positions of agents in layers
- Agent is placed at exactly one node in each layer (¬ 논리 부정)
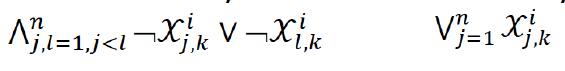
- No two agents are placed at the same node in each layer
- Agent waits or moves to a neighbor
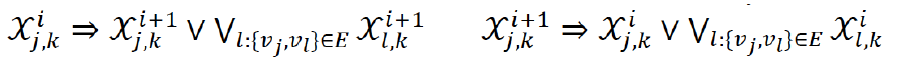
- No-swap and no-train (nodes before and after move are empty)
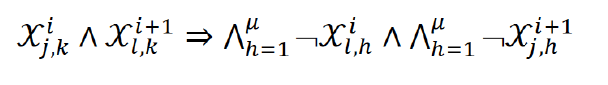
5. Comparison of SAT encodings
Finding makespan optimal solutions
(composition with Independence Detection (OD+ID))
6. Mixed model
- Using layered graph describing agent positions at each time step
- $B_tav$ : agent a occupies vertex(顶点) v at time t
- Constraints:
- each agent occupies exactly one vertex at each time
- no two agents occupy the same vertex at any time.
- if agent a occupies vertex v at time t, then a occupies a neighboring vertex or stay at v at time t + 1.
- each agent occupies exactly one vertex at each time
- Preprocessing:
- $B_tav$ = 0 if agent a cannot reach vertex v at time t or a cannot reach the destination being at v at time t
import sat
def path (N,As):
K = len(As)
lower_upper_bounds(As,LB,UB) # Incremental generation of layers
between(LB,UB,M),
B = new_array(M+1, K,N),
B :: 0..1,
% Initialize the first and last states(Setting the initial and destination locations)
foreach(循环) (A in 1..K)
(V,FV) = As[A]
B[1,A,V] = 1,
B[M+1,A,FV] = 1
end,
% Each agent occupies exactly one vertex
foreach(T in 1..M+1, A in 1..K)
sum([B[T,A,V]] : V in 1..N) #=1
end,
% No two agents occupy the same vertex (No Conflict between agents)
foreach ( T in 1..M+1, V in 1..K)
sum([B[T,A,V] : A in 1..K]) # =1
% Every Transition is valid(Agent moves to a neighboring vertex)
foreach (T in 1..M, A in 1..K, V in 1..N)
neibs(V,neibs),
B[T,A,V] # =>
sum([B[T+1, A, U]: U in neibs]) #>= 1
end,
% K-robustness
foreach(T in 1..M1, A in 1..K, V in 1..N)
B[T,A,V] # => sum([B[Prev,A2,V]:
A2 in 1..K, A2!=A
prev in max(1,T-L)..T]) # = 0
end,
solve(B)
output_plan(B)
- Picat provides assignment and loop statements for programming everyday things.
- a Boolean satisfiability (SAT)
- Assembly Sequence Planning (ASP)
7. Objectives in SAT
- Makespan (minimize the maximum end time)
- incrementally add layers until a solution found
- Sum of cost (minimize the sum of end times)
- incrementally add layers and look for the SOC optimal solution in each iteration (makespan + SOC optimal)
- generate more layers (upper bound) and then optimize SOC (naïve)
- incrementally add layers and increase the cost limit until a solution is found [Surynek et al, ECAI 2016]
8. Real World
- Objective
- How to develop robust and scalable AI technology for dealing with complex dynamic application scenarios?
- What’s needed?
- a model scenario
- Robotic intra-logistics (물류)
- why?
- rich : multi-faceted, full of variations
- scalable : layout, objects, granularity(粒度)
- measurable : makespan, energy, quality of service
- integrative(综合的) : mapf, data, constraints, decisions
- relevant : industry 4.0
- Robotics systems for logistics(物流) and warehouse automation based on many mobile robots and movable shelves
- Main tasks: order fulfillment(routing(路由), order picking, replenishment(补充))
- Many competing industry solutions : Amazon, Dematic, Genzebach, Gray Orange, Swisslog
- what’s in the environment?
- Objects : floor, robots, shelves, products, people, etc
- Relations : positions, carries/d, capacity, orientation, durations, etc
- Actions : move, pickup, putdown, pick, charge, restock, etc.
- Objectives : deadlines, throughput, exploitation, energy management, human machine interaction, etc.
9. Beyond MAPF
- Classified by objects, measurability, constraints, decisions
- MAPF (Multi-Agent Path Finding)
- Most simple, straightforwards extension of APF
- Objects: only robots and the map
- anonymous: n agents, n targets, any agent can be assigned to any target
- non-anonymous: n agents, n targets, each agent is assigned a (pre-defined) target
- TAPF (Combined Target Assignment and Path Finding)
- Proposed in [2]: teams of robots
- Multiple teams of robots (objects: only robots and the map)
- Targets assigned to teams (constraint: one robot - one target)
- Collision free paths for robots to targets (no swapping), with minimal maxspan
- GTAPF (Generalized-TAPF)
- Proposed in [3], inspired by online store order fulfilling requirements
- Order #1
- “Vintage LEGO Kit” and “Programming LEGO”
- Rush order: 2/1/2019
- Order #2
- “Vintage LEGO Kit” and “Dancing with the Stars video”
- International shipping
- requirements
- Group: an order might contain many items
- Deadline: each order needs to be accomplished before a timestamp
- Checkpoint: to fulfill certain item, some checkpoint needs to be visited
- Multiple teams of robots (same as TAPF).
- Sets of orders (multiple targets for an order, #robots 6= #orders possible)
- Checkpoints for robots/teams (certain locations must be visited before targets)
- Deadlines for orders.
- Group completion (one order at a time).
- Collision free paths for robots to targets, with minimal maxspan.
- ASP-based(Answer Set Programming) solutions.
- Others
- inspired by real-world applications, di↵erent considerations:
- Continuous vs. discrete movement
- Online vs. offine
- Checkpoints not to be (can be) revisited
- Suboptimal solutions vs. scalability
- Complex actions: transfers of items/targets between robots when pickup/putdown actions are considered
- Multi-dimensional G-TAPF: on the ground (two dimensions, cars) vs. in the air (three dimensions, drones)
- inspired by real-world applications, di↵erent considerations:
- MAPF (Multi-Agent Path Finding)
10. ASPRILO
- Standardized benchmark domains
- Concise problem specification
- Domains ranging from MAPF to full order fulfillment
- Formal specification
- Formal elaboration(精心制作)
- Correctness, completeness, optimality
- Versatile instance generator
- Rich set of customization options
- Leverages(杠杆作用) multi-shot ASP for generation
- Visualizer for problems and (candidate) solutions
- Animated playback of plans
- Graphical editor for instances
- Solution checker with error feedback
- Specific error descriptions
- Modular design, easily extensible
- Reference ASP encodings
- High-level, elaboration-tolerant
- Test bed for ASP and KRR technology
11. Conclusion
- A real-world multi-agent application
- A very challenging multi-agent planning problem
- No clear dominant approach (yet)
- Search-based vs. constraints programming vs. SAT vs..
- Execution is bound to differ from the plan (integration…)
- Challenge: MAPF with Self-Interested Agents
- Incentives and mechanism designs [Bnaya et al. ‘13, Amir ‘15]
- What if the other agent is adversarial(对立的)? or even worse, a human?
- Challenges: Applying MAPF for Real Problems
- Robotics
- Kinematic constraints (Ma et al. ‘16)
- Uncertainty is a first-class citizen
- Continuous configuration space
- Any-angle motion [Yakovlav et al. ‘17]
- Traffic management
- Flow-based approaches
- No collisions, only traffic jams
- Scale
- Robotics
- Challenge: MAPF as Part of a System
- Task allocation
- Pick up and delivery tasks
- Online settings
- Challenge: Relation to General Multi-Agent Planning
- Cross fertilization((무엇을 발전시키기 위해 다른 분야의 생각들을) 받아들이다) seems natural
- MAPF is a special case of MAP
- MAP
- Many models, rich literature
- Much work on uncertainty
- Poor scaling
- MAPF
- Fewer models, growing literature
- Not much work on uncertainty
- Scales well
Reference: postassco
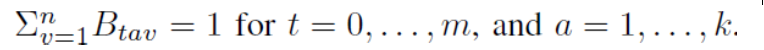
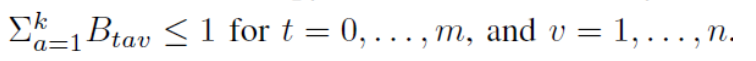
Comments