Euclidean & Topology
08 Apr 2021 | ROBOTICS
로보틱스나 컴퓨터 비전을 공부하다 보면 가끔 햇갈린다. 그래서 다시 한번 내 나름대로(?) 정리를 해보았다.
로봇틱스를 공부를 하면서
Euclidean은 이미지 같은 2D(직선좌표) 같은 곳에 많이 쓰이고
Toplogy는 슬램으로 따지면 만들어진 3D map으로 표현된것이라고 생각을 했다.(즉 사람이 살고 있는 공간)
그러나.
Topology is a kind of math, in which we study shapes – but we pretend that all the shapes we deal with are made of really squishy rubber. This is particularly useful for studying crazy shapes, like high-dimensional objects or weird, twisty knots.
메비우스의 띠가 대표적인 예 이다.
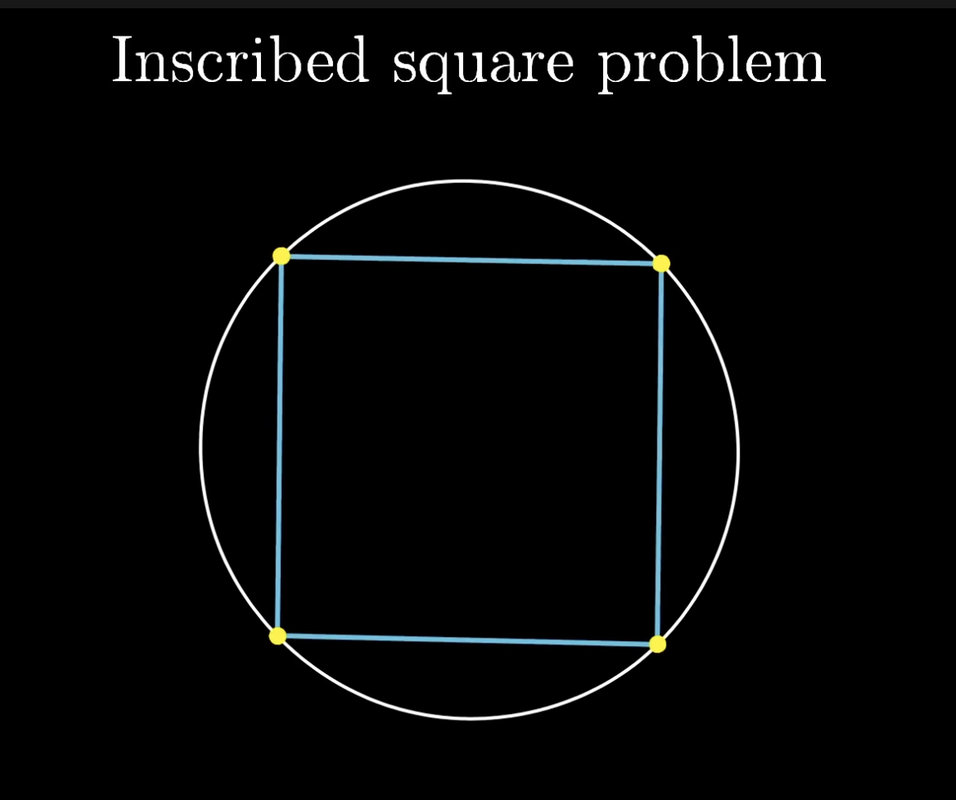
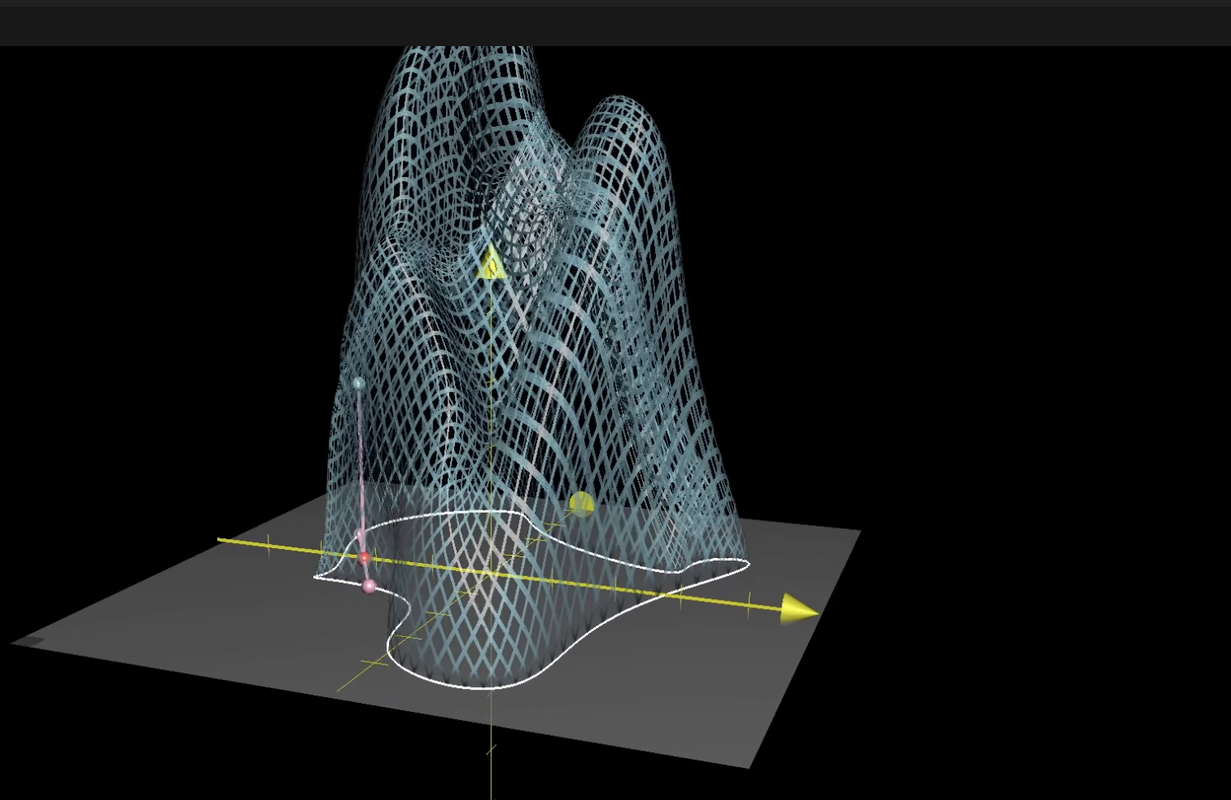
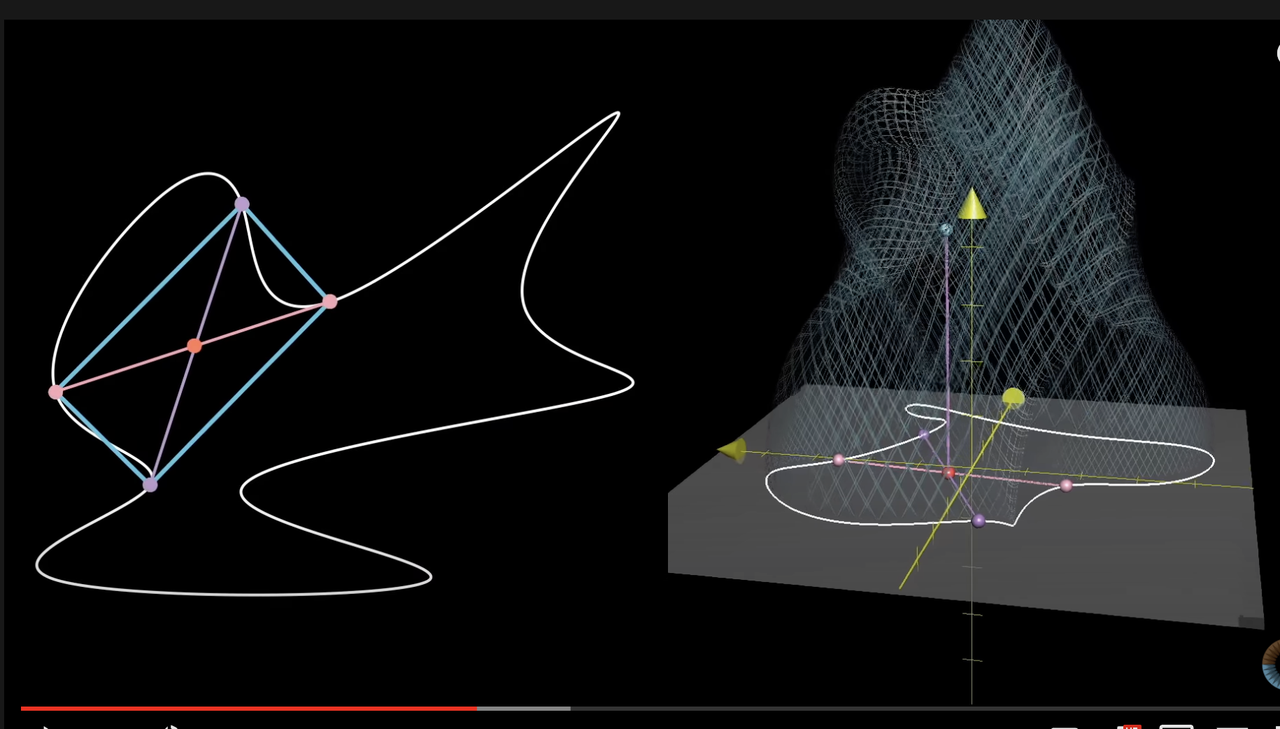
그리고 직사각형 툴(?) 방식으로 두 직선의 쌍이 교차하는 중간점으로 만나게 되는데. 이 만나게 되는 점을, 모델의 중심이라고 부른다(즉, 도넛, 컵 같이 생긴 형상을 가지고 정의하는 것이 아니라 직사각형 툴 방식으로 물체를 수학적으로 정의한다.)
아래와 같이 표현이 되며, 그렇기 떄문에 도넛이든 컵이든 모든 것은 하나의 홀로 만들어진 연속적이기 때문에, 수학적인 shape만 신경 쓴다.
Topology는 3D Geometry를 만들때 많이 쓰인다. (예, 3D 모델을 만들거나, 슬램의 맵을 만들때 )
https://www.youtube.com/watch?v=VudCtEtNXbI
로보틱스나 컴퓨터 비전을 공부하다 보면 가끔 햇갈린다. 그래서 다시 한번 내 나름대로(?) 정리를 해보았다.
로봇틱스를 공부를 하면서
Euclidean은 이미지 같은 2D(직선좌표) 같은 곳에 많이 쓰이고
Toplogy는 슬램으로 따지면 만들어진 3D map으로 표현된것이라고 생각을 했다.(즉 사람이 살고 있는 공간)
그러나.
Topology is a kind of math, in which we study shapes – but we pretend that all the shapes we deal with are made of really squishy rubber. This is particularly useful for studying crazy shapes, like high-dimensional objects or weird, twisty knots.
메비우스의 띠가 대표적인 예 이다.
그리고 직사각형 툴(?) 방식으로 두 직선의 쌍이 교차하는 중간점으로 만나게 되는데. 이 만나게 되는 점을, 모델의 중심이라고 부른다(즉, 도넛, 컵 같이 생긴 형상을 가지고 정의하는 것이 아니라 직사각형 툴 방식으로 물체를 수학적으로 정의한다.)
아래와 같이 표현이 되며, 그렇기 떄문에 도넛이든 컵이든 모든 것은 하나의 홀로 만들어진 연속적이기 때문에, 수학적인 shape만 신경 쓴다.
Topology는 3D Geometry를 만들때 많이 쓰인다. (예, 3D 모델을 만들거나, 슬램의 맵을 만들때 )
https://www.youtube.com/watch?v=VudCtEtNXbI



Comments