SLAM에서 최적화를 할때 Log LikelyHood를 통한 error Function(Object Function)을 만들고 미지수에 대해 최적화를 하여 값을 구한다.

각 노드간에 연결되어 있는 constraints에 대하여 Gaussian Distribution으로 나타내게 되면 unimodel형식이며

이에 대한 각 노드간에 연결되어 있는 constraints값을 통해 error function을 정의하여서 Gaussian Newton이나 LM 방법을 사용을 하여서 Non Linear System에 대한 Optimization을 한다.

허나, GPS의 튀는 값으로 잘못된 edge가 연결이 되거나 Descriptor Matching을 통해 잘못 loop closure가 일어날 경우, 맵이 쉽게 일그러진다.

즉, node간에 잘못된 constraints가 생기게 된다면, 위와 같이 multi model gaussian distributions 형상이 나오는데, 이에 대한 Object Function에 대해 Optimization를 하게 된다면, Error가 점점 커지기 때문이다.

이에 생겨난게 Max Mixture 이다.

Max Mixture

Max Mixture는 이 두 multi model을 가지고 있는 Object function중에 Maximum LikelyHood를 가지고 있는 Constraints과 edge만 가지고 Least Square, Optimization을 하겠다라는 의미이다.

Multi Model를 구하고 Object Function을 만드는 방법은 다음과 같다.

먼저 Multi model을 구하는 것은 아래와 같다.

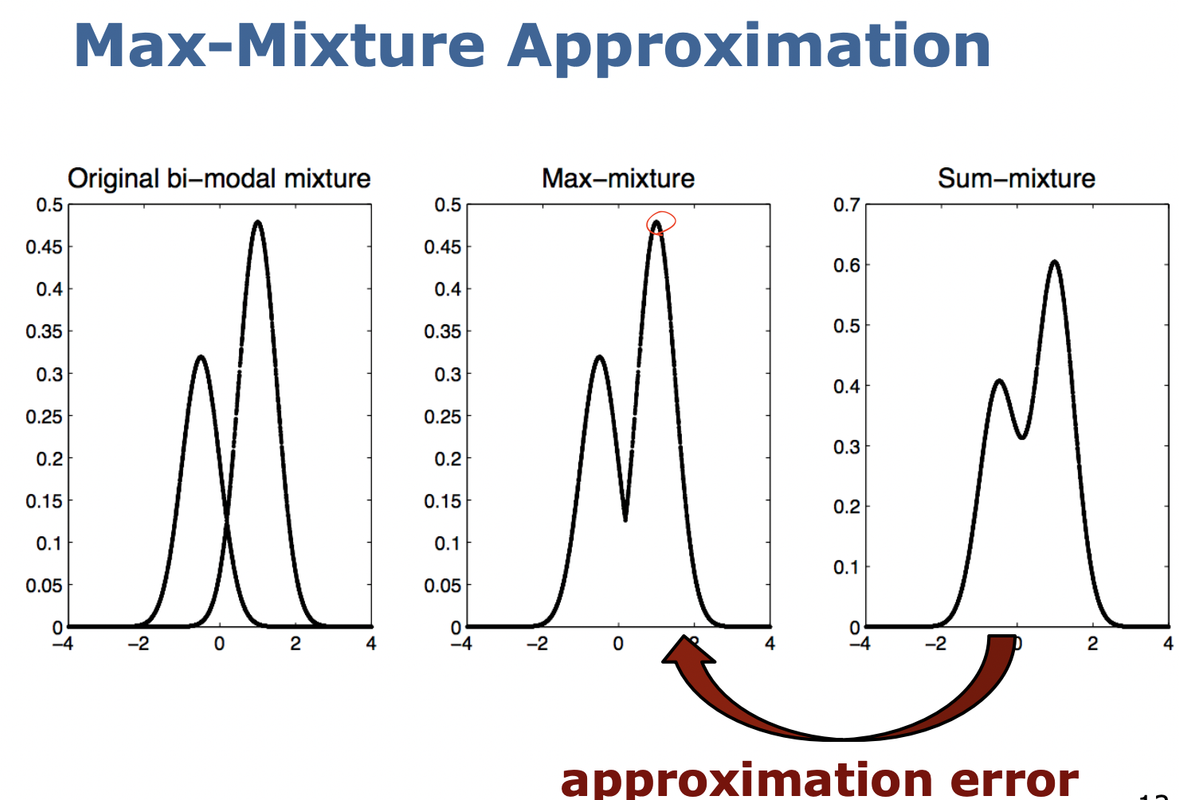
Multi Model을 만들고 error function을 만들어 Optimization을 해야하기에 log likleyhood를 사용하지만, Sum은 Log LikelyHood에 들어갈 수없는데, 그 이유는 값이 Negative(-) 값이 나오기 때문이다.

이에 Sum of Gaussian Distribution이 아닌, Maximum of Gaussian을 하여서 Multi Model을 만든다.

Max Mixture Robust Pose Graph

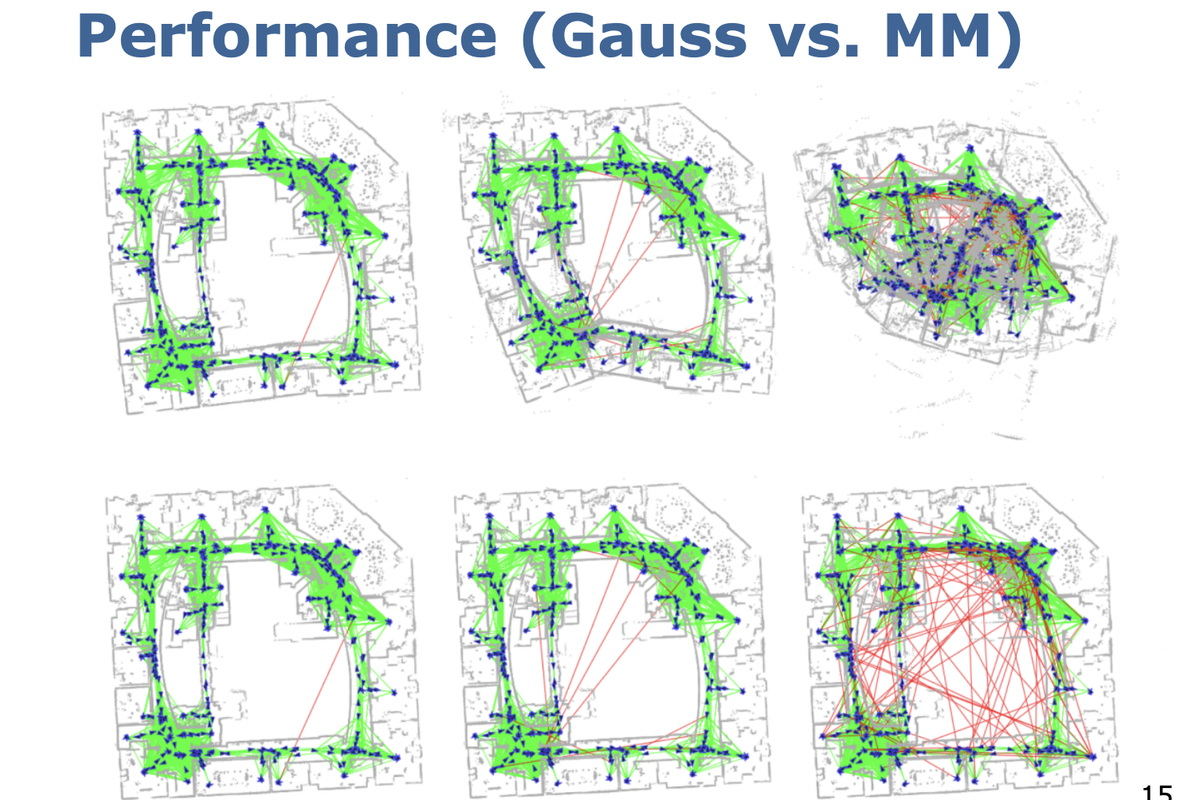
이렇게 multi model을 구할 수 있지만, Max Mixture Robust Pose Graph에서는 전체 노드와 constraints중 Maximum LikelyHood를 가지고 있는 노드와 constraints을 가지고 object function을 써서 Optimization을 하는 것이다. Iteration을 할때 Maximum LikelyHood를 가지는 node들과 constraints의 object function으로 최적화를 한다.

코드는 아래와 같다.

void EdgeSE2Mixture::UpdateBelief(int i)
{
  //required for multimodal max-mixtures, for inlier/outliers the vertices would not change
  this->setVertex(0,allEdges[i]->vertex(0));
  this->setVertex(1,allEdges[i]->vertex(1));           

  double p[3];
  allEdges[i]->getMeasurementData(p);
  this->setMeasurement(g2o::SE2(p[0],p[1],p[2]));
  this->setInformation(allEdges[i]->information());  
}

//get the edge with max probability
void EdgeSE2Mixture::computeError()
{
  int best = -1;
  double minError = numeric_limits<double>::max();
  for(unsigned int i=0;i<numberComponents;i++){    
    double thisNegLogProb = getNegLogProb(i);
    if(minError>thisNegLogProb){
      best = i;
      minError = thisNegLogProb;
    }
  }

  bestComponent = best;
  UpdateBelief(bestComponent);
  //cerr << "\nBest component is "<<bestComponent<<"\n";

  //this will be used by the optimizer
  g2o::EdgeSE2::computeError();
}

double EdgeSE2Mixture::getNegLogProb(unsigned int c)
{  
  allEdges[c]->computeError();
  //cerr << "\nchi2 for " <<c<<" "<< allEdges[c]->chi2();
  return -log(weights[c]) +
	  0.5*log(determinants[c]) +
	  0.5*allEdges[c]->chi2();
}

pick one well made unimodel Gaussian model, with that use it as object function(cost function) to do optimization iteratively.(Iteratively pick best uni-model Gaussian model)

Switchable constraints

Switchable constraints로 마찬가지다, node간에 잘못된 constraints을 무시를하여서 Optimization을 하는데 목적이다.

Reference

Least Square Deep Explain

Robust Pose Graph

MAX-MIXTURE CODE

Switchable Constraint CODE

OPENSLAM CODE