2. 3D Rigid Body Transform
02 Jun 2020 | Visual SLAM
강체 변환
- 강체(Rigid Body)
- 강체 : 딱딱한 물체 -> 물체의 형태가 변하지 않음을 말함.
좌표계
- 왼손 좌표계 & 오른손 좌표계(3차원 공간)
- 위치나 방향을 나타내려고 할때 기준점과 기준 방향이 필요
- 두 가지의 방식의 좌표계가 존재 => 왼손 & 오른손 좌표계
- 두 좌표계는 아무리 회전을 해도 절대 동일해 지지 않음
- 나머지 소위 좌표계라고 착각되는 것들은 모두 회전 변환으로 상호 변환이 가능함
- 책인용 : “왼손 시스템의 세 번째 축은 오른손 시스템과 반대방향이다.”
벡터 및 스칼라
- Scalar(스칼라)
- 양 (하나의 값) 및 크기를 말한다(Scale)
- Vector
- 방향과 크기를 가짐
- 위치는 없음
- 벡터와 벡터간 연산 : 덧셈, 뺄셈, 외적(결과는 벡터), 내적(결과는 스칼라)
- 벡터와 스칼라 연산: 곱셈(결과는 벡터)
- Position
- 위치만 가짐
- 위치와 위치간 연산 : 뺄셈 ( 결과는 벡터 )
- 벡터와 위치 연산 : 덧셈 ( 결과는 위치 )
- 3D 벡터와 3D 위치의 공통점
- X, Y, Z 값으로 표시 가능
- 하지만 둘의 차이점을 아는 것은 중요
내적
- 벡터들간의 Projection 관계를 나타낸다(projection 길이를 구할 수 있다)
좌표계
- e는 선형성을가지고 있는 공간상의 bias, a는 벡터
- 좌표축간에 회전을 알 수 있다.
외적
- 3D 강체 운동에서 외적은 Rotation을 구할 수 있다.
- Skew-symmetric, 부호 ^
Rotation Matrix
- p 는 카메라의 벡터
- 카메라 운동은 강체 운동이다, 이것은 똑같은 벡터와 각종 좌표계의 길이와 각도가 변환이 되지 않는 것을 보장한다.
- 즉, 이것을 오일러 변환이라고 말한다(euler transformation)
- 예를 들어 (e_1, e_2, e_3)를 가지고 있는 어떤 단위가 1번의 Transformation을 거치면, (e_1’, e_2’, e_3’)가 된었다고 할때, 똑같은 벡터 a 를 이용하여 두 좌표계 [a_1,a_2,a_3]^T 와 [a_1’,a_2’,a_3’]^T 를 만들수 있다.
- 좌표계의 정의에 근거하면
- 두 관계를 묘사하였고, (e_1, e_2, e_3)를 반대편에다 대입하였을 경우, 아래와 같은 단위 매트릭스를 구할 수 있게 된다
- 여기서 R은 Rotation Matrix라고 불린다.
- Rotation Matrix의 특징은 Determinant가 항상 1이라는 것이다. 그렇기 때문에 아래와 같이 정의할 수 있다.
- SO(n)은 Special Orthogonal Group이라고 하여 Li group이라고 말한다.
- n Demension의 Rotation Matix의 집합으로부터 구성이 되어 있다.
- 특히, SO(3) 은 3차원 공간의 Rotation을 말한다.
- Rotation Matrix는 Camera의 Rotatation으로 묘사할 수 있다.
오일러 변환(euler Transformation)
- 오일로 변환중에 Rotation Matrix를 제외한 이동인(transportation) T가 있다.
- 만약 World 좌표계에서의 벡터 a, 그리고 한번의 Rotation과 이동 T가 있었다면, 아래와 같이 a’ 를 얻을 수 있다.
Transformation Matrix and Homogeneous coordinate
- 방금 위에서 공부한 것들을 이용하여서 아래와 같이 방정식으로 쉽게 만들 수 있다.
- T는 Transformation이라고 불린다.
- 이와 같은 표현 방법을 Homogeneous Coordinate 불리는데 그래픽스 또는 3D 비전 분야에서 많이 사용 되는 좌표계의 한 종류이다.
- 인간이 보고 있는 좌표계는 Inhmogeous 이다.
- Homogeneous를 이용한다면 무한대의 점을 표현하는데 유리하다
- Homogeneous 좌표계를 사용하면 Affine 변환과 Perspective 변환이 하나의 행렬로 정의 할 수 있다.
- 선의 Homogeneous coordinate 표현
- 직선의 방정식 ax+by+c = 0 을 ax+by+cw=0로 표현한다.
- 이때 ax+by+c = 0 상의 점으로 투영되는 점 (x,y,w)들은 ax+by+cw를 만족해야 한다.
- 점의 Homogeneous coordinate 표현
- 임의 상수 w에 대해 점 P(x,y)의 좌표를 P(wx,wy,w)로 표현하는 방식이다.
- 2D 이미지에서 한 점으로 투영되는 모든 점(같은 ray 상의 점)들을 표현 할 수 있다(Up to Scale)
- 원래 좌표를 구하고 싶다면 w=1로 만들면 된다. P(x,y,1)
- 이와 같은 Transformation 매트릭스를 Special Euclidean Group(SE)으로 불린다.
- SO(3) 는 Rotation Matrix를 묘사하고, SE는 Transformation을 묘사한다.
하지만 오일러 변환을 사용하는 경우 짐벌락(black hole처럼 singularity에 빠지는 경우) 문제 발생
- 오일러 변환을 사용하는 경우 짐벌락 문제 Blcak hole 처럼 Signgularity에 빠지는 경우가 나타나게 됨
- 이는 Full Matrix를 사용하여 SO 구하게 되면, 많은 Computational을 제공할 뿐만 아니라 Singularity에 빠지기 쉽다.
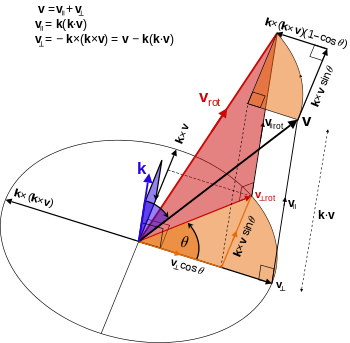
Axis-Angle, Rodriguerese Formular
- 그렇기 떄문에 SO(3)를 더 간편하게 구하기 위해 Rodriguerese Formular를 쓴다.
- 주어진 축(Axis)와 Angle of Rotation으로 Rotation Vector값으로 3D rotation을 구할 수있다.
- 구해진 Rotatation vector값을 Rodrigues 수식에 따라 행렬로 변환한다.
- By extension, this can be used to transform all three basis vectors to compute a rotation matrix in SO(3)
- the Rodrigues’ formula provides an algorithm to compute the exponential map from so(3), the Lie algebra of SO(3), to SO(3) without actually computing the full matrix exponential.
Reference
SLAM KR
视觉SLAM书
Cmake Tutorial : https://github.com/TheErk/Cmake-tutorial.
Wiki
강체 변환
- 강체(Rigid Body)
- 강체 : 딱딱한 물체 -> 물체의 형태가 변하지 않음을 말함.
좌표계
- 왼손 좌표계 & 오른손 좌표계(3차원 공간)
- 위치나 방향을 나타내려고 할때 기준점과 기준 방향이 필요
- 두 가지의 방식의 좌표계가 존재 => 왼손 & 오른손 좌표계
- 두 좌표계는 아무리 회전을 해도 절대 동일해 지지 않음
- 나머지 소위 좌표계라고 착각되는 것들은 모두 회전 변환으로 상호 변환이 가능함
- 책인용 : “왼손 시스템의 세 번째 축은 오른손 시스템과 반대방향이다.”
벡터 및 스칼라
- Scalar(스칼라)
- 양 (하나의 값) 및 크기를 말한다(Scale)
- Vector
- 방향과 크기를 가짐
- 위치는 없음
- 벡터와 벡터간 연산 : 덧셈, 뺄셈, 외적(결과는 벡터), 내적(결과는 스칼라)
- 벡터와 스칼라 연산: 곱셈(결과는 벡터)
- Position
- 위치만 가짐
- 위치와 위치간 연산 : 뺄셈 ( 결과는 벡터 )
- 벡터와 위치 연산 : 덧셈 ( 결과는 위치 )
- 3D 벡터와 3D 위치의 공통점
- X, Y, Z 값으로 표시 가능
- 하지만 둘의 차이점을 아는 것은 중요
내적
- 벡터들간의 Projection 관계를 나타낸다(projection 길이를 구할 수 있다)
좌표계
- e는 선형성을가지고 있는 공간상의 bias, a는 벡터
- 좌표축간에 회전을 알 수 있다.
외적
- 3D 강체 운동에서 외적은 Rotation을 구할 수 있다.
- Skew-symmetric, 부호 ^
Rotation Matrix
- p 는 카메라의 벡터
- 카메라 운동은 강체 운동이다, 이것은 똑같은 벡터와 각종 좌표계의 길이와 각도가 변환이 되지 않는 것을 보장한다.
- 즉, 이것을 오일러 변환이라고 말한다(euler transformation)
- 예를 들어 (e_1, e_2, e_3)를 가지고 있는 어떤 단위가 1번의 Transformation을 거치면, (e_1’, e_2’, e_3’)가 된었다고 할때, 똑같은 벡터 a 를 이용하여 두 좌표계 [a_1,a_2,a_3]^T 와 [a_1’,a_2’,a_3’]^T 를 만들수 있다.
- 좌표계의 정의에 근거하면
- 두 관계를 묘사하였고, (e_1, e_2, e_3)를 반대편에다 대입하였을 경우, 아래와 같은 단위 매트릭스를 구할 수 있게 된다
- 여기서 R은 Rotation Matrix라고 불린다.
- Rotation Matrix의 특징은 Determinant가 항상 1이라는 것이다. 그렇기 때문에 아래와 같이 정의할 수 있다.
- SO(n)은 Special Orthogonal Group이라고 하여 Li group이라고 말한다.
- n Demension의 Rotation Matix의 집합으로부터 구성이 되어 있다.
- 특히, SO(3) 은 3차원 공간의 Rotation을 말한다.
- Rotation Matrix는 Camera의 Rotatation으로 묘사할 수 있다.
오일러 변환(euler Transformation)
- 오일로 변환중에 Rotation Matrix를 제외한 이동인(transportation) T가 있다.
- 만약 World 좌표계에서의 벡터 a, 그리고 한번의 Rotation과 이동 T가 있었다면, 아래와 같이 a’ 를 얻을 수 있다.
Transformation Matrix and Homogeneous coordinate
- 방금 위에서 공부한 것들을 이용하여서 아래와 같이 방정식으로 쉽게 만들 수 있다.
- T는 Transformation이라고 불린다.
- 이와 같은 표현 방법을 Homogeneous Coordinate 불리는데 그래픽스 또는 3D 비전 분야에서 많이 사용 되는 좌표계의 한 종류이다.
- 인간이 보고 있는 좌표계는 Inhmogeous 이다.
- Homogeneous를 이용한다면 무한대의 점을 표현하는데 유리하다
- Homogeneous 좌표계를 사용하면 Affine 변환과 Perspective 변환이 하나의 행렬로 정의 할 수 있다.
- 선의 Homogeneous coordinate 표현
- 직선의 방정식 ax+by+c = 0 을 ax+by+cw=0로 표현한다.
- 이때 ax+by+c = 0 상의 점으로 투영되는 점 (x,y,w)들은 ax+by+cw를 만족해야 한다.
- 점의 Homogeneous coordinate 표현
- 임의 상수 w에 대해 점 P(x,y)의 좌표를 P(wx,wy,w)로 표현하는 방식이다.
- 2D 이미지에서 한 점으로 투영되는 모든 점(같은 ray 상의 점)들을 표현 할 수 있다(Up to Scale)
- 원래 좌표를 구하고 싶다면 w=1로 만들면 된다. P(x,y,1)
- 이와 같은 Transformation 매트릭스를 Special Euclidean Group(SE)으로 불린다.
- SO(3) 는 Rotation Matrix를 묘사하고, SE는 Transformation을 묘사한다.
하지만 오일러 변환을 사용하는 경우 짐벌락(black hole처럼 singularity에 빠지는 경우) 문제 발생
- 오일러 변환을 사용하는 경우 짐벌락 문제 Blcak hole 처럼 Signgularity에 빠지는 경우가 나타나게 됨
- 이는 Full Matrix를 사용하여 SO 구하게 되면, 많은 Computational을 제공할 뿐만 아니라 Singularity에 빠지기 쉽다.
Axis-Angle, Rodriguerese Formular
- 그렇기 떄문에 SO(3)를 더 간편하게 구하기 위해 Rodriguerese Formular를 쓴다.
- 주어진 축(Axis)와 Angle of Rotation으로 Rotation Vector값으로 3D rotation을 구할 수있다.
- 구해진 Rotatation vector값을 Rodrigues 수식에 따라 행렬로 변환한다.
- By extension, this can be used to transform all three basis vectors to compute a rotation matrix in SO(3)
- the Rodrigues’ formula provides an algorithm to compute the exponential map from so(3), the Lie algebra of SO(3), to SO(3) without actually computing the full matrix exponential.
Reference
SLAM KR 视觉SLAM书
Cmake Tutorial : https://github.com/TheErk/Cmake-tutorial.
Wiki









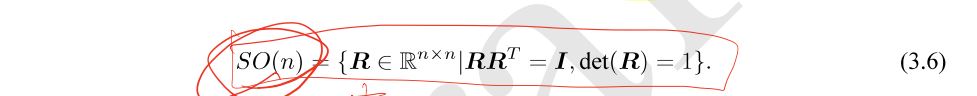






Comments