7. Lie Group and Lie Algebra 2
17 Jun 2020 | Visual SLAM
Introduction
- Reasons to Convert Lie Groups and Lie Algebra
- Study on Rigid body motion in 3D world such as rotation matrix, rotation vector, Euler angle, quaternion, etc. => Content limited to the expression of rotation
- SLAM needs to find the optimal value while updating the camera pose values including rotation and movement. In general, it is solved by solving the optimal R after minimizing t and minimizing the error after configuring the optimization problem.
- in the case of a rotation matrix, the complexity increases because there is a constraint that the determinant is an orthogonal matrix.
- When the relationship between the Lie group and the Lie algebra is used, the problem of estimating the pose of the camera is converted into an unconstrained optimization problem, which is simplified and accessible.
Sum up
- Easy access by using conversion relationship between lie group and lie algebra(as Rotation matrix and translation vector)
Example of Lie Group and Lie ALgebra
- 3D rotation matrix SO(3), transformation matrix SE(3)
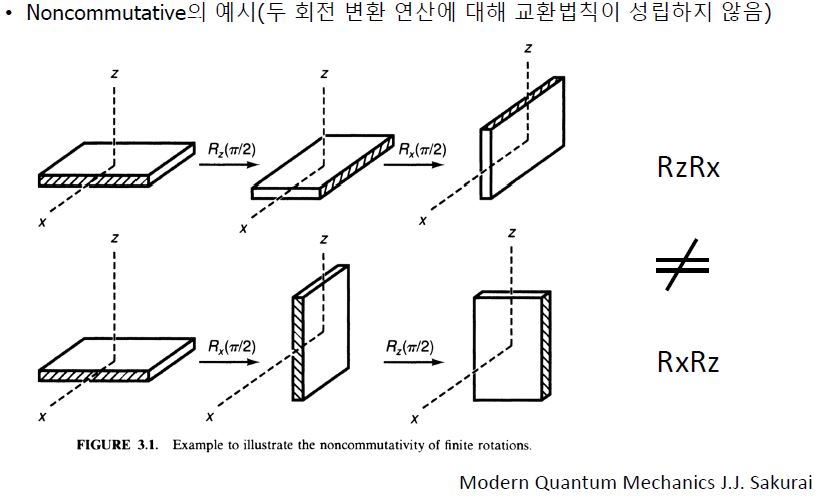
- When there are two arbitrary rotation matrices R1 and R2, if the definition of matrix addition is followed, it is no longer a rotation matrix.
- The multiplication operation corresponds to the synthesis of a rotation matrix and a transformation matrix, and the product of two rotation matrices means that two rotations are made in succession.
- Called Group only for one of these working sets
Sum up
Lie Group
- Lie group is an algebraic structure consisting of sets and operations
- Ex) When a set is called A and some operations are marked with ·, the group is represented by G = (A, ·)
- Lie group constraint
proving Lie Group
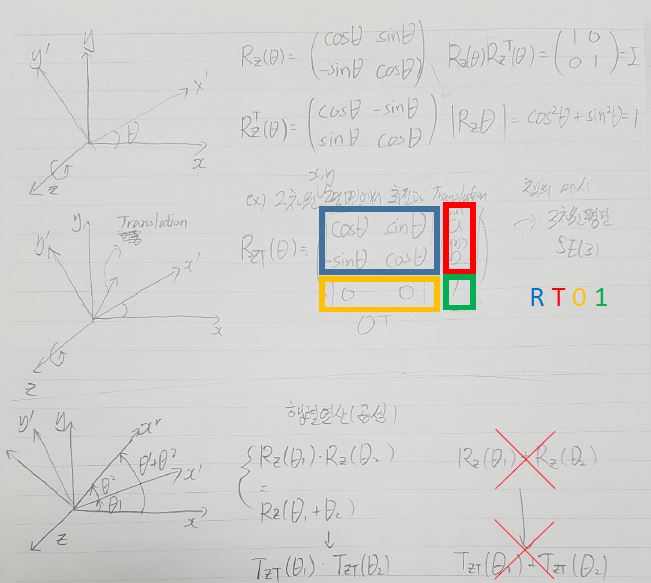
- The following properties are satisfied when only the random rotation matrix is considered
- R is a camera rotation that continuously changes with time and is expressed as a function of time R(t)
- Since it is still a rotation matrix, the following properties are satisfied
- Derivative of time on both sides of the equation (differentiation of the product) gives:
- The ^ operator converts a vector to an symmetric skew matrix. This means that any counter symmetric matrix can find the corresponding vector. By putting v we can see:
- 즉 ^ 요것일 이용하여서 벡터를 symmetric skew matrix로 표현한다. v이것은 반대로 symeetric skew matrix를 vector로 바꾸는 것이다.
- Multiply both sides of the spinning equation by R(t). Since R is an orthogonal matrix,
- Formula induction process
- If Phi(t) does not depend on time, Equation 4.8 can be written as follows to convert it to a linear differential equation.
- The above formula is the differential equation for R, and the solution of the linear differential equation is
- Approximate solution using Taylor series
- Linear differential equation solution
- 국부 미분 관계 Local differential relationship
Definition of Lie Algebra
- Each Lie group has a corresponding Lie Algebra
- Lie Algebra is a local property of Lie Group
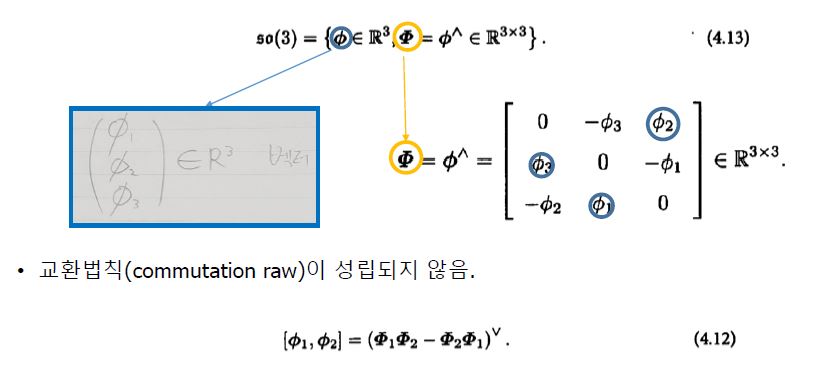
- Lie algebra consists of a vector space V, a real set F, and a two-term operation[,].
- Element notation of SO(3): (1) 3D vector and (2) 3x3 matrix can be expressed. The meanings of the two are the same, and ^ and v can be used to convert and notify matrix to vector using vector to matrix.
- Element notation of SE(3) :(1)6 dimensional vector and (2)4x4 matrix can be expressed Translation and rotatio can be expressed as rho and phi The meaning of the two is the same, and using ^ and v to matrix from vector to matrix From vector to vector and notation
<a href=https://postimg.cc/G490Jw8M”>
Reference
SLAM KR
Introduction
- Reasons to Convert Lie Groups and Lie Algebra
- Study on Rigid body motion in 3D world such as rotation matrix, rotation vector, Euler angle, quaternion, etc. => Content limited to the expression of rotation
- SLAM needs to find the optimal value while updating the camera pose values including rotation and movement. In general, it is solved by solving the optimal R after minimizing t and minimizing the error after configuring the optimization problem.
- in the case of a rotation matrix, the complexity increases because there is a constraint that the determinant is an orthogonal matrix.
- When the relationship between the Lie group and the Lie algebra is used, the problem of estimating the pose of the camera is converted into an unconstrained optimization problem, which is simplified and accessible.
Sum up
- Easy access by using conversion relationship between lie group and lie algebra(as Rotation matrix and translation vector)
Example of Lie Group and Lie ALgebra
- 3D rotation matrix SO(3), transformation matrix SE(3)
- When there are two arbitrary rotation matrices R1 and R2, if the definition of matrix addition is followed, it is no longer a rotation matrix.
- The multiplication operation corresponds to the synthesis of a rotation matrix and a transformation matrix, and the product of two rotation matrices means that two rotations are made in succession.
- Called Group only for one of these working sets
Sum up
Lie Group
- Lie group is an algebraic structure consisting of sets and operations
- Ex) When a set is called A and some operations are marked with ·, the group is represented by G = (A, ·)
- Lie group constraint
proving Lie Group
- The following properties are satisfied when only the random rotation matrix is considered
- R is a camera rotation that continuously changes with time and is expressed as a function of time R(t)
- Since it is still a rotation matrix, the following properties are satisfied
- Derivative of time on both sides of the equation (differentiation of the product) gives:
- The ^ operator converts a vector to an symmetric skew matrix. This means that any counter symmetric matrix can find the corresponding vector. By putting v we can see:
- 즉 ^ 요것일 이용하여서 벡터를 symmetric skew matrix로 표현한다. v이것은 반대로 symeetric skew matrix를 vector로 바꾸는 것이다.
- Multiply both sides of the spinning equation by R(t). Since R is an orthogonal matrix,
- Formula induction process
- If Phi(t) does not depend on time, Equation 4.8 can be written as follows to convert it to a linear differential equation.
- The above formula is the differential equation for R, and the solution of the linear differential equation is
- Approximate solution using Taylor series
- Linear differential equation solution
- 국부 미분 관계 Local differential relationship
Definition of Lie Algebra
- Each Lie group has a corresponding Lie Algebra
- Lie Algebra is a local property of Lie Group
- Lie algebra consists of a vector space V, a real set F, and a two-term operation[,].
- Element notation of SO(3): (1) 3D vector and (2) 3x3 matrix can be expressed. The meanings of the two are the same, and ^ and v can be used to convert and notify matrix to vector using vector to matrix.
- Element notation of SE(3) :(1)6 dimensional vector and (2)4x4 matrix can be expressed Translation and rotatio can be expressed as rho and phi The meaning of the two is the same, and using ^ and v to matrix from vector to matrix From vector to vector and notation
<a href=https://postimg.cc/G490Jw8M”>
Reference
SLAM KR

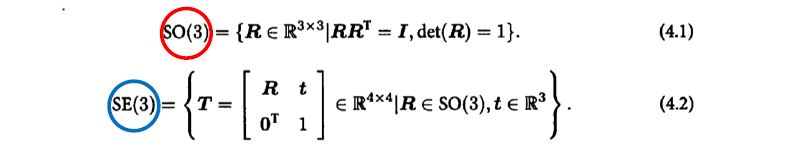
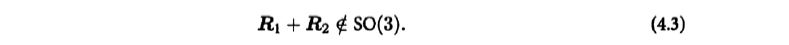
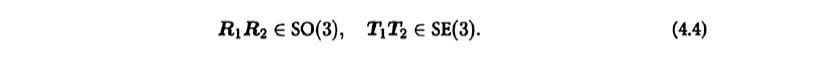

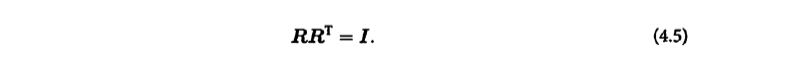
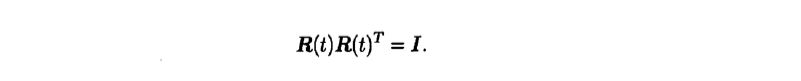




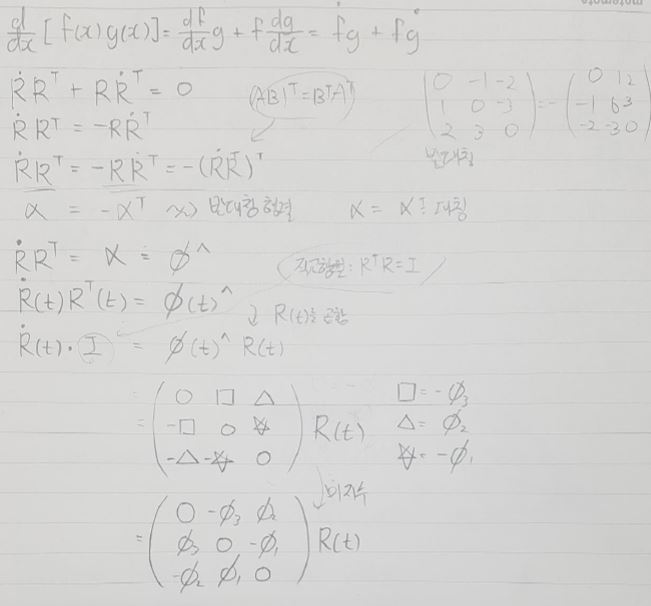

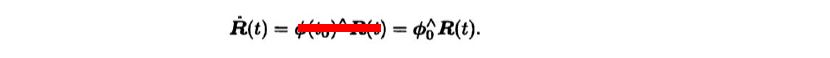
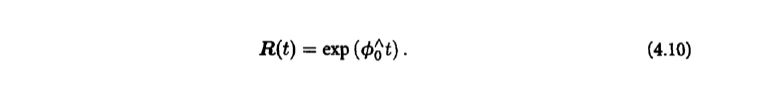

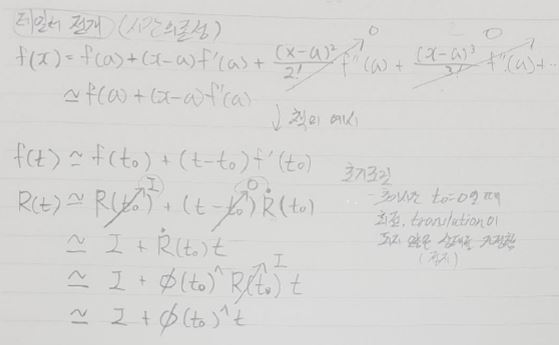




Comments