10. State Estimation.
17 Jun 2020 | Visual SLAM
Introduction
- Understanding equations for state estimation
- Understanding state estimation methodologies
- Incremental / filter technique
- 일괄 처리 (Batch)
- Understanding the mathematical techniques used in batch state estimation
- Maximum A Posteriori (MAP)
- Maximum Likelihood (MLE)
State estimation Method
- 운동 방정식 = 내부 센서를 통해 추정한 위치 (e.g. wheel odometry)
- Equation of motion = position estimated by an internal sensor (e.g. wheel odometry)
- 관측 방정식 = 외부 센서를 통해 추정한 위치 (e.g. 카메라, gps)
- Observation equation = position estimated by external sensor (e.g. camera, gps)
Observation equation by Camera
- When using a camera, the observation equation can be converted as shown on the above.
state estimation methodologies
- Incremental / filter technique
- predict a post pose based on the current poise when updating data at a new pose
- Extended Kalman Filter
- Batch
- Process all input/observed data from 0 to k points at once to accurately map positions from 0 to k
- Loop Closure
- Structure From Motion(SfM)
Probabilistic representation of state estimation
- Considering every moment from 1 to N and assuming there are M landmarks
- Maximizing the posterior is called Maximum a posteriori (MAP). For MAP, the denominator(분모) is not related to the estimated state x,y, so the denominator is removed.
- The objective is to maximize Likelihood and Prior to obtain the maximum Posterior. However, currently we don’t know where the robot pose or landmark is, so there is no prior, so we have to solve the Maximum Likelihood Estimation (MLE).
-
위의 식을 직관적으로 풀면 ‘현재 위치에서 어떤 관측지가 만들어질지'에 대한 확률을 풀어내는 것.
-
To find the maximum likelihood for an observation, we need to find the conditional probability of the observed data. The noise of the observation model is expressed as follows because it follows the Gaussian distribution expressed in the previous explanation.
- In general, the control inputs and observations of each frame are independent of each other.
- Therefore, motion and observation are processed independently, and there is an independent error between each model.
Reference
SLAM KR
Introduction
- Understanding equations for state estimation
- Understanding state estimation methodologies
- Incremental / filter technique
- 일괄 처리 (Batch)
- Understanding the mathematical techniques used in batch state estimation
- Maximum A Posteriori (MAP)
- Maximum Likelihood (MLE)
State estimation Method
- 운동 방정식 = 내부 센서를 통해 추정한 위치 (e.g. wheel odometry)
- Equation of motion = position estimated by an internal sensor (e.g. wheel odometry)
- 관측 방정식 = 외부 센서를 통해 추정한 위치 (e.g. 카메라, gps)
- Observation equation = position estimated by external sensor (e.g. camera, gps)
Observation equation by Camera
- When using a camera, the observation equation can be converted as shown on the above.
state estimation methodologies
- Incremental / filter technique
- predict a post pose based on the current poise when updating data at a new pose
- Extended Kalman Filter
- Batch
- Process all input/observed data from 0 to k points at once to accurately map positions from 0 to k
- Loop Closure
- Structure From Motion(SfM)
Probabilistic representation of state estimation
- Considering every moment from 1 to N and assuming there are M landmarks
- Maximizing the posterior is called Maximum a posteriori (MAP). For MAP, the denominator(분모) is not related to the estimated state x,y, so the denominator is removed.
- The objective is to maximize Likelihood and Prior to obtain the maximum Posterior. However, currently we don’t know where the robot pose or landmark is, so there is no prior, so we have to solve the Maximum Likelihood Estimation (MLE).
-
위의 식을 직관적으로 풀면 ‘현재 위치에서 어떤 관측지가 만들어질지'에 대한 확률을 풀어내는 것.
-
To find the maximum likelihood for an observation, we need to find the conditional probability of the observed data. The noise of the observation model is expressed as follows because it follows the Gaussian distribution expressed in the previous explanation.
- In general, the control inputs and observations of each frame are independent of each other.
- Therefore, motion and observation are processed independently, and there is an independent error between each model.
Reference
SLAM KR

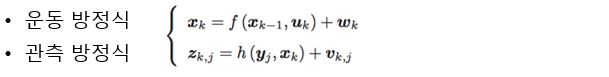

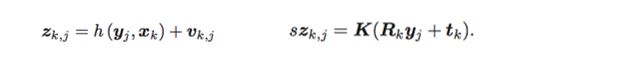

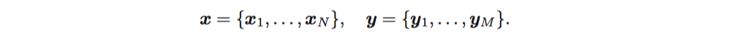

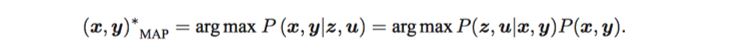
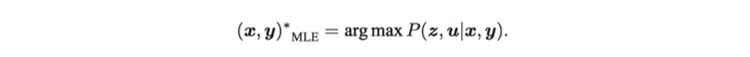
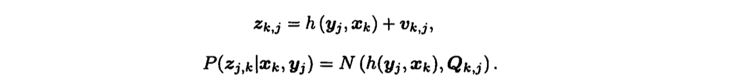


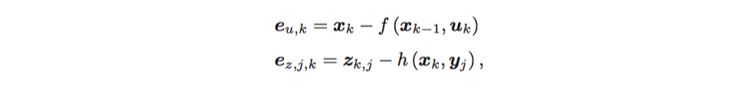

Comments