13. Visual odometer(3D-2D Matching(3D-2D로 자세 추정 방법))
18 Jun 2020 | Visual SLAM
Recap
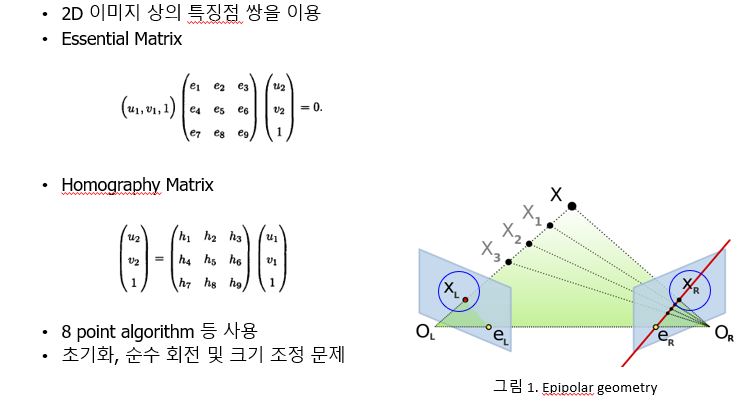
- 2D-2D: epipolar geometry
- Using a pair of feature points on a 2D image
Introduction
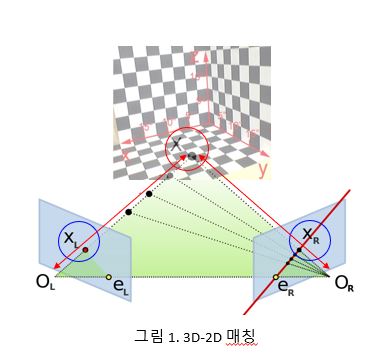
- 3D-2D Matching : PnP(Perspective-n-Point)
- estimate the camera’s pose movement given the correspondence between 3D and 2D
- 3D: Camera coordinate system or world coordinate system
- 2D: Image coordinate system
- Used for RGB-D odometry, calibration, etc.
- Motion estimation without epipolar constraints is possible even in environments where the number of matching points is small.
- Method(linear, Non-linear):
- DLT(Direct Linear Transformation)
- P3P
- EPnP(Efficient PnP)
- UPnP
- Bundle Adjustment
Direct Linear Transform, DLT
- Linear change relational solution
- Each feature point provides two linear equations for t
- T has a total of 12 dimensions, so at least 6 pairs are required. (Actually 11, 5.5 pairs)
- Find the least squares solution for the over-determined equation using the method as SVD.
- Find the optimum value of R and t using methods such as QR decomposition
- Here, it is assumed that it is calibrated, so internal parameters are not considered.
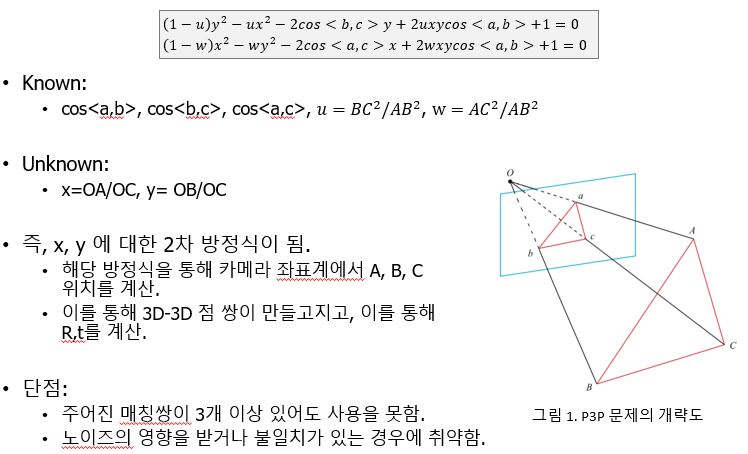
P3P
- Solve problems using only 3 pairs of match points.
- Using a triangular match (shares the angle of incidence for the camera optical center O).
- The location of A, B, and C in the world coordinate system, not the camera coordinate system.
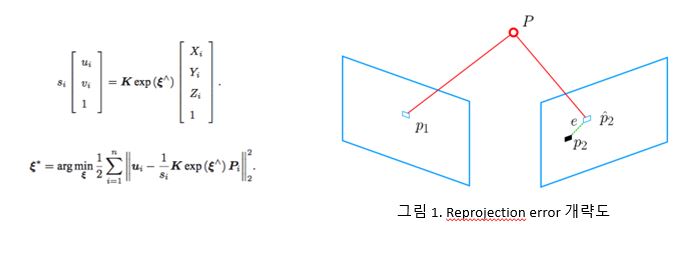
Bundle Adjustment
- Bundle: A bundle of multiple light rays
- solve the nonlinear least squares problem
- Linear Method: Often find the camera posture first, then the location of the space(Cloused-form solution)
- Nonlinear method: Optimize the camera posture and spatial point position together by considering them as optimization variables. (Non-linear optimization, iterative solution)
- Bundle adjustment in PnP minimizes reprojection errors.
- R, t calculation using Lie algebra
Reference
SLAM KR
Recap
- 2D-2D: epipolar geometry
- Using a pair of feature points on a 2D image
Introduction
- 3D-2D Matching : PnP(Perspective-n-Point)
- estimate the camera’s pose movement given the correspondence between 3D and 2D
- 3D: Camera coordinate system or world coordinate system
- 2D: Image coordinate system
- Used for RGB-D odometry, calibration, etc.
- Motion estimation without epipolar constraints is possible even in environments where the number of matching points is small.
- Method(linear, Non-linear):
- DLT(Direct Linear Transformation)
- P3P
- EPnP(Efficient PnP)
- UPnP
- Bundle Adjustment
Direct Linear Transform, DLT
- Linear change relational solution
- Each feature point provides two linear equations for t
- T has a total of 12 dimensions, so at least 6 pairs are required. (Actually 11, 5.5 pairs)
- Find the least squares solution for the over-determined equation using the method as SVD.
- Find the optimum value of R and t using methods such as QR decomposition
- Here, it is assumed that it is calibrated, so internal parameters are not considered.
P3P
- Solve problems using only 3 pairs of match points.
- Using a triangular match (shares the angle of incidence for the camera optical center O).
- The location of A, B, and C in the world coordinate system, not the camera coordinate system.
Bundle Adjustment
- Bundle: A bundle of multiple light rays
- solve the nonlinear least squares problem
- Linear Method: Often find the camera posture first, then the location of the space(Cloused-form solution)
- Nonlinear method: Optimize the camera posture and spatial point position together by considering them as optimization variables. (Non-linear optimization, iterative solution)
- Bundle adjustment in PnP minimizes reprojection errors.
- R, t calculation using Lie algebra
Reference
SLAM KR





Comments