15. Visual odometer(Direct Method)
21 Jun 2020 | Visual SLAM
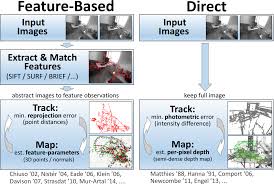
Introduction
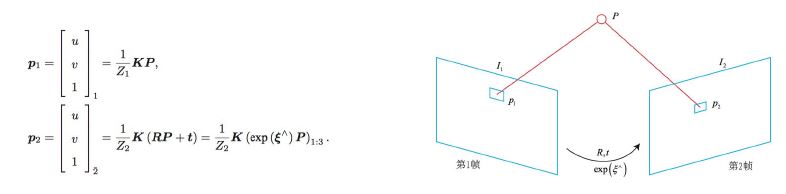
- World coordinates of space point P are [X, Y, Z], non-homogeneous pixel coordinates are p1, p2
- Find the relative pose transformation of the second camera relative to the first camera
- The internal parameter K is the same
- There is no way to know which p2 corresponds to the same point as p1 (feature matching X)
- Find the location of p2 based on the current pose estimate
- Optimize camera poses to make p2 and p1 similar
- Z는 Depth, 이 방법은 Gray scale을 사용하여 찾는 방법(Feature point방법이 아님)
Direct Method Process
- Optimization problem → Minimize photometric error(측광오차)
- The optimization goal is L2 norm of error
- Assumptions: Gray scale is immutable
- The overall camera pose estimation problem for multiple points is as follows (camera pose ξ optimization)
- How does the error e change with the camera pose? → differential
- Using perturbation models for Lie algebra
- Jacobian Matrix Derivation of Error for Lie Algebra
- Calculate Jacobian of the optimization problem using the above method for the problem of N points
- Use G-N (Gauss-Newton) or L-M (Levenberg-Marquardt)
Discuss
- P is a spatial point at a known location, monocular cameras are more difficult (uncertainty caused by the depth of P)
- Classification based on the source of P
- Sparse Features
- Hundreds to thousands of specific points. No need to calculate descriptors, only use hundreds of pixels(feature point by feature-based or direct method), so it’s the fastest but only sparse reconstruction
- Partial pixel
- In equation (8.16), when the pixel gradient is 0, the total Jacobian is 0 and does not contribute to the motion increment calculation. Therefore, use only pixels with gradients, ignoring areas where the gradients are not clear. Semi-dense direct method
- All pixels
- Dense Direct Method. Most cannot be computed in real time on existing CPUs and require GPUs. The fact that the gradient is unclear does not contribute much to motion estimation and it is difficult to predict the position during reconstruction.
Exercise
- Direct method relies entirely on optimization to solve camera poses
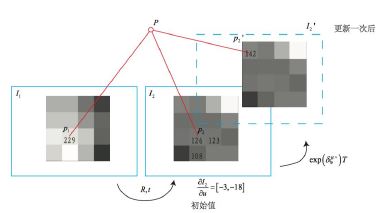
- Measure pixels with gray value 229, location of spatial point P in world coordinates
- You need to get a new image for the next timestamp and estimate the camera pose at this location → iteratively optimize the initial value
- At this initial value, the gray scale value of the pixel after projection of the spatial point P is 126, and the error is 229-126 = 103
- Fine-tune the pose of the camera to reduce errors, making pixels brighter
- To know the fine adjustment value of the camera pose, we need the surrounding pixel gradient.
- The gradient around the pixel is [-3, -18].
- To improve brightness, use an optimization algorithm that fine-tunes the camera so that the image in P moves to the top left
- After referring to the values of many pixels, the optimization algorithm selects a place not far from the direction we proposed and calculates the exp( ξ^) of the update quantity.
Direct Method Pros Vs Cons
- Pros
- Feature point, descriptor calculation time omitted
- Can be used when feature point matching is difficult (pixel gradient only)
- Semi-Dense or Dense Mapping available
- Cons
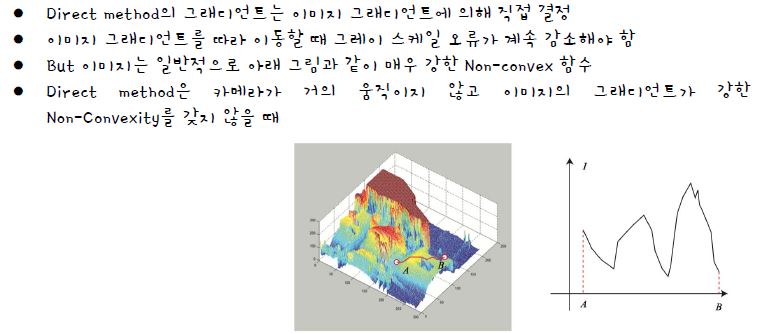
- entirely dependent on gradient
- But, the image is a strong non-convex function
- Optimization algorithm easily falls into local minima, succeeds only when motion is small
- Strong assumption that grayscale values are immutable
- Automatic exposure compensation for the camera
- Lighting change
- Camera calibration using photometric model (when exposure time is changed)
Reference
SLAM KR
Introduction
- World coordinates of space point P are [X, Y, Z], non-homogeneous pixel coordinates are p1, p2
- Find the relative pose transformation of the second camera relative to the first camera
- The internal parameter K is the same
- There is no way to know which p2 corresponds to the same point as p1 (feature matching X)
- Find the location of p2 based on the current pose estimate
- Optimize camera poses to make p2 and p1 similar
- Z는 Depth, 이 방법은 Gray scale을 사용하여 찾는 방법(Feature point방법이 아님)
Direct Method Process
- Optimization problem → Minimize photometric error(측광오차)
- The optimization goal is L2 norm of error
- Assumptions: Gray scale is immutable
- The overall camera pose estimation problem for multiple points is as follows (camera pose ξ optimization)
- How does the error e change with the camera pose? → differential
- Using perturbation models for Lie algebra
- Jacobian Matrix Derivation of Error for Lie Algebra
- Calculate Jacobian of the optimization problem using the above method for the problem of N points
- Use G-N (Gauss-Newton) or L-M (Levenberg-Marquardt)
Discuss
- P is a spatial point at a known location, monocular cameras are more difficult (uncertainty caused by the depth of P)
- Classification based on the source of P
- Sparse Features
- Hundreds to thousands of specific points. No need to calculate descriptors, only use hundreds of pixels(feature point by feature-based or direct method), so it’s the fastest but only sparse reconstruction
- Partial pixel
- In equation (8.16), when the pixel gradient is 0, the total Jacobian is 0 and does not contribute to the motion increment calculation. Therefore, use only pixels with gradients, ignoring areas where the gradients are not clear. Semi-dense direct method
- All pixels
- Dense Direct Method. Most cannot be computed in real time on existing CPUs and require GPUs. The fact that the gradient is unclear does not contribute much to motion estimation and it is difficult to predict the position during reconstruction.
Exercise
- Direct method relies entirely on optimization to solve camera poses
- Measure pixels with gray value 229, location of spatial point P in world coordinates
- You need to get a new image for the next timestamp and estimate the camera pose at this location → iteratively optimize the initial value
- At this initial value, the gray scale value of the pixel after projection of the spatial point P is 126, and the error is 229-126 = 103
- Fine-tune the pose of the camera to reduce errors, making pixels brighter
- To know the fine adjustment value of the camera pose, we need the surrounding pixel gradient.
- The gradient around the pixel is [-3, -18].
- To improve brightness, use an optimization algorithm that fine-tunes the camera so that the image in P moves to the top left
- After referring to the values of many pixels, the optimization algorithm selects a place not far from the direction we proposed and calculates the exp( ξ^) of the update quantity.
Direct Method Pros Vs Cons
- Pros
- Feature point, descriptor calculation time omitted
- Can be used when feature point matching is difficult (pixel gradient only)
- Semi-Dense or Dense Mapping available
- Cons
- entirely dependent on gradient
- But, the image is a strong non-convex function
- Optimization algorithm easily falls into local minima, succeeds only when motion is small
- Strong assumption that grayscale values are immutable
- Automatic exposure compensation for the camera
- Lighting change
- Camera calibration using photometric model (when exposure time is changed)
- entirely dependent on gradient
Reference
SLAM KR

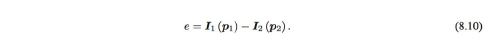
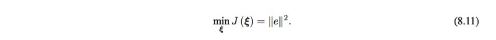



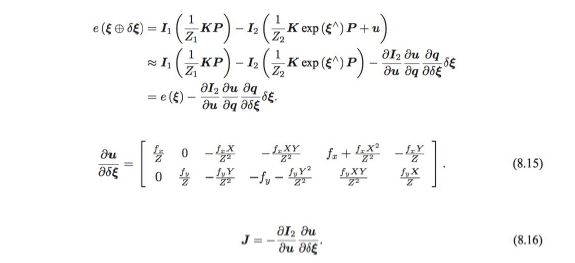

Comments