19. Backend 2
22 Jun 2020 | Visual SLAM
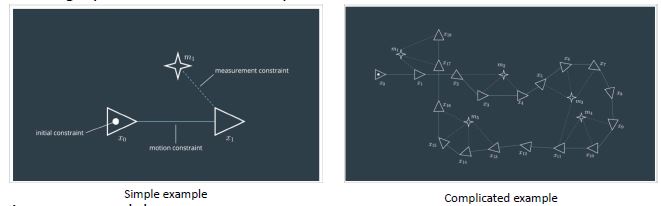
Graph SLAM
- Graph-based formulation of the SLAM problem by Lu and Milios in 1997
- Build the graph and find the robot poses and landmarks that minimize the error
- Spring-mass model
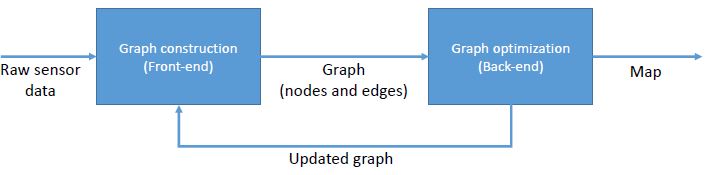
Front-end and Back-end
- Front-end
- construct the graph using the odometry and sensory measurements by the robot
- Data association
- 즉 Feature Based로 구해진 MapPoint 및 키프레임 포즈 든, Direct Method로 Intensity를 통해 구해진 MapPoint 및 키프레임 포즈든, 키 데이터들을 데이터 베이스에다가 저장 하여 Covisibility 등을 생성
- Back-end
- input
- The completed graph with all of the constraints
- 데이터 베이스에 Covisibility를 Essential Graph로 최적화 시기거나 BA방법 등을 사용하여서 Camera Pose 와 MapPoint 교정
- Output
- The most probable configuration of robot poses and map features
- 현재 프레임에서 얻어지는 Camera Pose와 MapPoints의 Pose를 얻을 수 있음
- Graph optimization
- Find the system configuration that produces the smallest error
- 데이터 베이스에 저장된 데이터들을 가지고 최적화
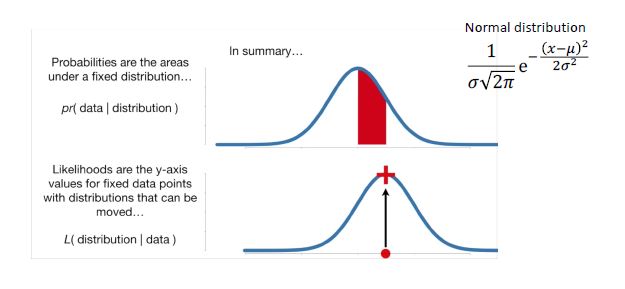
Maximum Likelihood Estimation
- Probability
- The ratio at which the observed value will appear in a given probability distribution.
- Likelihood
- Concept complementary to probability
- The ratio at which a given observation will yield this probability distribution
- 즉 확률 분포를 움직여서 꼭대기 점을 얻는 파라미터
1-Dimensional Case
- Negative Log를 취해주면 Minimum 값을 구할 수 있다.
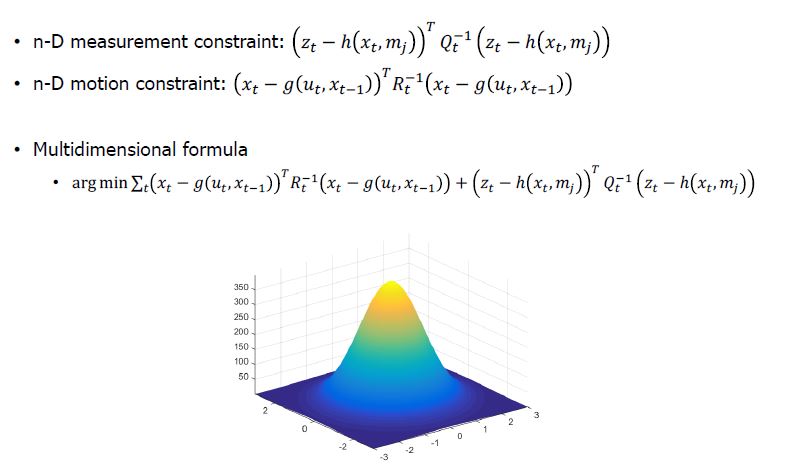
N-Dimensional Case
- Q is covariance of Measurement(Measurement noise), R is covariance of Motion Model(Process noise)
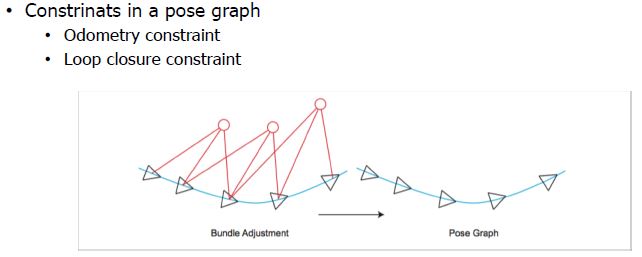
Pose Graph Optimization(PGO)
- 간혈적으로 랜드마크를 사용
- Disadvantages of bundle adjustment, graph slam
- Over time, the trajectory of the robot increases and the map continues to grow in size.
- As the size of the map grows, the number of constraints to be calculated increases exponentially.
- Can I ignore the landmark(MapPoints) when to perform optimization?
- Graph optimization considering only robot pose
- When the initial estimation of the robot pose using the landmark is completed, the location of the landmark is no longer optimized, and only the connection between the camera poses is optimized.
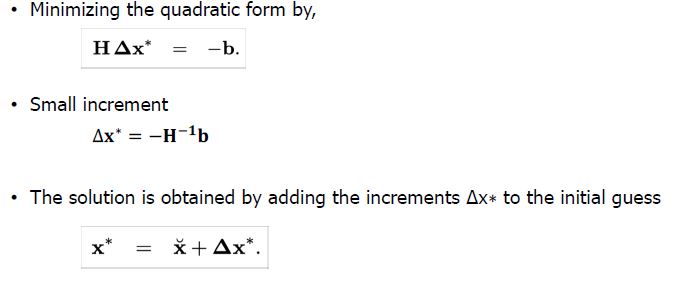
Least Squares Optimization
Structure of Linearized System
Pseudo Code
PGO on a Manifold
- Overall objective function form (least squares)
- T는 R,T 행렬로 (4x4)
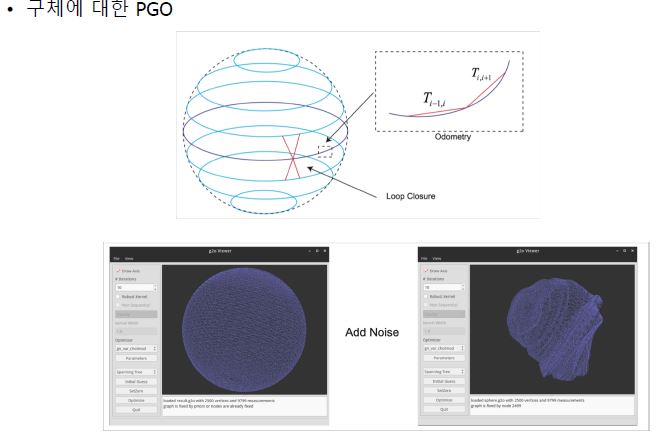
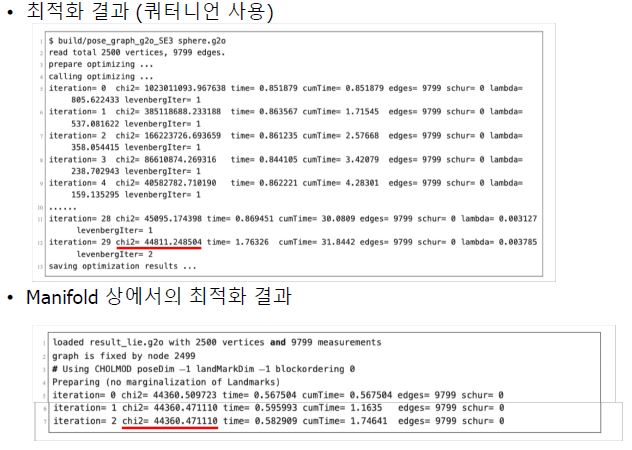
Experiment
- 빨간 부분은 에러값
Reference
SLAM KR
Graph SLAM
- Graph-based formulation of the SLAM problem by Lu and Milios in 1997
- Build the graph and find the robot poses and landmarks that minimize the error
- Spring-mass model
Front-end and Back-end
- Front-end
- construct the graph using the odometry and sensory measurements by the robot
- Data association
- 즉 Feature Based로 구해진 MapPoint 및 키프레임 포즈 든, Direct Method로 Intensity를 통해 구해진 MapPoint 및 키프레임 포즈든, 키 데이터들을 데이터 베이스에다가 저장 하여 Covisibility 등을 생성
- Back-end
- input
- The completed graph with all of the constraints
- 데이터 베이스에 Covisibility를 Essential Graph로 최적화 시기거나 BA방법 등을 사용하여서 Camera Pose 와 MapPoint 교정
- The completed graph with all of the constraints
- Output
- The most probable configuration of robot poses and map features
- 현재 프레임에서 얻어지는 Camera Pose와 MapPoints의 Pose를 얻을 수 있음
- The most probable configuration of robot poses and map features
- Graph optimization
- Find the system configuration that produces the smallest error
- 데이터 베이스에 저장된 데이터들을 가지고 최적화
- input
Maximum Likelihood Estimation
- Probability
- The ratio at which the observed value will appear in a given probability distribution.
- Likelihood
- Concept complementary to probability
- The ratio at which a given observation will yield this probability distribution
- 즉 확률 분포를 움직여서 꼭대기 점을 얻는 파라미터
1-Dimensional Case
- Negative Log를 취해주면 Minimum 값을 구할 수 있다.
N-Dimensional Case
- Q is covariance of Measurement(Measurement noise), R is covariance of Motion Model(Process noise)
Pose Graph Optimization(PGO)
- 간혈적으로 랜드마크를 사용
- Disadvantages of bundle adjustment, graph slam
- Over time, the trajectory of the robot increases and the map continues to grow in size.
- As the size of the map grows, the number of constraints to be calculated increases exponentially.
- Can I ignore the landmark(MapPoints) when to perform optimization?
- Graph optimization considering only robot pose
- When the initial estimation of the robot pose using the landmark is completed, the location of the landmark is no longer optimized, and only the connection between the camera poses is optimized.
Least Squares Optimization
Structure of Linearized System
Pseudo Code
PGO on a Manifold
- Overall objective function form (least squares)
- T는 R,T 행렬로 (4x4)
Experiment
- 빨간 부분은 에러값
Reference
SLAM KR







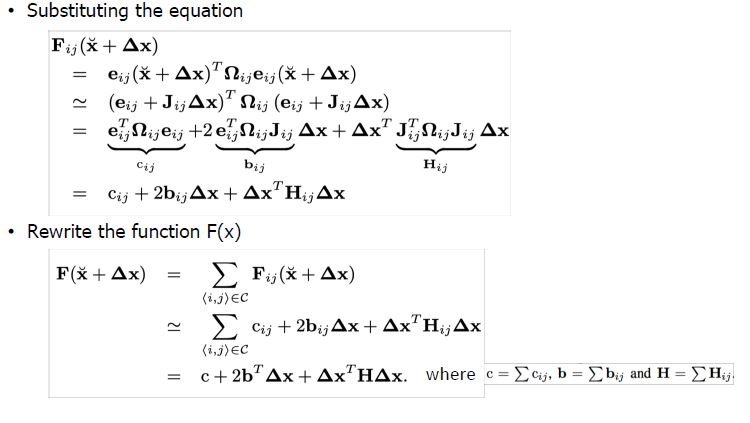




Comments