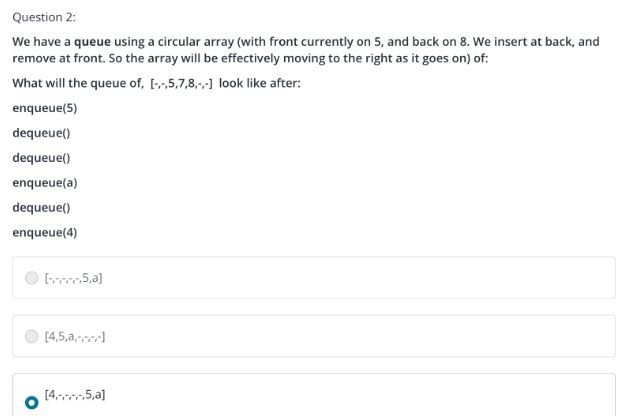
11.selection Sort
11 May 2020 | Data structure_1
Introduction
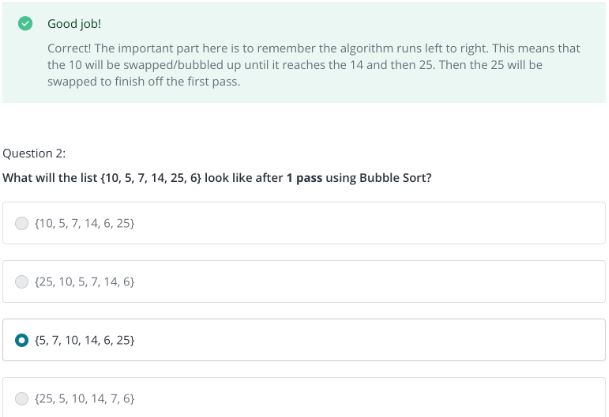
- The selection sort is very similar to that of bubble sort. Instead of finding a max however, It repeatedly finds the minimum element from the unsorted portion, and puts it into a “sorted portion”
Why is it Important?
- Selection sort is the next logical step from bubble sort. It does what bubble sort does, but has one large difference. Instead of searching through the entire array each time, it creates and only searches an “unsorted portion”.
Lesson Notes
- The algorithm works by creating two subarrays within an array. The first subarray is the portion that is already sorted. The second is everything that is unsorted. Typically this is kept track of with an index number. So if our index number was 3, then everything to the right of and equal to 3, is the current sorted portion.
-
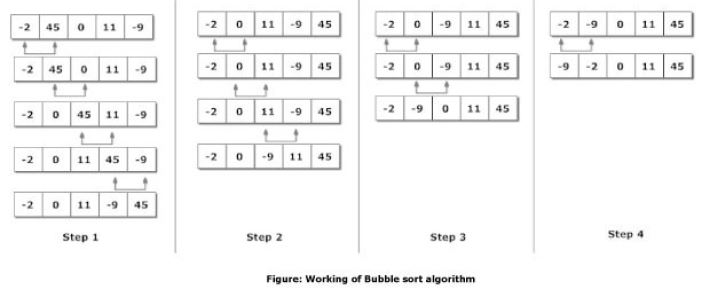
As you can see in the figure above, with each operation, the sorted portion grows and the unsorted portion shrinks. The algorithm works by finding the minimum number, then swapping it with the array index closest to the sorted portion.
-
For example, in the first example, 8 is the number that will be swapped. This is because the sorted portion doesn’t exist yet, so the 8 is the closest to the left. We then go through the array and find the minimum value, which in this case is 1. We swap 8 and 1 and do it again.
-
The 1 is now in the sorted portion. We move to the closest value to the sorted portion (So one to the right of the boundry of the sorted portion) which is the 5. We then look for the smallest number in the unsorted portion. We find the 3, and swap the 5 and 3. Now the sorted portion is two big. We continue this process until the entire array is sorted
-
This although slightly faster than bubble sort, doesn’t improve the run time by any large magnitude. It still is on average a runtime of n^2. You can see the math for this under the diagram. It is still making n(n-1)/2 comparisons. This reduces to (n^2-n)/2 operations. Remember when we go to infinity we grab the largest magnitude. So in this case, the n^2 is the
only thing that stays.
-
Best Time: Ω(n^2) : Even if the array is already sorted, selection sort must run through its entire algorithm to figure this out. This means it will generate an already sorted portion, and only increase it by 1 on each operation. So the total run time will still come out to be n^2
-
Average Time: Θ(n^2) : Same with the average time. It doesn’t matter how unsorted or sorted the array is, it will run through all operations each time. Although the magnitudes of this and bubble sort are the same, this one is technically faster because it reduces the size of the search area each time, unlike bubble sort which searches the entire array each time.
-
Worst Time: O(n^2) : Same with the worst-case time. It will use the same operations no matter how sorted or unsorted the array is. No one case is better or worse for selection sort.
Quiz
Introduction
- The selection sort is very similar to that of bubble sort. Instead of finding a max however, It repeatedly finds the minimum element from the unsorted portion, and puts it into a “sorted portion”
Why is it Important?
- Selection sort is the next logical step from bubble sort. It does what bubble sort does, but has one large difference. Instead of searching through the entire array each time, it creates and only searches an “unsorted portion”.
Lesson Notes
- The algorithm works by creating two subarrays within an array. The first subarray is the portion that is already sorted. The second is everything that is unsorted. Typically this is kept track of with an index number. So if our index number was 3, then everything to the right of and equal to 3, is the current sorted portion.
-
As you can see in the figure above, with each operation, the sorted portion grows and the unsorted portion shrinks. The algorithm works by finding the minimum number, then swapping it with the array index closest to the sorted portion.
-
For example, in the first example, 8 is the number that will be swapped. This is because the sorted portion doesn’t exist yet, so the 8 is the closest to the left. We then go through the array and find the minimum value, which in this case is 1. We swap 8 and 1 and do it again.
-
The 1 is now in the sorted portion. We move to the closest value to the sorted portion (So one to the right of the boundry of the sorted portion) which is the 5. We then look for the smallest number in the unsorted portion. We find the 3, and swap the 5 and 3. Now the sorted portion is two big. We continue this process until the entire array is sorted
-
This although slightly faster than bubble sort, doesn’t improve the run time by any large magnitude. It still is on average a runtime of n^2. You can see the math for this under the diagram. It is still making n(n-1)/2 comparisons. This reduces to (n^2-n)/2 operations. Remember when we go to infinity we grab the largest magnitude. So in this case, the n^2 is the only thing that stays.
-
Best Time: Ω(n^2) : Even if the array is already sorted, selection sort must run through its entire algorithm to figure this out. This means it will generate an already sorted portion, and only increase it by 1 on each operation. So the total run time will still come out to be n^2
-
Average Time: Θ(n^2) : Same with the average time. It doesn’t matter how unsorted or sorted the array is, it will run through all operations each time. Although the magnitudes of this and bubble sort are the same, this one is technically faster because it reduces the size of the search area each time, unlike bubble sort which searches the entire array each time.
-
Worst Time: O(n^2) : Same with the worst-case time. It will use the same operations no matter how sorted or unsorted the array is. No one case is better or worse for selection sort.