3.N-Notation
03 May 2020 | Data structure_1
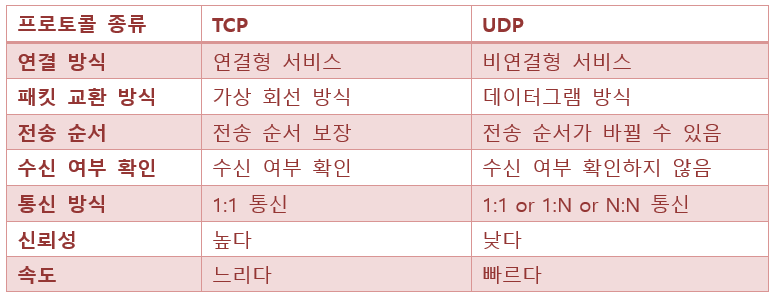
Introduction
- In computer science we need a way to be able to compare different algorithms with each other. We typically use the n-Notation for this.
Why is it Important?
- Run times of different programs are usually written in n-Notation. So if we want to look up how fast a certain algorithm is, we will need to know this notation to be able to understand it.
Lesson Notes
-
N-Notation is represented as a function of n. This simply means that the program is going to be related to the variable n in some way.
-
N-notation is NOT an analysis of how long an algorithm will take to run, but an analysis of how the algorithm will scale with more and more input data.
-
This method is based off looking at the input of the algorithm and analyzing how the algorithm works with this input. However, we don’t particularly know how many pieces of data will come in at any given moment. What we do is replace this input number with a variable, n.
-
For example, let’s say we have an algorithm which runs through the amount of Facebook friends you have. When we are writing the algorithm, we have no clue how many friends are going to be added as input. You could have 250, or 2,000, or 2. So instead of giving an actual number, we just say n pieces of data will be put into this algorithm
-
(The n here is just a variable, it could be x, or w, or z, but we typically use n). It is usually a count of how many operations are being run by a program. This can be the amount of inputs, the calculations, or the outputs
-
The reason we use n is because it will show us how our program might react differently to different amounts of data. We as computer scientists never know how many pieces of data our programs are going to handle. So instead, we look at how our program is going to grow with different amounts of inputs.
-
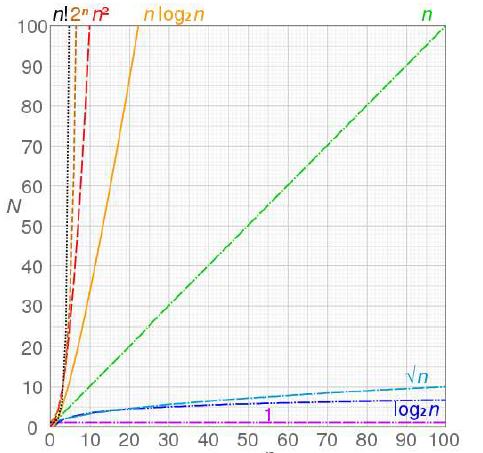
As you can see with this chart, the different values yield vastly different results. The difference between n and n^2 is substantial. If you brought this out to infinity, the difference would almost be a 90-degree angle. (As the difference between them would grow to nearly infinity)
-
We can use these different values to compare how our different algorithms might react to different amounts of data.
-
The above table represents the change. It inputs some different numbers as n and then displays what different n values would give. These numbers vary a lot with the given n-formulas.
-
For example, with only 1,000 pieces of data, the difference between n^2 and nlog(n) is from 1,000,000 to 9965. Even though they look decently close on the line-chart above, nlog(n) will only take 1% of the time as n^2. This difference will grow the larger our n becomes.
-
This is the key concept behind n-notation. Even though we don’t know the specific amount of data that is coming through our program, we can atleast compare it to another that accomplishes the same task. If one runs at n^2 while the other runs at n, we know the n will be faster in every case.
BIG O
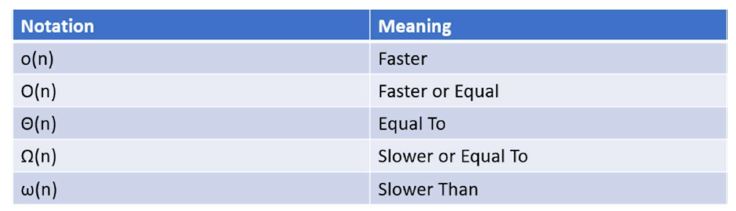
- We usually don’t use n by itself however. Typically we tie it together with a Greek letter to give it some context. Rarely does our program operate at the same timing for every single step. So instead of having exact values for things, we want to look at them in boundaries, or cases in which they are greater, less than, or equal.
-
For this notation, we just use one of the Greek symbols above, with our n notation inside of the parenthesis. So for example, O(nlogn) would mean that the program is faster or equal to nlogn.
-
The most important notation above is the Omicron, or “Big O”. The reason for this is because it gives us a worse case scenario. That means we know the absolute worse case scenario of our program, meaning if we plan for this, we won’t have any surprises or weird corner cases that come up.
-
We can then compare the worst case scenarios of programs to see which are faster. Since this is the absolute slowest the program can run, we know that one program will always run slower than another program!
-
For example let’s say that we have two programs, program A which runs at Ω(n) and program B which runs at Ω(n^2). Which of these two programs is better? Well all we know is that program A is slower or equal to n and program B is slower or equal to n^2. However that doesn’t guarantee anything. Program A could end up running around n^3 or n! and meet the requirements of Ω(n). B could do the exact same thing, so their speed is still arbitrary. So with these symbols, we don’t learn too much about the two programs.
-
However, if we used O(n) for A and O(n^2) for B, we can now compare the two. We know without a doubt that A will not run slower than n while B can run up to n^2. Therefore the faster is Program A, because it can never get slower than B
-
Let’s use some numbers to drive this point home a little more.
-
Let’s say we have a time scale to determine how fast our algorithm runs. In this scale the closer to 0 we go, the faster our algorithm. We can use to show why Big O is typically the most useful of these notations.
Notation of other comparison
-
ω(7) - The algorithm will run slower, or > 7. How much greater? 1,000. 1,000,000? There is no way to know. This algorithm could take years to complete the simplest of tasks.
-
Ω(7) - The algorithm will run “slower or equal” to 7, or >=7. Still could run in to infinity or really large run times
-
Θ(7) - The algorithm is equal to 7, or = 7. This would be great. If we can guarantee an algorithm will always run equal to something we would use this. However, this is highly unlikely in the real world, so it’s not used too often.
-
O(7) - The algorithm will run “faster or equal” to 7, or <=7. This is good. We have a limit on the algorithm. We know in all cases, 7 is the worst this algorithm can do. This can be used to plan with. No surprises will come up here.
-
o(7) - The algorithm will run faster than 7, or < 7. There is nothing inherently wrong with this, except that it’s just less accurate than O(7). How much faster will it run? 6? 2?. We don’t know the limit. Although we can still plan a worst case scenario with this, it’s less accurate than O(7) which is why it’s rarely used.
-
There you have it, BIg O notation. This is used all across computer science, and now you know how to read it!
Introduction
- In computer science we need a way to be able to compare different algorithms with each other. We typically use the n-Notation for this.
Why is it Important?
- Run times of different programs are usually written in n-Notation. So if we want to look up how fast a certain algorithm is, we will need to know this notation to be able to understand it.
Lesson Notes
-
N-Notation is represented as a function of n. This simply means that the program is going to be related to the variable n in some way.
-
N-notation is NOT an analysis of how long an algorithm will take to run, but an analysis of how the algorithm will scale with more and more input data.
-
This method is based off looking at the input of the algorithm and analyzing how the algorithm works with this input. However, we don’t particularly know how many pieces of data will come in at any given moment. What we do is replace this input number with a variable, n.
-
For example, let’s say we have an algorithm which runs through the amount of Facebook friends you have. When we are writing the algorithm, we have no clue how many friends are going to be added as input. You could have 250, or 2,000, or 2. So instead of giving an actual number, we just say n pieces of data will be put into this algorithm
-
(The n here is just a variable, it could be x, or w, or z, but we typically use n). It is usually a count of how many operations are being run by a program. This can be the amount of inputs, the calculations, or the outputs
-
The reason we use n is because it will show us how our program might react differently to different amounts of data. We as computer scientists never know how many pieces of data our programs are going to handle. So instead, we look at how our program is going to grow with different amounts of inputs.
-
As you can see with this chart, the different values yield vastly different results. The difference between n and n^2 is substantial. If you brought this out to infinity, the difference would almost be a 90-degree angle. (As the difference between them would grow to nearly infinity)
-
We can use these different values to compare how our different algorithms might react to different amounts of data.
-
The above table represents the change. It inputs some different numbers as n and then displays what different n values would give. These numbers vary a lot with the given n-formulas.
-
For example, with only 1,000 pieces of data, the difference between n^2 and nlog(n) is from 1,000,000 to 9965. Even though they look decently close on the line-chart above, nlog(n) will only take 1% of the time as n^2. This difference will grow the larger our n becomes.
-
This is the key concept behind n-notation. Even though we don’t know the specific amount of data that is coming through our program, we can atleast compare it to another that accomplishes the same task. If one runs at n^2 while the other runs at n, we know the n will be faster in every case.
BIG O
- We usually don’t use n by itself however. Typically we tie it together with a Greek letter to give it some context. Rarely does our program operate at the same timing for every single step. So instead of having exact values for things, we want to look at them in boundaries, or cases in which they are greater, less than, or equal.
-
For this notation, we just use one of the Greek symbols above, with our n notation inside of the parenthesis. So for example, O(nlogn) would mean that the program is faster or equal to nlogn.
-
The most important notation above is the Omicron, or “Big O”. The reason for this is because it gives us a worse case scenario. That means we know the absolute worse case scenario of our program, meaning if we plan for this, we won’t have any surprises or weird corner cases that come up.
-
We can then compare the worst case scenarios of programs to see which are faster. Since this is the absolute slowest the program can run, we know that one program will always run slower than another program!
-
For example let’s say that we have two programs, program A which runs at Ω(n) and program B which runs at Ω(n^2). Which of these two programs is better? Well all we know is that program A is slower or equal to n and program B is slower or equal to n^2. However that doesn’t guarantee anything. Program A could end up running around n^3 or n! and meet the requirements of Ω(n). B could do the exact same thing, so their speed is still arbitrary. So with these symbols, we don’t learn too much about the two programs.
-
However, if we used O(n) for A and O(n^2) for B, we can now compare the two. We know without a doubt that A will not run slower than n while B can run up to n^2. Therefore the faster is Program A, because it can never get slower than B
-
Let’s use some numbers to drive this point home a little more.
-
Let’s say we have a time scale to determine how fast our algorithm runs. In this scale the closer to 0 we go, the faster our algorithm. We can use to show why Big O is typically the most useful of these notations.
Notation of other comparison
-
ω(7) - The algorithm will run slower, or > 7. How much greater? 1,000. 1,000,000? There is no way to know. This algorithm could take years to complete the simplest of tasks.
-
Ω(7) - The algorithm will run “slower or equal” to 7, or >=7. Still could run in to infinity or really large run times
-
Θ(7) - The algorithm is equal to 7, or = 7. This would be great. If we can guarantee an algorithm will always run equal to something we would use this. However, this is highly unlikely in the real world, so it’s not used too often.
-
O(7) - The algorithm will run “faster or equal” to 7, or <=7. This is good. We have a limit on the algorithm. We know in all cases, 7 is the worst this algorithm can do. This can be used to plan with. No surprises will come up here.
-
o(7) - The algorithm will run faster than 7, or < 7. There is nothing inherently wrong with this, except that it’s just less accurate than O(7). How much faster will it run? 6? 2?. We don’t know the limit. Although we can still plan a worst case scenario with this, it’s less accurate than O(7) which is why it’s rarely used.
-
There you have it, BIg O notation. This is used all across computer science, and now you know how to read it!