30. Standard Template library(STL) - List, Stack & Queues, Complex Data
30 Sep 2019 | C++
List
- 리스트(list) 의 경우 양방향 연결 구조를 가진 자료형이라 볼 수 있습니다.
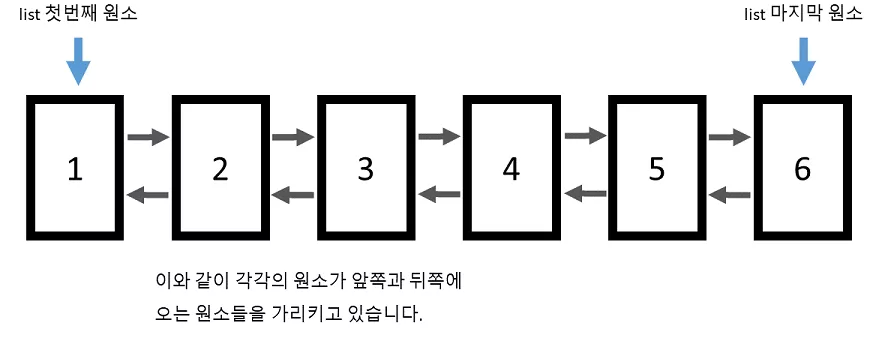
- 따라서 vector 와는 달리 임의의 위치에 있는 원소에 접근을 바로 할 수 없습니다.
- list 컨테이너 자체에서는 시작 원소와 마지막 원소의 위치만을 기억하기 때문에, 임의의 위치에 있는 원소에 접근하기 위해서는 하나씩 링크를 따라가야 합니다.
- 그래서 리스트에는 아예 [] 나 at 함수가 아예 정의되어 있지 않습니다.
- vector 의 경우 맨 뒤를 제외하고는 임의의 위치에 원소를 추가하거나 제거하는 작업이 O(n)O(n) 이였지만 리스트의 경우 O(1)O(1) 으로 매우 빠르게 수행될 수 있습니다.
- 왜냐하면 원하는 위치 앞과 뒤에 있는 링크값만 바꿔주면 되기 때문입니다.
예제
#include <iostream>
#include <list>
int main() {
std::list<int> lst;
lst.push_back(10);
lst.push_back(20);
lst.push_back(30);
lst.push_back(40);
for (std::list<int>::iterator itr = lst.begin(); itr != lst.end(); ++itr) {
std::cout << *itr << std::endl;
}
}
결과
10
20
30
40
- 주의할 점은 리스트의 반복자의 경우 다음과 같은 연산 밖에 수행 할 수 없습니다.
itr++ // itr ++
itr-- // --itr 도 됩니다.
itr + 5 //불가능
- 임의의 위치에 있는 원소를 가리킬 수 없다는 것입니다.
- 반복자는 오직 한 칸 씩 밖에 움직일 수 없습니다.
- 즉, 메모리 상에서 원소들이 연속적으로 존재하지 않을 수 있다는 뜻입니다.
- 반면에 벡터의 경우 메모리 상에서 연속적으로 존재하기 때문에 쉽게 임의의 위치에 있는 원소를 참조할 수 있습니다.
- erase 함수를 이용하여 원하는 위치에 있는 원소를 지울 수 도 있습니다.
- 리스트의 경우는 벡터와는 다르게, 원소를 지워도 반복자가 무효화 되지 않습니다.
- 왜냐하면, 각 원소들의 주소값들은 바뀌지 않기 때문입니다.
Example
- 1번째 배열에 100이 추가가 된다.
#include <iostream>
#include <list>
template <typename T>
void print_list(std::list<T>& lst) {
std::cout << "[ ";
// 전체 리스트를 출력하기 (이 역시 범위 기반 for 문을 쓸 수 있습니다)
for (const auto& elem : lst) {
std::cout << elem << " ";
}
std::cout << "]" << std::endl;
}
int main() {
std::list<int> lst;
lst.push_back(10);
lst.push_back(20);
lst.push_back(30);
lst.push_back(40);
std::cout << "처음 리스트의 상태 " << std::endl;
print_list(lst);
for (std::list<int>::iterator itr = lst.begin(); itr != lst.end(); ++itr) {
// 만일 현재 원소가 20 이라면
// 그 앞에 50 을 집어넣는다.
if (*itr == 20) {
lst.insert(itr, 50);
}
}
std::cout << "값이 20 인 원소 앞에 50 을 추가 " << std::endl;
print_list(lst);
for (std::list<int>::iterator itr = lst.begin(); itr != lst.end(); ++itr) {
// 값이 30 인 원소를 삭제한다.
if (*itr == 30) {
lst.erase(itr);
break;
}
}
std::cout << "값이 30 인 원소를 제거한다" << std::endl;
print_list(lst);
}
Result
처음 리스트의 상태
[ 10 20 30 40 ]
값이 20 인 원소 앞에 50 을 추가
[ 10 50 20 30 40 ]
값이 30 인 원소를 제거한다
[ 10 50 20 40 ]
Stack & Queues
- queue : 리스트 한쪽 끝에서만 삽입과 삭제가 일어나는 스택과 달리 리스트의 한쪽 끝에서는 원소들이 삭제되고 반대쪽 끝에서는 삽입만 가능하게 하는 순서화된 리스트 이다. 선입선출 리스트
- explicit Test(string name) : name(name)
- ex) float number = number1; <- 묵시적 형변환
- ex) float number = (int)number1; <- 명시적 형변환
#include <iostream>
#include <string>
#include <stack>
#include <queue>
using namespace std;
class Test
{
string name;
public:
explicit Test(string name) : name(name)
//묵시적인 타입변환을 하지 않고 명시적으로 타입변환을 하였을 경우에만 사용하겠다라는 뜻.
//ex) float number = number1; <- 묵시적 형변환
//ex) float number = (int)number1; <- 명시적 형변환
{
}
~Test()
{
}
void print() const
{
cout << name << endl;
}
};
int main(int argc, char const *argv[])
{
//LIFO(last in first out)
stack<Test> testStack;
testStack.push(Test("Mike"));
testStack.push(Test("John"));
testStack.push(Test("Sue"));
cout << endl;
/* this is invalid code ! objected destroyed.
Test &test1 = testStack.top();
testStock.pop();
test1.print(); // Reference refers to destroyed objects
*/
Test &test1 = testStack.top();
// reference.
test1.print();
// but original gone but test still have value
// this is last one
// .pop is the return the original.
// pop is object destroyed.(top 에 있는 원소를 삭제)
testStack.pop();
Test &test2 = testStack.top();
test2.print();
// the result is john.
//FIFO(first in first out) stack 이랑 반대라 생각하면 된다.
queue<Test> testQueue;
testQueue.push(Test("Mike"));
testQueue.push(Test("John"));
testQueue.push(Test("Sue"));
//여기서는 슈가 마지막에 나온다. 즉 먼저 입력된것이 탑이 된다.
cout << endl;
testQueue.back().print();
//back : return a reference to the last element in vector
//제일 마지막것이 나온다.
while(testQueue.size() > 0)
{
Test &test = testQueue.front();
test.print();
testQueue.pop();
}
return 0;
}
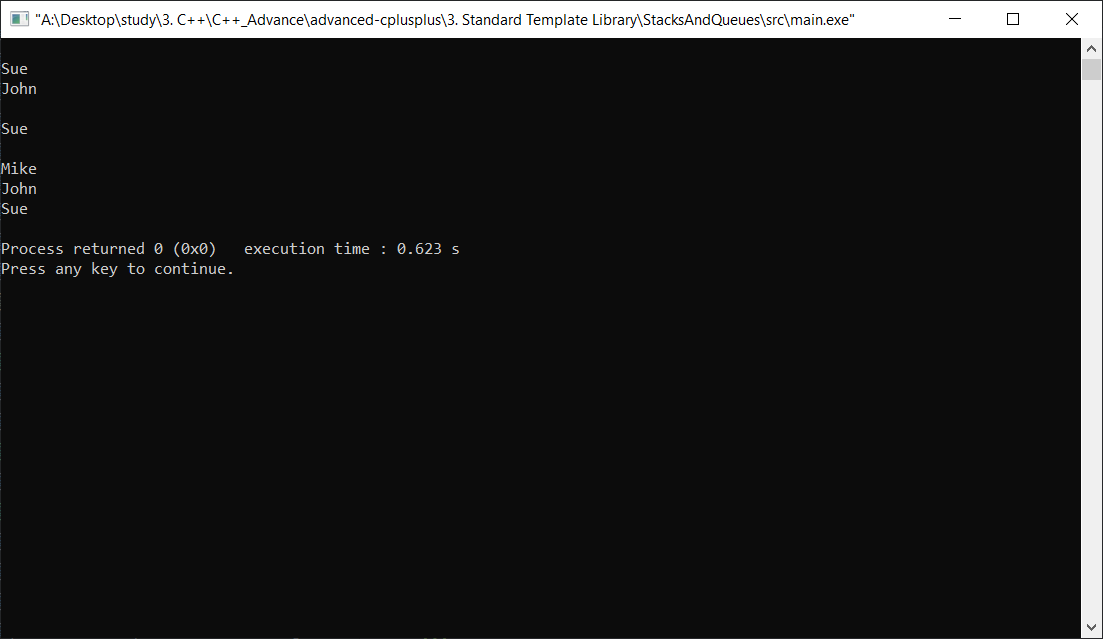
Result
Complex Data
#include <iostream>
#include <string>
#include <vector>
#include <map>
using namespace std;
/**************************************************
*
* Note, some compilers are OK with angle brackets
* used in connection with template types
* being next to each other with no spaces, like
* this: map<string, vector<int>> scores;
* Others require spaces, like this:
* map<string, vector<int> > scores;
* It's safer to put in spaces.
*
**************************************************/
int main() {
map<string, vector<int> > scores;
scores["Mike"].push_back(10);
scores["Mike"].push_back(20);
scores["Vicky"].push_back(15);
for(map<string, vector<int> >::iterator it = scores.begin(); it!= scores.end(); it++)
{
string name = it->first;
vector<int> scoreList = it->second;
cout << name << ": " << flush;
for(int i = 0; i < scoreList.size(); i++)
{
cout << scoreList[i] << " " << flush;
//flush 버퍼 저장하지 않고 바로바로 디스플레이한다/
}
cout << endl;
}
return 0;
}
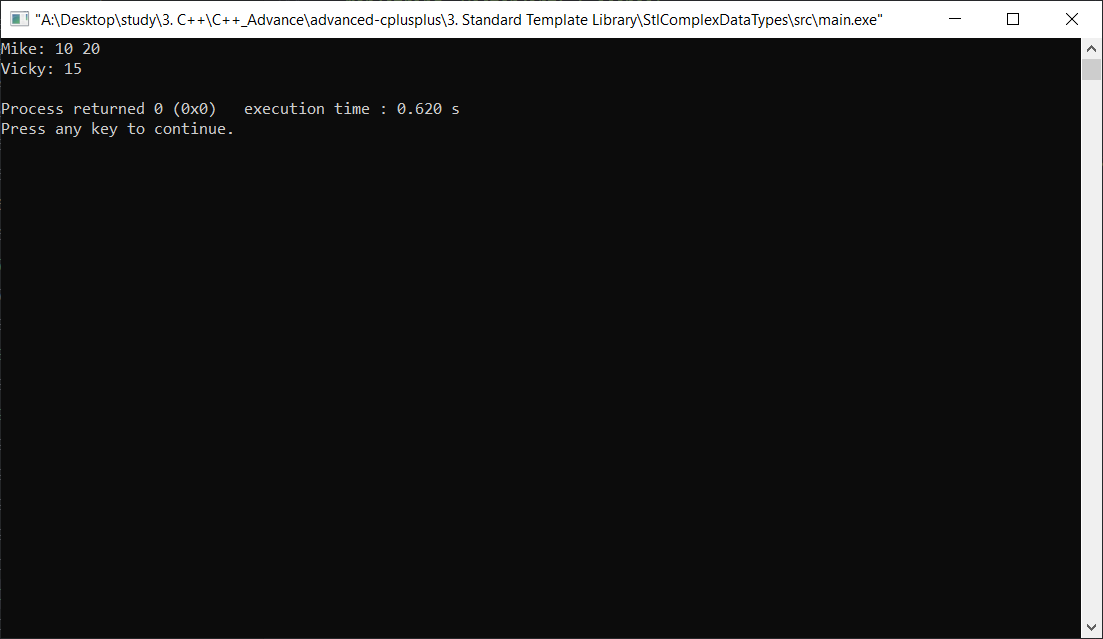
Result
REFERENCE
List
- 리스트(list) 의 경우 양방향 연결 구조를 가진 자료형이라 볼 수 있습니다.

- 따라서 vector 와는 달리 임의의 위치에 있는 원소에 접근을 바로 할 수 없습니다.
- list 컨테이너 자체에서는 시작 원소와 마지막 원소의 위치만을 기억하기 때문에, 임의의 위치에 있는 원소에 접근하기 위해서는 하나씩 링크를 따라가야 합니다.
- 그래서 리스트에는 아예 [] 나 at 함수가 아예 정의되어 있지 않습니다.
- vector 의 경우 맨 뒤를 제외하고는 임의의 위치에 원소를 추가하거나 제거하는 작업이 O(n)O(n) 이였지만 리스트의 경우 O(1)O(1) 으로 매우 빠르게 수행될 수 있습니다.
- 왜냐하면 원하는 위치 앞과 뒤에 있는 링크값만 바꿔주면 되기 때문입니다.
예제
#include <iostream>
#include <list>
int main() {
std::list<int> lst;
lst.push_back(10);
lst.push_back(20);
lst.push_back(30);
lst.push_back(40);
for (std::list<int>::iterator itr = lst.begin(); itr != lst.end(); ++itr) {
std::cout << *itr << std::endl;
}
}
결과
10
20
30
40
- 주의할 점은 리스트의 반복자의 경우 다음과 같은 연산 밖에 수행 할 수 없습니다.
itr++ // itr ++
itr-- // --itr 도 됩니다.
itr + 5 //불가능
- 임의의 위치에 있는 원소를 가리킬 수 없다는 것입니다.
- 반복자는 오직 한 칸 씩 밖에 움직일 수 없습니다.
- 즉, 메모리 상에서 원소들이 연속적으로 존재하지 않을 수 있다는 뜻입니다.
- 반면에 벡터의 경우 메모리 상에서 연속적으로 존재하기 때문에 쉽게 임의의 위치에 있는 원소를 참조할 수 있습니다.
- erase 함수를 이용하여 원하는 위치에 있는 원소를 지울 수 도 있습니다.
- 리스트의 경우는 벡터와는 다르게, 원소를 지워도 반복자가 무효화 되지 않습니다.
- 왜냐하면, 각 원소들의 주소값들은 바뀌지 않기 때문입니다.
Example
- 1번째 배열에 100이 추가가 된다.
#include <iostream>
#include <list>
template <typename T>
void print_list(std::list<T>& lst) {
std::cout << "[ ";
// 전체 리스트를 출력하기 (이 역시 범위 기반 for 문을 쓸 수 있습니다)
for (const auto& elem : lst) {
std::cout << elem << " ";
}
std::cout << "]" << std::endl;
}
int main() {
std::list<int> lst;
lst.push_back(10);
lst.push_back(20);
lst.push_back(30);
lst.push_back(40);
std::cout << "처음 리스트의 상태 " << std::endl;
print_list(lst);
for (std::list<int>::iterator itr = lst.begin(); itr != lst.end(); ++itr) {
// 만일 현재 원소가 20 이라면
// 그 앞에 50 을 집어넣는다.
if (*itr == 20) {
lst.insert(itr, 50);
}
}
std::cout << "값이 20 인 원소 앞에 50 을 추가 " << std::endl;
print_list(lst);
for (std::list<int>::iterator itr = lst.begin(); itr != lst.end(); ++itr) {
// 값이 30 인 원소를 삭제한다.
if (*itr == 30) {
lst.erase(itr);
break;
}
}
std::cout << "값이 30 인 원소를 제거한다" << std::endl;
print_list(lst);
}
Result
처음 리스트의 상태
[ 10 20 30 40 ]
값이 20 인 원소 앞에 50 을 추가
[ 10 50 20 30 40 ]
값이 30 인 원소를 제거한다
[ 10 50 20 40 ]
Stack & Queues
- queue : 리스트 한쪽 끝에서만 삽입과 삭제가 일어나는 스택과 달리 리스트의 한쪽 끝에서는 원소들이 삭제되고 반대쪽 끝에서는 삽입만 가능하게 하는 순서화된 리스트 이다. 선입선출 리스트
- explicit Test(string name) : name(name)
- ex) float number = number1; <- 묵시적 형변환
- ex) float number = (int)number1; <- 명시적 형변환
#include <iostream>
#include <string>
#include <stack>
#include <queue>
using namespace std;
class Test
{
string name;
public:
explicit Test(string name) : name(name)
//묵시적인 타입변환을 하지 않고 명시적으로 타입변환을 하였을 경우에만 사용하겠다라는 뜻.
//ex) float number = number1; <- 묵시적 형변환
//ex) float number = (int)number1; <- 명시적 형변환
{
}
~Test()
{
}
void print() const
{
cout << name << endl;
}
};
int main(int argc, char const *argv[])
{
//LIFO(last in first out)
stack<Test> testStack;
testStack.push(Test("Mike"));
testStack.push(Test("John"));
testStack.push(Test("Sue"));
cout << endl;
/* this is invalid code ! objected destroyed.
Test &test1 = testStack.top();
testStock.pop();
test1.print(); // Reference refers to destroyed objects
*/
Test &test1 = testStack.top();
// reference.
test1.print();
// but original gone but test still have value
// this is last one
// .pop is the return the original.
// pop is object destroyed.(top 에 있는 원소를 삭제)
testStack.pop();
Test &test2 = testStack.top();
test2.print();
// the result is john.
//FIFO(first in first out) stack 이랑 반대라 생각하면 된다.
queue<Test> testQueue;
testQueue.push(Test("Mike"));
testQueue.push(Test("John"));
testQueue.push(Test("Sue"));
//여기서는 슈가 마지막에 나온다. 즉 먼저 입력된것이 탑이 된다.
cout << endl;
testQueue.back().print();
//back : return a reference to the last element in vector
//제일 마지막것이 나온다.
while(testQueue.size() > 0)
{
Test &test = testQueue.front();
test.print();
testQueue.pop();
}
return 0;
}
Result
Complex Data
#include <iostream>
#include <string>
#include <vector>
#include <map>
using namespace std;
/**************************************************
*
* Note, some compilers are OK with angle brackets
* used in connection with template types
* being next to each other with no spaces, like
* this: map<string, vector<int>> scores;
* Others require spaces, like this:
* map<string, vector<int> > scores;
* It's safer to put in spaces.
*
**************************************************/
int main() {
map<string, vector<int> > scores;
scores["Mike"].push_back(10);
scores["Mike"].push_back(20);
scores["Vicky"].push_back(15);
for(map<string, vector<int> >::iterator it = scores.begin(); it!= scores.end(); it++)
{
string name = it->first;
vector<int> scoreList = it->second;
cout << name << ": " << flush;
for(int i = 0; i < scoreList.size(); i++)
{
cout << scoreList[i] << " " << flush;
//flush 버퍼 저장하지 않고 바로바로 디스플레이한다/
}
cout << endl;
}
return 0;
}
Result
REFERENCE