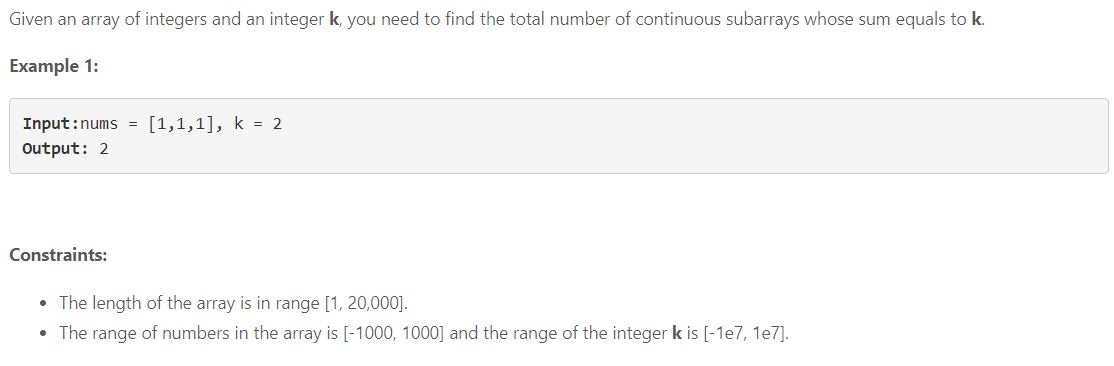
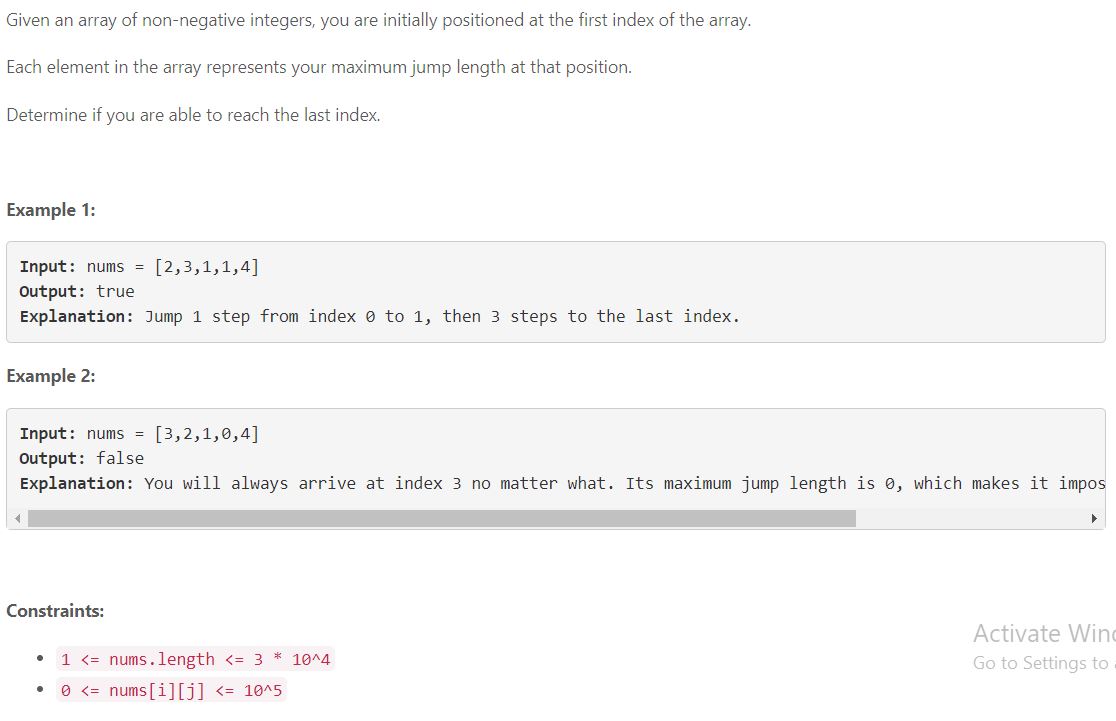
69. Subarray Sum Equals K(헷갈림)
26 Aug 2020 | Daily Algorithms
The approach involves the following:
- Keeping a running sum of all the elements so far as we iterate through them
- If the running sum is equal to k, then we can increment the answer by 1 because then we have found a valid subarray that starts from index 0
- If there is a prefix sum for sum-k in the map, that means we can form sum = k
- This is because the prefix sum for sum subtracted by the the prefix sum for sum-k is k (sum - (sum-k) = k). This means that we can take all of the elements up to sum and subtract it by all of the elements up to sum-k to get k.
- Increase the value in the map for the current running sum
Explanation: we keep an accumulator variable sum with the running total of the sum of numbers; we then check if we have already met that values using our seen hashmap that acts more or less like a frequency table, storing how many times we have encountered a specific value: sum - k.
That is why if have met sum - k before and now the value is sum, the difference between those specific points and the current iteration is, by definiton, exactly k: we are now at sum, so, the interval between the previous point(s) and now sums up to, by definition, sum - (sum - k), which equates k.
We collect all those occurrences in count and finally we return it.
And apparently also the most advanced, reading the solution tab:
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
int sum=0; // calculated sum
unordered_map<int, int> rec; // prefix sum recorder.
int cnt = 0; // number of found subarray
rec[0]++; // to take into account those subrrays that begin with index 0
for(int i = 0; i<nums.size(); i++)
{
sum += nums[i];
cnt += rec[sum-k];
rec[sum]++;
}
return cnt;
}
};
// sum : 1, 2, 3
// cnt : rec[1-2] = 0, rec[2-2] = 1, rec[3-2] = 2
// rec : rec[1] , rec[2], rec[3]
notation
Prefix sum : 어떤 데이터를 누적하여 합한것을 말한다.
The approach involves the following:
- Keeping a running sum of all the elements so far as we iterate through them
- If the running sum is equal to k, then we can increment the answer by 1 because then we have found a valid subarray that starts from index 0
- If there is a prefix sum for sum-k in the map, that means we can form sum = k
- This is because the prefix sum for sum subtracted by the the prefix sum for sum-k is k (sum - (sum-k) = k). This means that we can take all of the elements up to sum and subtract it by all of the elements up to sum-k to get k.
- Increase the value in the map for the current running sum
Explanation: we keep an accumulator variable sum with the running total of the sum of numbers; we then check if we have already met that values using our seen hashmap that acts more or less like a frequency table, storing how many times we have encountered a specific value: sum - k.
That is why if have met sum - k before and now the value is sum, the difference between those specific points and the current iteration is, by definiton, exactly k: we are now at sum, so, the interval between the previous point(s) and now sums up to, by definition, sum - (sum - k), which equates k.
We collect all those occurrences in count and finally we return it.
And apparently also the most advanced, reading the solution tab:
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
int sum=0; // calculated sum
unordered_map<int, int> rec; // prefix sum recorder.
int cnt = 0; // number of found subarray
rec[0]++; // to take into account those subrrays that begin with index 0
for(int i = 0; i<nums.size(); i++)
{
sum += nums[i];
cnt += rec[sum-k];
rec[sum]++;
}
return cnt;
}
};
// sum : 1, 2, 3
// cnt : rec[1-2] = 0, rec[2-2] = 1, rec[3-2] = 2
// rec : rec[1] , rec[2], rec[3]
notation
Prefix sum : 어떤 데이터를 누적하여 합한것을 말한다.