for Robot Artificial Inteligence

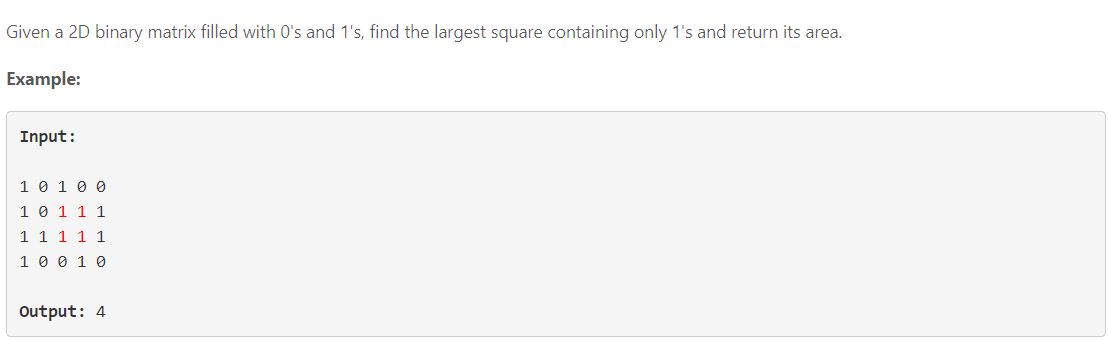
64. Maximal Square [ 어려움 ]

12 Aug 2020 | Daily Algorithms

  • To appy DP, we define the state as the maximal size (square = size * size) of the square that can be formed till point (i, j), denoted as dp[i][j]

  • For the topmost row (i = 0) and the leftmost column (j = 0), we have dp[i][j] = matrix[i][j] - ‘0’, meaning that it can at most form a square of size 1 when the matrix has a ‘1’ in that cell.

  • When i > 0 and j > 0, if matrix[i][j] = ‘0’, then dp[i][j] = 0 since no square will be able to contain the ‘0’ at that cell. If matrix[i][j] = ‘1’, we will have dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1, which means that the square will be limited by its left, upper and upper-left neighbors.
class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if(matrix.empty())
            return 0;
        int m = matrix.size();
        int n = matrix[0].size();
        int sz = 0 ;

        vector<vector<int>> dp(m, vector<int>(n,0));// mxn with elment value 0;
        for(int i = 0; i<m; i++)
        {
            for(int j =0;j<n;j++)
            {
                if(!i || !j || matrix[i][j] == '0')
                {
                    dp[i][j] = matrix[i][j] - '0';
                    // 만약 i와 j가 0일경우 즉 square 테두리 형성과, 스퀘어 안에 0이 있을경우도 square안에 넣음
                }
                else
                {
                  //if matrix[i][j] = '1'
                  // square will be limited by its left, upper and upper-left
                    dp[i][j]= min(dp[i-1][j-1],min(dp[i-1][j],dp[i][j-1]))+1;

                }
                sz = max(dp[i][j],sz);
            }
        }
        return sz*sz;

    }
};

Comment  Read more

63. Binary Tree Maximum Path Sum(난이도 중)

12 Aug 2020 | Daily Algorithms 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    int sum;
public:
    int maxPathSum(TreeNode* root) {
        sum = INT_MIN;
        help(root);
        return sum;
    }

    // return the max-value-ended-at-root-node
    int help(TreeNode* root)
    {
        if(!root)
            return 0;
        int left = max(0,help(root->left));
        int right = max(0,help(root->right));
        // key parts : embedding the max-value-find in the recursion process
        sum = max(sum, left+right+root->val);
        // get the max-value-end-at-root
        return max(left,right)+root->val;
    }
};

Comment  Read more

62. Construct Binary Search Tree from Pre-order Traversal [중간]

30 Jul 2020 | Daily Algorithms

  • Find the left part and right part, then recursively construct the tree.
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* bstFromPreorder(vector<int>& preorder) {
        int i = 0;
        return build(preorder, i, INT_MAX);
    }
    TreeNode* build(vector<int>& A, int& i, int bound)
    {
        if(i == A.size() || A[i]>bound)
            return NULL;
        TreeNode* root = new TreeNode(A[i++]);
        root->left = build(A, i, root->val);
        root->right = build(A, i, bound);
        return root;
    }
};

Comment  Read more

61. Search in Rotated Sorted Array

30 Jul 2020 | Daily Algorithms 

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int i = 0;
        for(auto k : nums)
        {
            i++;
            if(k==target)
                return i-1;
        }
        return -1;

    }
};

Comment  Read more

60. minimum path sums [중간]

30 Jul 2020 | Daily Algorithms

Question Decoration:

  • Consider the matrix as a rectangular plot, and grids as houses
  • Now, you have to go from top-left house to bottom right house
  • Also when you are in some house, you have to pay the rent
  • You can move by only one house at a time, either to Right house or to Down house
  • You have to find the minimum rent to reach the bottom-Right house

Solution:

  • Dynamic Programming(DP)

  • BECAUSE this problem requires optimizing the rent(minimum rent),and at each step we have multiple options, therefore we will use DP steps:

    • Create a dp array of same size as grid
    • dp[0][0] = grid[0][0] , b’coz we are initially in this house
    • dp[i][j] means minimum rent i need to pay to reach the house [i,j]
    • for 0-th row , there is only one way to reach any house, and that is by moving to right, therefore , dp[0][i] = dp[0][i-1] + grid[0][i] (rent paid so far + rent for this house)
    • for 0th column, there is only one way to reach any house, and that is by moving down, therefore, dp[i][0] = dp[i-1][0] + grid[i][0] (rent paid so far + rent for this house)
    • And now for rest of the houses in the grid, say grid[i][j]
      • we can reach either from grid[i-1][j]
      • or from grid[i][j-1]
      • we will choose the one with minimum rent
      • therefore, dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j]
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
    int m = grid.size(); // 행
    int n = grid[0].size(); // 열
    vector<vector<int>> dp(m,vector<int>(n,0)); // m 행의 n 열 with value 0
    dp[0][0] = grid[0][0];
    for(int i=1;i<m;i++)
        dp[i][0] = dp[i-1][0] + grid[i][0];
    for(int j=1;j<n;j++)
        dp[0][j] = dp[0][j-1] + grid[0][j];
    for(int i=1;i<m;i++)
        for(int j=1;j<n;j++)
            dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j];
    return dp[m-1][n-1];
    }
};

Comment  Read more