class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();// 3 x 3
        for(int i = 0; i<n; ++i)
        {
            for(int j=0; j<n;++j)
            {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp
            }
        } // transpose
        for(int i = 0; i<n; ++i)
        {
            for(int j=0; j<(n/2);++j)
            {
                int temp = marix[i][j];
                matrix[i][j] = matrix[i][n-j-1];
                matrix[i][n-j-1] = temp;
            }
        } // flip the matrix horizontally, Fixed 2 colum and change like(1,3)(4,6)(7,9)
    }
};

#include <iostream>
#define V 8
#define I 32767

using namespace std;

void PrintMST(int T[][V-2], int G[V][V]){
    cout << "\nMinimum Spanning Tree Edges (w/ cost)\n" << endl;
    int sum {0};
    for (int i {0}; i<V-2; i++){
        int c = G[T[0][i]][T[1][i]];
        cout << "[" << T[0][i] << "]---[" << T[1][i] << "] cost: " << c << endl;
        sum += c;
    }
    cout << endl;
    cout << "Total cost of MST: " << sum << endl;
}

void PrimsMST(int G[V][V], int n){
    int u;
    int v;
    int min {I};
    int track [V];
    int T[2][V-2] {0};

    // Initial: Find min cost edge
    for (int i {1}; i<V; i++){
        track[i] = I;  // Initialize track array with INFINITY
        for (int j {i}; j<V; j++){
            if (G[i][j] < min){
                min = G[i][j];
                u = i;
                v = j;
            }
        }
    }
    T[0][0] = u;
    T[1][0] = v;
    track[u] = track[v] = 0;

    // Initialize track array to track min cost edges
    for (int i {1}; i<V; i++){
        if (track[i] != 0){
            if (G[i][u] < G[i][v]){
                track[i] = u;
            } else {
                track[i] = v;
            }
        }
    }

    // Repeat
    for (int i {1}; i<n-1; i++){
        int k;
        min = I;
        for (int j {1}; j<V; j++){
            if (track[j] != 0 && G[j][track[j]] < min){
                k = j;
                min = G[j][track[j]];
            }
        }
        T[0][i] = k;
        T[1][i] = track[k];
        track[k] = 0;

        // Update track array to track min cost edges
        for (int j {1}; j<V; j++){
            if (track[j] != 0 && G[j][k] < G[j][track[j]]){
                track[j] = k;
            }
        }
    }
    PrintMST(T, G);
}

int main() {

    int cost [V][V] {
            {I, I, I, I, I, I, I, I},
            {I, I, 25, I, I, I, 5, I},
            {I, 25, I, 12, I, I, I, 10},
            {I, I, 12, I, 8, I, I, I},
            {I, I, I, 8, I, 16, I, 14},
            {I, I, I, I, 16, I, 20, 18},
            {I, 5, I, I, I, 20, I, I},
            {I, I, 10, I, 14, 18, I, I},
    };

    int n = sizeof(cost[0])/sizeof(cost[0][0]) - 1;

    PrimsMST(cost, n);

    return 0;
}

#include <iostream>

#define I 32767  // Infinity
#define V 7  // # of vertices in Graph
#define E 9  // # of edges in Graph

using namespace std;

void PrintMCST(int T[][V-1], int A[][E]){
    cout << "\nMinimum Cost Spanning Tree Edges\n" << endl;
    for (int i {0}; i<V-1; i++){
        cout << "[" << T[0][i] << "]-----[" << T[1][i] << "]" << endl;
    }
    cout << endl;
}

// Set operations: Union and Find
void Union(int u, int v, int s[]){
    if (s[u] < s[v]){
        s[u] += s[v];
        s[v] = u;
    } else {
        s[v] += s[u];
        s[u] = v;
    }
}

int Find(int u, int s[]){
    int x = u;
    int v = 0;

    while (s[x] > 0){
        x = s[x];
    }

    while (u != x){
        v = s[u];
        s[u] = x;
        u = v;
    }
    return x;
}

void KruskalsMCST(int A[3][9]){
    int T[2][V-1];  // Solution array
    int track[E] {0};  // Track edges that are included in solution
    int set[V+1] = {-1, -1, -1, -1, -1, -1, -1, -1};  // Array for finding cycle

    int i {0};
    while (i < V-1){
        int min = I;
        int u {0};
        int v {0};
        int k {0};

        // Find a minimum cost edge
        for (int j {0}; j<E; j++){
            if (track[j] == 0 && A[2][j] < min){
                min = A[2][j];
                u = A[0][j];
                v = A[1][j];
                k = j;
            }
        }

        // Check if the selected min cost edge (u, v) forming a cycle or not
        if (Find(u, set) != Find(v, set)){
            T[0][i] = u;
            T[1][i] = v;

            // Perform union
            Union(Find(u, set), Find(v, set), set);
            i++;
        }
        track[k] = 1;
    }

    PrintMCST(T, A);
}

int main() {
    int edges[3][9] = { 1, 1,  2,  2, 3,  4,  4,  5,  5},
                       { 2, 6,  3,  7, 4,  5,  7,  6,  7},
                       {25, 5, 12, 10, 8, 16, 14, 20, 18}; // {} 이거 더 있어야 한다.

    KruskalsMCST(edges);

    return 0;
}

#include <iostream>
#include <queue>

using namespace std;

void BFS(int vtx, int A[][8], int n){
    queue<int> Q;
    int visited[8] {0};

    // Initial
    cout << vtx << ", " << flush;  // Visit vertex
    visited[vtx] = 1;
    Q.emplace(vtx);

    // Explore
    while (!Q.empty()){
        int u = Q.front();  // Vertex u for exploring
        Q.pop();
        for (int v=1; v<=n; v++){  // Adjacent vertices of vertex u
            if (A[u][v] == 1 && visited[v] == 0){  // Adjacent vertex and not visited
                cout << v << ", " << flush;  // Visit vertex
                visited[v] = 1;
                Q.emplace(v);
            }
        }
    }
    cout << endl;
}

int main (){

    int A[8][8] = {0, 0, 0, 0, 0, 0, 0, 0},
                   {0, 0, 1, 1, 1, 0, 0, 0},
                   {0, 1, 0, 1, 0, 0, 0, 0},
                   {0, 1, 1, 0, 1, 1, 0, 0},
                   {0, 1, 0, 1, 0, 1, 0, 0},
                   {0, 0, 0, 1, 1, 0, 1, 1},
                   {0, 0, 0, 0, 0, 1, 0, 0},
                   {0, 0, 0, 0, 0, 1, 0, 0}; // {} 이거 더있어야 한다

    cout << "Vertex: 1 -> " << flush;
    BFS(1, A, 8);

    cout << "Vertex: 4 -> " << flush;
    BFS(4, A, 8);


    return 0;
}

#include <iostream>
#include <queue>

using namespace std;

void DFS(int u, int A[][8], int n){
    static int visited[8] = {0};
    if(visited[u] == 0)
    {
        cout<< u << ", "<<flush;
        visited[u] = 1;
        for(int v=1; v<n; v++)
        {
            if(A[u][v] == 1 && visited[v]==0)
            {
                DFS(v,A,n);
            }
        }
    }

}

int main (){

    int A[8][8] = {0, 0, 0, 0, 0, 0, 0, 0},
                   {0, 0, 1, 1, 1, 0, 0, 0},
                   {0, 1, 0, 1, 0, 0, 0, 0},
                   {0, 1, 1, 0, 1, 1, 0, 0},
                   {0, 1, 0, 1, 0, 1, 0, 0},
                   {0, 0, 0, 1, 1, 0, 1, 1},
                   {0, 0, 0, 0, 0, 1, 0, 0},
                   {0, 0, 0, 0, 0, 1, 0, 0};// {} 이거 더 있어야 한다.

    cout << "Vertex: 4 -> " << flush;
    DFS(4,A,8);
    cout<<endl;


    return 0;
}

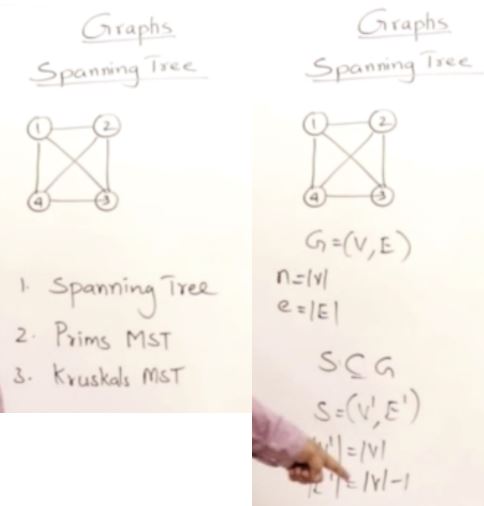
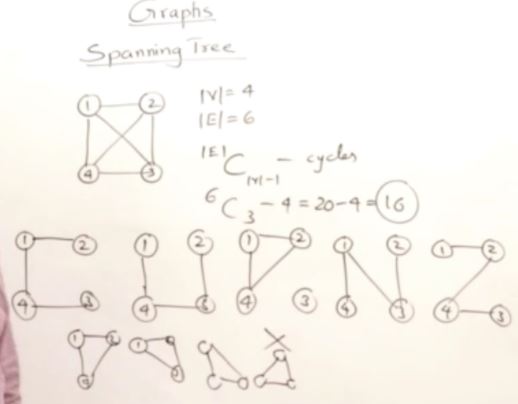
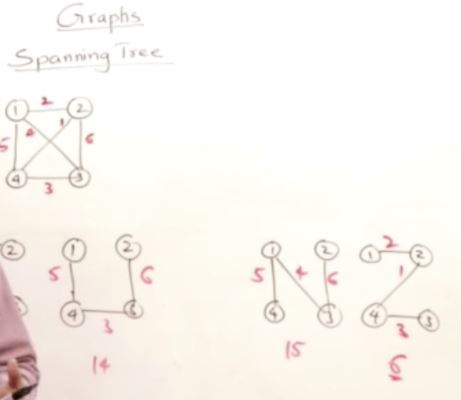
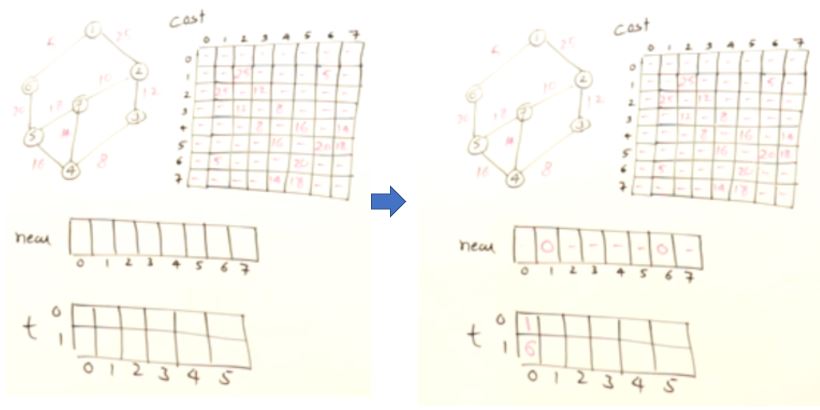
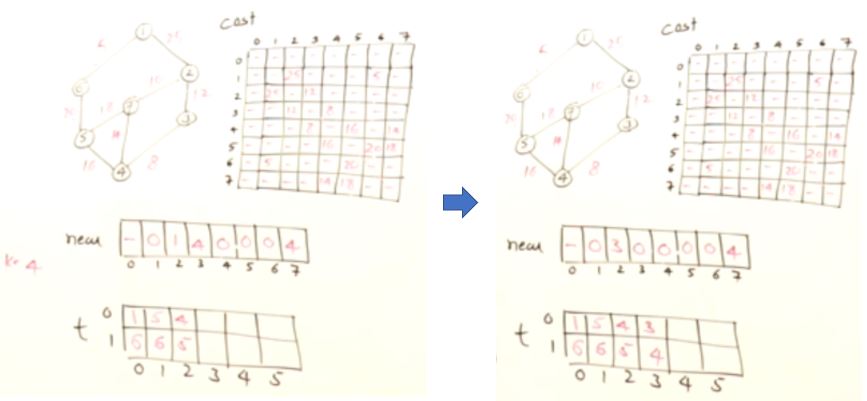
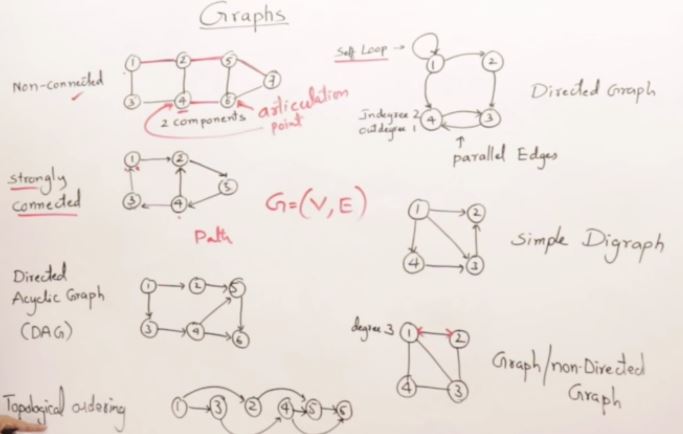
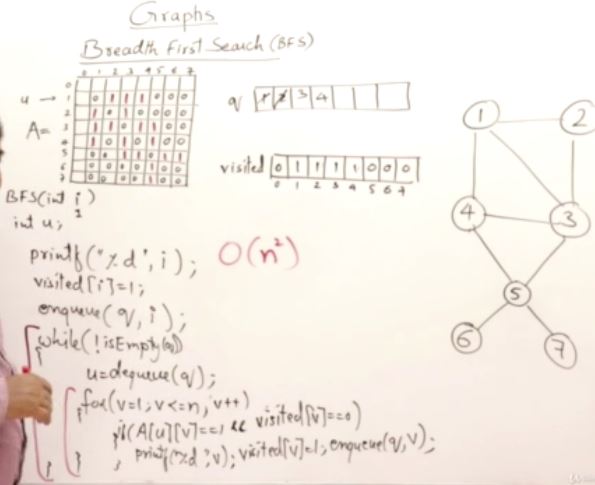
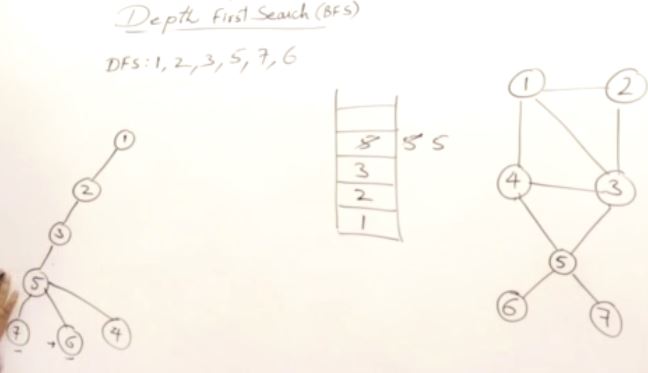
#include <iostream>
#include <stack>

using namespace std;

// Based on Lecture
void DFS(int u, int A[][8], int n){
    // initialize visit tracking array and stack
    int visited[8] = {0};
    stack<int> stk;
    stk.emplace(u);

    // Visit start vertex u
    cout << u << ", " <<flush;
    visited[u] = 1; // visited vertex u

    // initial adjacent vertex
    int v =0;

    while(!stk.empty())
    {
        while(v<n)
        {
            if(A[u][v]==1 && visited[v] == 0)
            {
                stk.push(u); // suspend exploring current vertex u
                u = v;

                //Visit Current vertex u
                cout << u << ", "<<flush;
                visited[u] = 1;
                v = -1; // increment will make this 0
            }
            v++;
        }
        v = u; // can set v= 0; but seeing v=u is better;
        u = stk.top(); //return previous suspsended vertex
        stk.pop();
    }

}

// Simpler and adds elements to stack from end
void dfs(int u, int A[][8], int n)
{
    int visited[8] = {0};
    stack<int> stk;
    stk.emplace(u);

    while(!stk.empty())
    {
        u = stk.top();
        stk.pop();
        if(visited[u]!=1)
        {
            cout<< u << ", "<<flush;
            visited[u] = 1;
            for(int v = n -1; v>=0; v--)
            {
                if(A[u][v]==1 && visited[v]== 0)
                {
                    stk.emplace(v);
                }
            }
        }
    }

}

int main (){

    int A[8][8] = {0, 0, 0, 0, 0, 0, 0, 0},
                   {0, 0, 1, 1, 1, 0, 0, 0},
                   {0, 1, 0, 1, 0, 0, 0, 0},
                   {0, 1, 1, 0, 1, 1, 0, 0},
                   {0, 1, 0, 1, 0, 1, 0, 0},
                   {0, 0, 0, 1, 1, 0, 1, 1},
                   {0, 0, 0, 0, 0, 1, 0, 0},
                   {0, 0, 0, 0, 0, 1, 0, 0}; // {} 이거 더 있어야 한다.
    int u = 5;
    cout << "DFS Vertex: " << u << "-> "<< flush;
    DFS(u,A,8);
    cout<<endl;

    cout << "dfs Vertex: " << u << " -> " << flush;
    dfs(u, A, 8);
    cout<<endl;



    return 0;
}

#include <iostream>
#include <cmath>
using namespace std;

class Node
{
public:
    int data;
    Node* next;
};
class HashTable
{
public:
    Node** HT;
    HashTable();
    ~HashTable();
    void Insert(int key);
    int Hash(int key);
    int Search(int key);
};
int HashTable::Search(int key)
{
    int hldx = Hash(key);
    Node* p = HT[hldx];
    while(p)
    {
        if(p->data == key)
        {
            return p->data;
        }
        else
        {
            p = p->next;
        }
    }
    return -1;
}
int HashTable::Hash(int key)
{
    return key%10;
}
void HashTable::Insert(int key)
{
    int hldx = Hash(key);
    Node* t = new Node;
    t->data = key;
    t->next = nullptr;
    // Case No nodes in the linked list;
    if(HT[hldx] == nullptr)
    {
        HT[hldx] = t;
    }
    else
    {
        Node* p = HT[hldx];
        Node* q = HT[hldx];

        // Traverse to find Insert position
        while(p && p->data < key)
        {
            q = p;
            p = p->next;
        }
        // case Insert position first
        if(q==HT[hldx])
        {
            t->next = HT[hldx];
            HT[hldx] = t;
        }
        else
        {
            t->next = q->next;
            q->next = t;
        }
    }
}
HashTable::HashTable()
{
    HT = new Node*[10];
    for(int i =0; i<10; i++)
    {
        HT[i] = nullptr;
    }
}

HashTable::~HashTable()
{
    for(int i=0; i<10; i++)
    {
        Node* p = HT[i];
        while(HT[i])
        {
            HT[i] = HT[i]->next;
            delete p;
            p = HT[i];
        }
    }
    delete[] HT;
}
int main()
{
    int A[] = {16, 12, 25, 39, 6, 122, 5, 68, 75};
    int n = sizeof(A)/sizeof(A[0]);
    HashTable H;
    for(int i=0; i<n;i++)
    {
        H.Insert(A[i]);
    }
    cout << "Successful Search" << endl;
    int key = 6;
    int value = H.Search(key);
    cout << "Key: " << key << ", Value: " << value << endl;
    cout << "Unsuccessful Search" << endl;
    key = 95;
    value = H.Search(key);
    cout << "Key: " << key << ", Value: " << value << endl;
    return 0;
}

#include <iostream>
#define SIZE 10
using namespace std;
template <class T>
void Print(T& vec, int n, string s)
{
    cout<<s<<": ["<<flush;
    for(int i=0; i<n;i++)
    {
        cout<<vec[i]<<flush;
        if(i<n-1)
        {
            cout<<", " <<flush;
        }
    }
    cout<<"]"<<endl;
}
int Hash(int key)
{
    return key%SIZE;
}
int LinearProbe(int A[],int key)
{
    int idx = Hash(key);
    int i=0;
    while(A[idx+i]%SIZE != 0)
    {
        i++;
    }
    return (idx+i)%SIZE;
}
void Insert(int A[], int key)
{
    int idx = Hash(key);
    if(A[idx!=0])
    {
        idx = LinearProbe(A,key);
    }
    A[idx] = key;
}
int Search(int H[], int key)
{
    int idx = Hash(key);
    int i=0;
    while(H[(idx+i)%SIZE] != key)
    {
        i++;
        if(H[(idx+i)%SIZE] == 0)
            return -1;
    }
    return (idx+i)%SIZE;
}
int main()
{
    int A[] = {26, 30, 45, 23, 25, 43, 74, 19, 29};
    int n = sizeof(A)/sizeof(A[0]);
    Print(A, n, " A");
    // HASH TABLE
    int HT[10] = {0};
    for(int i=0; i<n;i++)
    {
        Insert(HT,A[i]);
    }
    Print(HT, SIZE, "HT");
    int index =Search(HT,25);
    cout << "key found at: " << index << endl;

    index = Search(HT, 35);
    cout << "key found at: " << index << endl;
    return 0;
}

#include <iostream>
#define SIZE 10
using namespace std;
template <class T>
void Print(T& vec, int n, string s)
{
    cout<<s<<": ["<<flush;
    for(int i=0; i<n;i++)
    {
        cout<<vec[i]<<flush;
        if(i<n-1)
        {
            cout<<", " <<flush;
        }
    }
    cout<<"]"<<endl;
}
int Hash(int key)
{
    return key%SIZE;
}
int QuadraticProbe(int A[],int key)
{
    int idx = Hash(key);
    int i=0;
    while(A[idx+i*i]%SIZE != 0)
    {
        i++;
    }
    return (idx+i*i)%SIZE;
}
void Insert(int A[], int key)
{
    int idx = Hash(key);
    if(A[idx!=0])
    {
        idx = QuadraticProbe(A,key);
    }
    A[idx] = key;
}
int Search(int H[], int key)
{
    int idx = Hash(key);
    int i=0;
    while(H[(idx+i*i)%SIZE] != key)
    {
        i++;
        if(H[(idx+i*i)%SIZE] == 0)
            return -1;
    }
    return (idx+i*i)%SIZE;
}
int main()
{
    int A[] = {26, 30, 45, 23, 25, 43, 74, 19, 29};
    int n = sizeof(A)/sizeof(A[0]);
    Print(A, n, " A");
    // HASH TABLE
    int HT[10] = {0};
    for(int i=0; i<n;i++)
    {
        Insert(HT,A[i]);
    }
    Print(HT, SIZE, "HT");
    int index =Search(HT,25);
    cout << "key found at: " << index << endl;

    index = Search(HT, 35);
    cout << "key found at: " << index << endl;
    return 0;
}

#include <iostream>
#define SIZE 10
#define PRIME 7
using namespace std;
template <class T>
void Print(T& vec, int n, string s)
{
    cout<<s<<": ["<<flush;
    for(int i=0; i<n;i++)
    {
        cout<<vec[i]<<flush;
        if(i<n-1)
        {
            cout<<", " <<flush;
        }
    }
    cout<<"]"<<endl;
}
int Hash(int key)
{
    return key%SIZE;
}
int PrimeHash(int key)
{
    return PRIME-(key%PRIME);
}
int DoubleHash(int A[],int key)
{
    int idx = Hash(key);
    int i=0;
    while(A[Hash(idx)+i*PrimeHash(idx)%SIZE] != 0)
    {
        i++;
    }
    return (idx+i*PrimeHash(idx)%SIZE)%SIZE;
}
void Insert(int A[], int key)
{
    int idx = Hash(key);
    if(A[idx!=0])
    {
        idx = DoubleHash(A,key);
    }
    A[idx] = key;
}
int Search(int H[], int key)
{
    int idx = Hash(key);
    int i=0;
    while(H[(Hash(idx)+i*PrimeHash(idx))%SIZE] != key)
    {
        i++;
        if(H[Hash(idx)+i*PrimeHash(idx)%SIZE] == 0)
            return -1;
    }
    return Hash(idx)+i*PrimeHash(idx)%SIZE;
}
int main()
{
    int A[] = {26, 30, 45, 23, 25, 43, 74, 19, 29};
    int n = sizeof(A)/sizeof(A[0]);
    Print(A, n, " A");
    // HASH TABLE
    int HT[10] = {0};
    for(int i=0; i<n;i++)
    {
        Insert(HT,A[i]);
    }
    Print(HT, SIZE, "HT");
    int index =Search(HT,25);
    cout << "key found at: " << index << endl;

    index = Search(HT, 35);
    cout << "key found at: " << index << endl;
    return 0;
}

#include <iostream>

using namespace std;

template<class T>
void Print(T& A, int n, string c)
{
    cout<< c << " : [" <<flush;
    for(int i =0; i < n; i++)
    {
        cout<<A[i]<<flush;
        if(i<n-1)
        {
            cout<<" ,"<<flush;
        }
    }
    cout<<"]" <<endl;
}
void Swap(int* x, int* y)
{
    int temp;
    temp = * x;
    * x = * y;
    * y = temp;
}

void Merge(int A[], int low, int mid, int high)
{
    int i =low;
    int j = mid +1;
    int k = low;
    int B[high+1];
    while(i<mid && j < high)
    {
        if(A[i]<A[j])
        {
            B[k++] = A[i++];
        }
        else
        {
            B[k++] = A[j++];
        }
    }
    while(i<=mid)
    {
        B[k++] = A[i++];
    }
    while(j<=high)
    {
        B[k++] = A[j++];
    }
    for(int i = low; i<=high; i++)
    {
        A[i] = B[i];
    }
}

void IterativeMergeSort(int A[], int n)
{
    int p;
    for(p=2;p<=n;p=p*2)
    {
        for(int i=0; i+p-1<n; i=i+p)
        {
            int low = i;
            int high = i+p-1;
            int mid = (low+high)/2;
            Merge(A, low, mid, high);
        }
    }
    if(p/2<n)
    {
        Merge(A,0,p/2-1,n-1);
    }
}

int main()
{
    int A[] = {2, 5, 8, 12, 3, 6, 7, 10};
    int n = sizeof(A)/sizeof(A[0]);

    Print(A, n, "\t\tA");
    IterativeMergeSort(A, n);
    Print(A, n, "Sorted A");
    return 0;
}

#include <iostream>

using namespace std;

template<class T>
void Print(T& A, int n, string c)
{
    cout<< c << " : [" <<flush;
    for(int i =0; i < n; i++)
    {
        cout<<A[i]<<flush;
        if(i<n-1)
        {
            cout<<" ,"<<flush;
        }
    }
    cout<<"]" <<endl;
}
void Swap(int* x, int* y)
{
    int temp;
    temp = * x;
    * x = * y;
    * y = temp;
}

void Merge(int A[], int low, int mid, int high)
{
    int i =low;
    int j = mid +1;
    int k = low;
    int B[high+1];
    while(i<mid && j < high)
    {
        if(A[i]<A[j])
        {
            B[k++] = A[i++];
        }
        else
        {
            B[k++] = A[j++];
        }
    }
    while(i<=mid)
    {
        B[k++] = A[i++];
    }
    while(j<=high)
    {
        B[k++] = A[j++];
    }
    for(int i = low; i<=high; i++)
    {
        A[i] = B[i];
    }
}

void RecursiveMergeSort(int A[], int low, int high)
{
    if(low<high)
    {
        // Calculate mid point
        int mid = low + (high-low)/2;

        // Sort SUb-lists;
        RecursiveMergeSort(A, low, mid);
        RecursiveMergeSort(A, mid+1, high);

        // Merge Sorted sub-lists;
        Merge(A, low, mid, high);

    }

}

int main()
{
    int A[] = {2, 5, 8, 12, 3, 6, 7, 10};
    int n = sizeof(A)/sizeof(A[0]);

    Print(A, n, "\t\tA");
    RecursiveMergeSort(A,0, n-1);
    Print(A, n, "Sorted A");
    return 0;
}

#include <iostream>

using namespace std;

template<class T>
void Print(T& A, int n, string c)
{
    cout<< c << " : [" <<flush;
    for(int i =0; i < n; i++)
    {
        cout<<A[i]<<flush;
        if(i<n-1)
        {
            cout<<" ,"<<flush;
        }
    }
    cout<<"]" <<endl;
}
int Max(int A[], int n)
{
    int Max_ = -32768; // int min;
    for(int i=0; i<n; i++)
    {
        if(A[i]>Max_)
            Max_ = A[i];
    }
    return Max_;
}
void CountSort(int A[], int n)
{
    int max_ = Max(A,n); //12

    // Create count array
    int* count_ = new int[max_+1]; // making hash table to check the size of index;

    // initilize count array with 0
    for(int i = 0; i< max_+1; i++)
    {
        count_[i] = 0;
    }

    // Update count array values based on A values;
    for(int i = 0; i< n; i++)
    {
        count_[A[i]]++;
    }
    // Update A with sorted elements
    int i = 0;
    int j = 0;
    while(j<max_+1)
    {
        if(count_[j]>0)
        {
            A[i++] = j;
            count_[j]--;
        }
        else
        {
            j++;
        }

    }

    delete[] count_;

}

int main()
{
    int A[] = {2, 5, 8, 12, 3, 6, 7, 10};
    int n = sizeof(A)/sizeof(A[0]);

    Print(A, n, "A");
    CountSort(A,n);
    Print(A, n, "Sorted A");
    return 0;
}

#include <iostream>

using namespace std;

class Node
{
public:
    int value;
    Node* next;
};

template<class T>
void Print(T& A, int n, string c)
{
    cout<< c << " : [" <<flush;
    for(int i =0; i < n; i++)
    {
        cout<<A[i]<<flush;
        if(i<n-1)
        {
            cout<<" ,"<<flush;
        }
    }
    cout<<"]" <<endl;
}
int Max(int A[], int n)
{
    int Max_ = -32768; // int min;
    for(int i=0; i<n; i++)
    {
        if(A[i]>Max_)
            Max_ = A[i];
    }
    return Max_;
}
void Insert(Node** bins, int inx)
{
    Node* temp = new Node;
    temp->value = inx;
    temp->next = nullptr;

    if(bins[inx]==nullptr)
    {
        bins[inx] = temp;
    }
    else
    {
        Node* p = bins[inx];
        while(p->next!=nullptr)
        {
            p=p->next;
        }
        p->next = temp;
    }
}
int Delete(Node** bins, int inx)
{
    Node* p = bins[inx];
    bins[inx] = bins[inx]->next;
    int x = p->value;
    delete p;
    return x;
}
void BinSort(int A[], int n)
{
    int max_ = Max(A,n); //12

    // Create count array
    Node** bins = new Node*[max_+1];// if just use one star here only create a one Node
    // but if we do doulbe star, we can set a size of Node as array in heap memory

    // initilize bin array with 0
    for(int i = 0; i< max_+1; i++)
    {
        bins[i] = nullptr;
    }

    // Update bin array values based on A values;
    for(int i=0; i<n;i++)
    {
        Insert(bins, A[i]);
    }

    // Update A with sorted elements
    int i=0;
    int j=0;
    while(i<max_+1)
    {
        while(bins[i]!=nullptr)
        {
            A[j++] = Delete(bins,i);
        }
        i++;
    }

    delete[] bins;
}

int main()
{
    int A[] = {2, 5, 8, 12, 3, 6, 7, 10};
    int n = sizeof(A)/sizeof(A[0]);

    Print(A, n, "A");
    BinSort(A,n);
    Print(A, n, "Sorted A");
    return 0;
}

#include <iostream>
#include <cmath>
using namespace std;

class Node
{
public:
    int value;
    Node* next;
};

template<class T>
void Print(T& A, int n, string c)
{
    cout<< c << " : [" <<flush;
    for(int i =0; i < n; i++)
    {
        cout<<A[i]<<flush;
        if(i<n-1)
        {
            cout<<" ,"<<flush;
        }
    }
    cout<<"]" <<endl;
}
int Max(int A[], int n)
{
    int Max_ = -32768; // int min;
    for(int i=0; i<n; i++)
    {
        if(A[i]>Max_)
            Max_ = A[i];
    }
    return Max_;
}
void Insert(Node** bins, int value, int inx)
{
    Node* temp = new Node;
    temp->value = value;
    temp->next = nullptr;

    if(bins[inx]==nullptr)
    {
        bins[inx] = temp;
    }
    else
    {
        Node* p = bins[inx];
        while(p->next!=nullptr)
        {
            p=p->next;
        }
        p->next = temp;
    }
}
int Delete(Node** bins, int inx)
{
    Node* p = bins[inx];
    bins[inx] = bins[inx]->next;
    int x = p->value;
    delete p;
    return x;
}
int countDigits(int x)
{
    int count_ =0;
    while(x != 0)
    {
        x = x/10;
        count_ ++;
    }
    return count_;
}
void initializeBins(Node** bins, int n)
{
    for(int i =0; i<n; i++)
    {
        bins[i] = nullptr;
    }
}
int getBinindex(int x, int idx)
{
    return (int)(x/pow(10,idx))%10;
}
void RadixSort(int A[], int n)
{
    int max_ = Max(A,n); //12
    int nPass = countDigits(max_);

    // Create count array
    Node** bins = new Node*[10];// if just use one star here only create a one Node
    // but if we do doulbe star, we can set a size of Node as array in heap memory

    // initilize bin array with 0
    initializeBins(bins,10);

    // Update bin array values based on A values;
    for(int pass = 0; pass<nPass; pass++)
    {
        // Update bins based on A values;
        for(int i=0; i<n; i++)
        {
            int binidx = getBinindex(A[i],pass);
            Insert(bins,A[i],binidx);
        }

        // Update A with sorted elements
        int i=0;
        int j=0;
        while(i<10)
        {
            while(bins[i]!=nullptr)
            {
                A[j++] = Delete(bins,i);
            }
            i++;
        }
        // Initialize bins with nullptr again
        initializeBins(bins, 10);
    }

    delete[] bins;
}

int main()
{
    int A[] = {237, 146, 259, 348, 152, 163, 235, 48, 36, 62};
    int n = sizeof(A)/sizeof(A[0]);

    Print(A, n, "A");
    RadixSort(A,n);
    Print(A, n, "Sorted A");
    return 0;
}

#include <iostream>
#include <cmath>
using namespace std;

template<class T>
void Print(T& A, int n, string c)
{
    cout<< c << " : [" <<flush;
    for(int i =0; i < n; i++)
    {
        cout<<A[i]<<flush;
        if(i<n-1)
        {
            cout<<" ,"<<flush;
        }
    }
    cout<<"]" <<endl;
}

// Code is similar to Insertion Sort with some modifications

void ShellSort(int A[], int n)
{
    for(int gap=n/2; gap>=1; gap/=2)
    {
        for(int j= gap; j<n; j++)
        {
            int temp = A[j];
            int i = j - gap;
            while(i>=0 && A[i]>temp)
            {
                A[i+gap] = A[i];
                i = i-gap;
            }
            A[i+gap] = temp;
        }
    }

}

int main()
{
    int A[] = {11, 13, 7, 12, 16, 9, 24, 5, 10, 3};
    int n = sizeof(A)/sizeof(A[0]);

    Print(A, n, "A");
    ShellSort(A,n);
    Print(A, n, "Sorted A");
    return 0;
}